CP机组改造后其卷取机的折算质量m=29000kg。在式中，，所以，即m的增加也将使得ξh变小，使EPC系统的振荡加剧，稳定性变坏。画出改造后EPC系统的开环幅频伯德图，如图12-18的曲线D所示。改造后的系统的幅值裕量为幅值裕量虽比kSV增大前减少了3.5dB，但仍有12.5dB，满足系统对稳定裕量的要求。......
2023-06-15
CP机组改造后卷取精度预测优化方案
【摘要】：卷取机跑偏EPC控制系统的工作目的就是要保证钢带卷齐的精度。按照现有的文献资料和设计手册中的介绍，钢带卷取时，钢带位移的偏移xi存在一个跑偏频率ωp，只有当EPC系统的频宽ωb大于ωp时，系统才能及时纠偏，这样才能保证卷齐精度。然而，该参数的范围太大，据此进行的设计不够准确，为此，又实测了机组的跑偏频率ωp和纠偏速度vp。
卷取机跑偏EPC控制系统的工作目的就是要保证钢带卷齐的精度。通常要求钢卷边缘卷齐的误差δ≤±1mm。
按照现有的文献资料和设计手册中的介绍，钢带卷取时，钢带位移的偏移xi存在一个跑偏频率ωp，只有当EPC系统的频宽ωb大于ωp时，系统才能及时纠偏，这样才能保证卷齐精度。从物理概念上分析，卷齐精度是稳态误差的对应量，应属于稳态特性，但是要达到要求的卷齐精度，系统自身必须有足够好的动态特性，必须保证ωb大于ωp。
以上分析了改造前和改造后系统的频宽ωb，下面讨论跑偏频率ωp。
据文献介绍，跑偏频率ωp是与卷取速度相对应的，当卷取速度为1m/s时，ωp=0.5～1Hz。然而，该参数的范围太大，据此进行的设计不够准确，为此，又实测了机组的跑偏频率ωp和纠偏速度vp。当卷取速度为40m/min时，测得的跑偏频率ωp=1.5Hz，最大纠偏速度vpmax=1.86cm/s。
显然，这比文献中推荐的参数都大，但是由于改造后EPC系统的频宽ωb=2～2.9Hz，仍满足ωb大于ωp。
EPC系统输出的纠偏位移xo（t）的稳态误差就是卷齐误差δ，它主要由系统对输入指令的稳态误差δ1和系统对干扰信号F（s）的稳态误差δ2组成。
由式（12-1）可得，液压缸-负载环节以F（s）为输入，以X0（s）为输出的干扰传递函数为
以F（s）为输入时，系统的传递系数框图如图12-19所示。
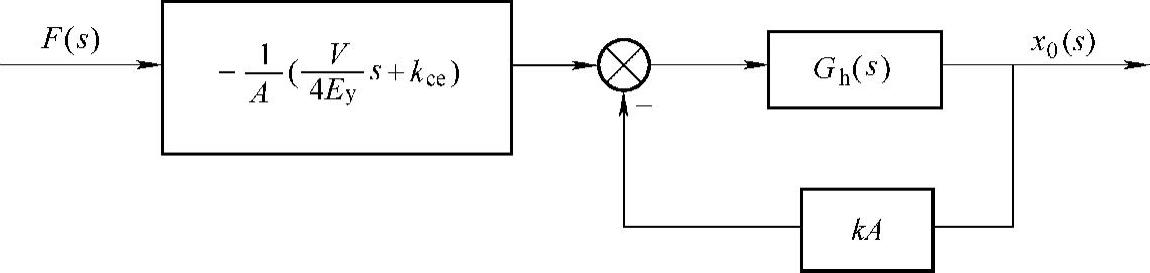
图12-19 系统传递函数框图
整个EPC系统对干扰信号F（s）的闭环传递函数为
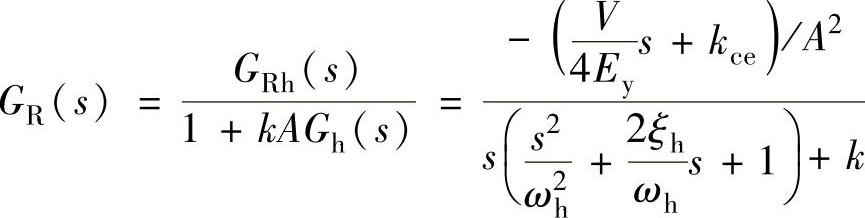
其中负号表示该位移和纠偏位移的方向相反，故是误差量，计算δ2时可将负号省略。
对于常值摩擦力有F（s）=F/s，其中F为干摩擦的稳态值，则：
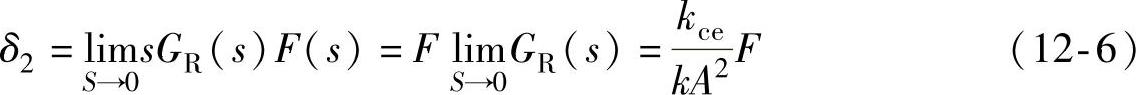
取导轨和液压缸的干摩擦系数u=0.06，则F=uG=0.06×2900×9.8N=1705.2N。又改造后的流量压力系数为改造前的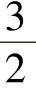
倍，所以有
。取A=3.34×10-2m2，k=18.3，代入式（12-6）得
δ2=0.9×10-5m
实际生产时，由于钢卷在卷筒上的位置不一定对中，所以钢带的张力将有一个沿卷筒轴向的分力，这个力有时将大大超过摩擦力而成为主要的干扰力，所以干扰力引起的卷齐误差往往比计算值大。
EPC系统输入的钢带跑偏位移xi（t）可以认为是等速信号，近似认为跑偏速度等于纠偏速度vp，则xi（t）=vpt，即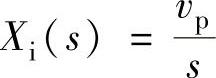
。
实测vp的最大峰值为1.86cm/s，取平均值vp=1.5cm，可得
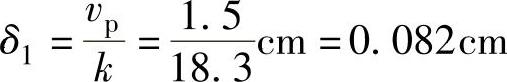
本系统中，伺服阀的零点飘移近似为零，电放大器的精度也相当高，它们引起的误差可忽略，所以总的卷齐误差为
δ=δ1+δ2=0.082cm+0.009cm=0.091cm=0.91mm＜1mm
因此，卷齐误差满足改造对系统的要求。
有关现代冶金设备液压传动与控制的文章
- 详细阅读
-
刀具磨损预测技术优化方案详细阅读
图12-4刀具磨损曲线监测信号的处理分析以及特征的提取是刀具状态监测的关键技术之一。近年来越来越多的学者利用BP神经网络来研究刀具磨损检测技术问题，利用人工神经网络预测刀具磨损是可行的也是科学的。以高速铣削过程中刀具的磨损状态为研究对象，利用刀具在不同磨损状态下的铣削力信号对不同监测技术进行研究，建立了基于BP神经网络预测......
2023-06-28
-
纹理识别精度分析优化方案详细阅读
在表4-2中，其他参与对比的算法的纹理识别精度来自提出这些算法的原始文献以及综述文献[59]。具体来说，在Outex TC-10、KTH-TIPS和CUReT这三个纹理库上，本章方法分别取得了99.95%、99.66%和99.67%的识别精度，位列第一，超过了其他所有参与比较的方法的识别精度；在Outex TC-12、UMD和UIUC这三个纹理库上，本章方法分别取得了99.44%、99.43%和98.80%的识别精度，位列第二，仅次于MRELBP算法在Outex TC-12纹理库和SSLBP算法在UMD、UIUC纹理库上的识别精度。......
2023-06-29
-
卷取机夹送辊液压控制优化方案详细阅读
图9-21 卷取机夹送辊布置结构图带钢到来之前，夹送辊处于辊缝控制模式。此后，正常轧制卷取过程中，控制模式就保持为压力控制模式。当轧机物流跟踪系统跟踪到带尾接近夹送辊时，夹送辊将压力控制模式又切换为辊缝控制模式。图9-22 卷取机夹送辊液压控制回路1—伺服阀 2—换向阀 3—减压阀 4、5—液控单向阀组 6—压力传感器 7—溢流阀-先导电磁阀组......
2023-06-15
-
地铁信号设备故障预测优化方案详细阅读
当信号设备出现故障，后果往往是大面积的列车晚点，严重的故障甚至造成地铁安全性事故。目前各城市的地铁运营公司主要通过设备日常性维修来保证信号设备的稳定性，减少设备出现故障。故障预测系统模型采用BP神经网络来建立，BP神经网络在数据预测方面有其先天优势，可以无限逼近事物的未来趋势。通过实践应用验证了本地铁信号设备故障预测系统的正确性和可用性。......
2023-06-28
-
高精度管材冷拔工艺装备优化方案详细阅读
高精度冷拔管材高精度冷拔材管采用的是等径冷拔，完全避免了管材的强迫缩径，内外壁可以同时加工，克服了普通冷拔的上述缺点，冷拔后管材的组织与性能较好，产品质量更高。......
2023-06-23
- 详细阅读
-
流域污染负荷预测技术优化方案详细阅读
按照0.9的排放率，南沙河流域2020年点源污水量约为20.78万m3/d。非点源污染负荷预测。考虑目前南沙河流域内监测资料较少，本次规划中的非点源污染量计算采用国家环境保护总局下发的《全国水环境容量核定技术指南》提供的输出系数法经验模型，分农业、生活和城市径流污染三方面计算非点源污染负荷，计算方法见式和式。将城市径流和农业污染累加得到一年内非点源污染输入量，南沙河干流年入河COD113.4t以及氨氮22.7t。......
2023-06-26
相关推荐