首页历史故事滞后-超前校正的优化：方法和意义

滞后-超前校正的优化：方法和意义

2023-06-15 历史故事版权反馈

【摘要】：滞后-超前校正环节的传递函数为：滞后-超前校正环节的伯德图如图12-12所示。低频段具有负的斜率和负的相位差，起滞后校正作用。图12-12 滞后-超前校正环节的伯德图图12-13 原系统的开环伯德图1.校正原理低频部分利用校正环节的滞后部分以改善系统的稳态精度。由此即可确定总的滞后-超前校正环节。

滞后-超前校正（先滞后，后超前）是在低频段实施滞后校正，在高频段实施超前校正，综合了两种校正的效果，即先滞后，后超前。滞后-超前校正环节的传递函数为：

滞后-超前校正环节的伯德图如图12-12所示。环节的四个转折频率分别为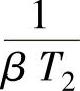、、、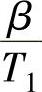。低频段具有负的斜率和负的相位差，起滞后校正作用。高频段具有正的斜率和正相移，起超前校正的作用。伯德图中的几何参数与单独的滞后和超前校正环节相同，最大衰减量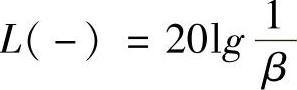，最大超前角φ_m和最大滞后角φ_m（相等）都发生在各自两个转折频率的几何中点。

图12-12 滞后-超前校正环节的伯德图

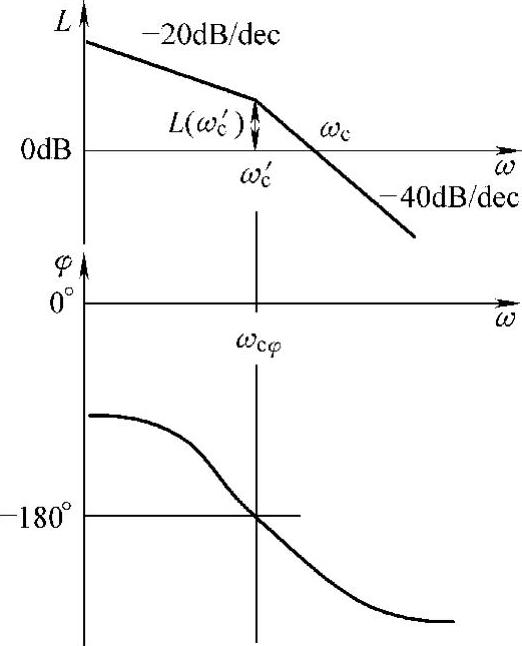
图12-13 原系统的开环伯德图

1.校正原理

低频部分利用校正环节的滞后部分以改善系统的稳态精度。高频部分利用校正环节的超前部分以提高相位裕量而同时又保证足够的频宽。

2.综合滞后校正及超前校正确定校正环节参数的方法

该方法相当于滞后校正及超前校正时参数确定的方法的综合，先按确定超前环节参数α的方法来确定β（β=1/α），再按确定滞后环节转折频率的方法确定T₂。

（1）按稳定误差的要求确定系统的开环放大系数k 根据k及开环传递函数画出原系统的开环伯德图，如图12-13所示。在图中确定相位稳定裕量γ及相频交界频率ω_cφ和幅值裕量h，h=-L（ω_cφ）。

（2）选择校正后系统的幅频剪切频率ω′_c，使得ω′_c=ω_cφ 从理论上讲，校正后系统的相位裕度就应正好等于校正环节在该频率处的相位数。与超前环节相同，为充分利用校正环节和该超前特性，应使该相位数就是校正环节的最大相位超前量φ_m。该方法只适用于原系统完全不稳定，即ω_cφ＜ω_c的系统。

为了补偿计算和作图中发生的误差，应留5°的余量，故φ_m=γ₀+5°，其中γ₀是设计中要求系统达到的相位裕度指标。

（3）由φ_m按下述公式计算β

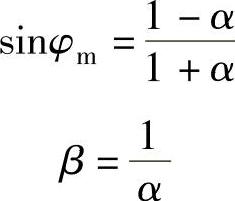
（4）由ω′_c确定T₂ 校正环节滞后部分的第一个转折频率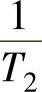（较大者）按下式确定：

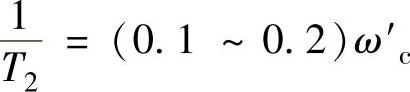
从而校正环节滞后部分的另一转折频率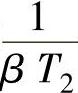也可求得，进而相位滞后部分的传递函数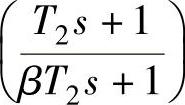即被求得，相位滞后部分的总衰减量。

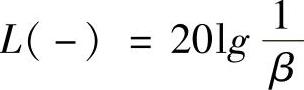（5）校正环节超前部分的两个转折频率可由作图法确定

1）原理：因为校正环节超前部分斜线的斜率为+20dB/dec，由图12-12和图12-13可知，为使校正后的系统稳定，必须使校正环节在ω′_c处的幅值满足L_c（ω′_c）=-L（ω′_c）=-L（ω_cφ）。所以，校正环节超前部分的斜线必过点［ω′_c，-L（ω′_c）］。

2）方法（见图12-12）：在对数坐标纸上先画出滞后部分的幅频曲线，再过点［ω′_c，-L（ω′_c）］作一斜率为+20dB/dec的斜线，该线与0dB线交点的频率即为超前部分的较大的转折频率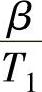，该线与滞后部分下水平线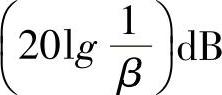线的交点处的频率即为超前部分较小的转折频率。

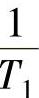由此即可确定总的滞后-超前校正环节。

该校正环节的所有参数全是按系统要求的性能指标来确定的，串联此校正环节后，虽然系统的性能指标得以改善，但是会使系统的阶次增加二次，使系统变得更加复杂，为了克服这一缺点，我们可采取另一种方法来确定校正环节的参数。

3.少增加校正后系统阶次的参数确定方法

1）根据稳态误差的要求，确定系统的开环放大系数k。

2）根据k，绘制未校正系统的对数频率特性，确定其剪切频率ω_c和相位裕度γ。

3）在未校正系统的幅频曲线上选斜率从-20dB/dec变为-40dB/dec的转折频率作为校正环节超前部分较小的那个转折频率（1/T）。

这样选择的好处是：第一，可以使校正后系统的阶次只增加一阶，这是因为校正环节传递函数的分子中将有T₁s+1这一项，而原来系统传递函数的分子中也有T₁s+1这一项，串联后二者可以相消；第二，可保证校正后系统的幅频曲线以-20dB/dec的斜率穿越0dB线，稳定性好；第三，可占据较宽的频带，快速性好。

4）根据对时域响应速度指标的要求，选择校正后系统的剪切频率ω′_c。

①若要求的调整时间小于t_s，要求的相位余量为γ₀，则根据公式

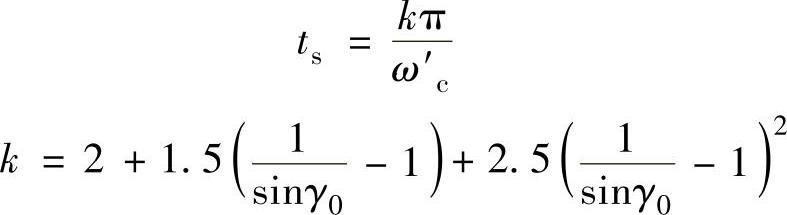
可确定ω′_c，或由图12-14所示曲线可得ω′_c的下限。

图12-14 γ₀、t_s、ω_c关系曲线

②ω′_c的上限应小于未校正系统中幅频曲线的斜率由-40dB/dec向-60dB/dec（或-80dB/dec）转折时的交接频率，这样才能保证校正后的曲线以-20dB/dec的斜率穿越0dB线。

③通常使得ω′_c稍大于下限，能满足调整时间t_s的要求即可。

5）由ω′_c确定β。为了使L（ω′_c）=0，应使校正环节的最大衰减量和原系统在ω′_c处的幅值L（ω′_c）之和等于0，即

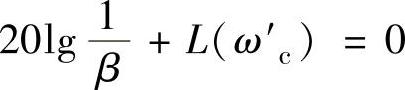
故20lgβ=L（ω′_c）。

6）由已确定的T₁和β写出包含未知参数T₂的校正后系统的传递函数：

校正后系统的频率特性为s→jω，

7）估算确定γ′。若系统要求的相位裕度指标为γ₀，则可取γ′≥γ₀。

8）写出包含未知参数T₂的校正后系统的相角裕度γ′的表达式：

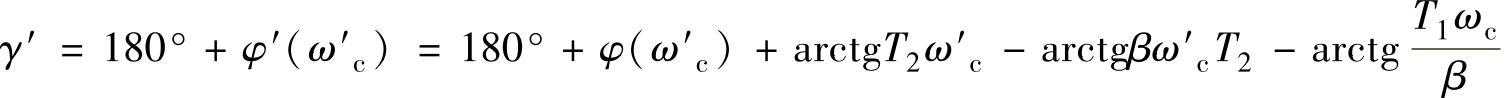
求解此式，即可得T₂，此值是T₂的下限。当然T₂也不可选择过大，否则βT₂更大，过大的时间常数是不容易实现的。由于γ′=180°+φ′（ω′_c），故只要使T₂稍大于下限即可。