首页历史故事积分校正滞后环节优化

积分校正滞后环节优化

2023-06-15 历史故事版权反馈

【摘要】：图12-10 积分校正环节的伯德图积分校正环节的数学模型为，其伯德图如图12-10所示。积分校正环节的参数选择也基于上述原理。6）滞后环节的另一较小的交接频率。

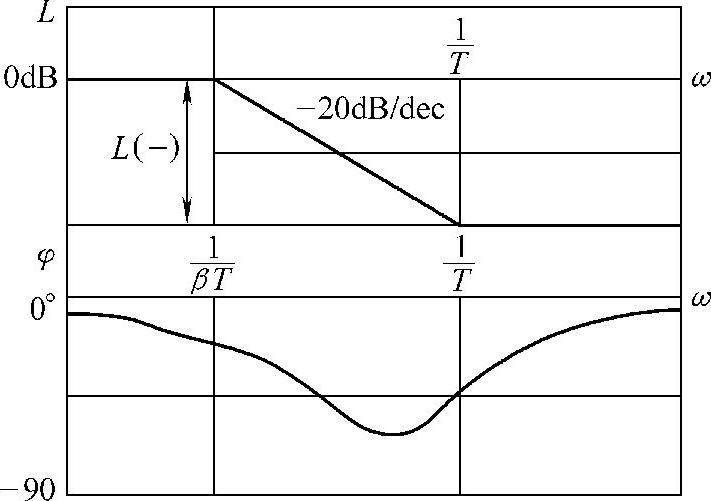
图12-10 积分校正环节的伯德图

积分校正环节的数学模型为（其中，T为时间常数，s为数学模型的自变量，β为衰减系数，β＞1），其伯德图如图12-10所示。校正时利用的是其高频部分幅值衰减的特性。其幅值衰减量为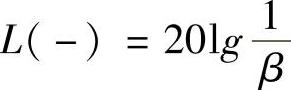，其中β越大，衰减量L（-）的绝对值越大，故β称为衰减系数。

1.校正原理

由于幅值衰减，就可使幅频曲线提前与0dB线相交（使剪切频率减小），这样就增加了相位裕度。当然，还须使得滞后环节的相位滞后区离开剪切频率附近，也就是使得它的两个转折频率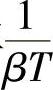、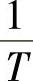都远远小于校正后系统的剪切频率ω′_c，这样剪切频率附近的相位滞后才不致加剧（当然相位滞后总会有少许的），才能保证校正后相位裕度的增加。

积分校正环节的参数选择也基于上述原理。

2.参数确定

确定参数的步骤如下：

1）根据系统稳态误差的要求，确定系统的开环放大系数k。

2）利用已确定的k值，画出未校正的原系统的开环对数频率特性曲线L（ω）和φ（ω），并确定其幅值裕量h和相位裕度γ，若稳定裕量不能满足规定指标，则应加校正。

3）首先找出一个频率点作为系统校正后新的剪切频率ω′_c，ω′_c可在原系统的相频曲线上按下式确定：

φ（ω′_c）=-180°+γ₀+Δφ

式中 γ₀——设计要求的相位裕度指标；

Δφ——为了补偿，加入校正后，滞后环节总会引起的（滞后峰值可以避

开，但不能一点没有）附加的相位滞后，Δφ=5°～12°。

4）确定滞后环节的较大的那个交接频率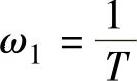，使得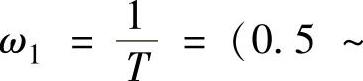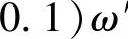，即可确定T（Δφ取大值时，系数取大值）。

5）在原幅频曲线L（ω）上找出ω′_c点的幅值L（ω′_c）；为了使该ω′_c的幅值在校正后为0dB（即成为校正后的剪切频率ω′_c），必须有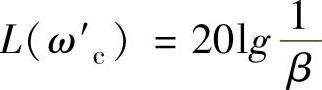，由此即可确定β。

6）滞后环节的另一较小的交接频率。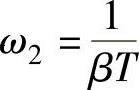

这样，滞后环节的参数就全部确定了。

符号说明：符号“′”代表校正后系统的参数，如φ′、L′、ω′_c分别代表校正后系统的相频、幅频和剪切频率。