首页 历史故事小孔与间隙的流动特性

小孔与间隙的流动特性

2023-06-15 历史故事 版权反馈
【摘要】：在液压传动系统中常遇到油液流经小孔或间隙的情况，如节流阀中的节流小孔及液压元件相对运动表面间的各种间隙。研究液体流经这些小孔和间隙的流量压力特性，对于研究节流调速性能、计算泄漏都是很重要的。上、下两平板均固定不动，液体在间隙两端的压差的作用下而在间隙中流动，称为压差流动。2）两平行平板有相对运动无压差时的间隙流动。

在液压传动系统中常遇到油液流经小孔或间隙的情况，如节流阀中的节流小孔及液压元件相对运动表面间的各种间隙。研究液体流经这些小孔和间隙的流量压力特性，对于研究节流调速性能、计算泄漏都是很重要的。

1.小孔流动

液体流经小孔的情况可以根据孔长l与孔径d的比值分为三种情况：l/d≤0.5时，称为薄壁小孔；0.5＜l/d≤4时，称为短孔；l/d＞4时，称为细长孔。

（1）液流流经薄壁小孔的流量 液体流经薄壁小孔的情况如图1-17所示。液流在小孔上游大约d/2处开始加速并从四周流向小孔。由于流线不能突然转折到与管轴线平行，在液体惯性的作用下，外层流线逐渐向管轴方向收缩，逐渐过渡到与管轴线方向平行，从而形成收缩截面Ac。对于圆孔，约在小孔下游d/2处完成收缩。通常把最小收缩面积Ac与孔口截面积之比值称为收缩系数Cc，即Cc=Ac/A。其中A为小孔的通流截面积。

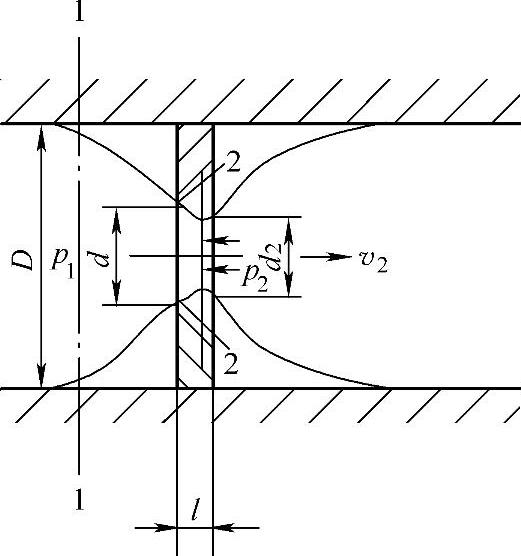
978-7-111-53530-0-Chapter01-81.jpg

图1-17 液体在薄壁小孔中的流动

液流收缩的程度取决于Re、孔口及边缘形状、孔口离管道内壁的距离等因素。对于圆形小孔，当管道直径D与小孔直径d之比D/d≥7时，流速的收缩作用不受管壁的影响，称为完全收缩。反之，管壁对收缩程度有影响时，则称为不完全收缩。

对于图1-17所示的通过薄壁小孔的液流，取截面1-1和2-2为计算截面，设截面1-1处的压力和平均速度分别为p1、v1，截面2-2处的压力和平均速度分别为p2、v2。由于选轴线为参考基准，则Z1=Z2，列伯努利方程为

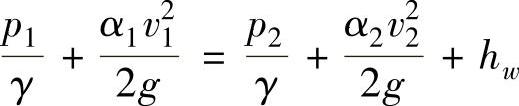
978-7-111-53530-0-Chapter01-82.jpg

由于小孔前管道的通流截面积A1比小孔的通流截面积A大得多，故v1﹤﹤v2，v1可忽略不计。此外，式中的hw部分主要是局部压力损失，由于2-2通流截面取在最小收缩截面处，所以它只有管道突然收缩而引起的压力损失。hw按下式计算：

hw=ζv22/2g

将上式代入伯努利方程中，并令Δp=p1-p2，求得液体流经薄壁小孔的平均速度v2为

978-7-111-53530-0-Chapter01-83.jpg

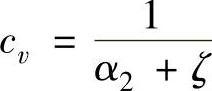令978-7-111-53530-0-Chapter01-84.jpg（cv为小孔流速系数），由于v2是最小收缩截面上的平均速度，设最小通流截面的面积为Ac，与小孔通流截面积A的比值为Ac/A=Cc，则流经小孔的流量为

978-7-111-53530-0-Chapter01-85.jpg

式中 流量系数cd=cvCc；

Δp——小孔前后压差。

流量系数一般由实验确定。在液流完全收缩的情况下，当Re≤105时，cd可按下式计算：

cd=0.964Re－0.05

当Re＞105时，cd可视为常数，取值cd=0.60～0.62。

当液流为不完全收缩时，其流量系数cd≈0.7～0.8。

（2）液流流经细长孔和短孔的流量 液体流经细长小孔时一般都是层流状态，所以可直接应用前面已导出的直管流量式（1-7）来计算。当孔口直径为d时，截面积为A=πd2/4，可写成：

q=πd4Δp/128μl （1-17）

比较式（1-16）和式（1-17）不难发现，通过孔口的流量与孔口的面积、孔口前后的压力差以及孔口形式决定的特性系数有关。由式（1-16）可知，通过薄壁小孔的流量与油液的黏度无关，因此流量受油温变化的影响较小，但流量与孔口前后的压力差呈非线性关系；由式（1-17）可知，油液流经细长小孔的流量与小孔前后的压差Δp呈线性关系，同时由于公式中也包含油液的黏度μ，因此流量受油温变化的影响较大。为了分析问题方便起见，将式（1-16）和式（1-17）一并用式（1-18）表示，即

q=kAΔpm（1-18）

式中 m——指数，当孔口为薄壁小孔时m=0.5，当孔口为细长孔时m=1；

k——孔口的通流系数，当孔口为薄壁孔时978-7-111-53530-0-Chapter01-86.jpg，当孔口为细长

孔时k=d2/32μl。

液流流经短孔的流量仍可套用薄壁小孔的流量计算式：q=cdA（2Δp/ρ）m。由于短孔介于细长孔和薄壁孔之间，故有：0.5＜m＜1，其中特定短孔的流量系数m可在有关液压设计手册中查得。短孔加工比薄壁小孔容易，常用作固定节流器使用。

2.间隙流动

液压元件内各零件间有相对运动，必须要有适当间隙。间隙过大，则会造成泄漏；间隙过小，则会使零件卡死。零件间的泄漏如图1-18所示。泄漏是由压差和间隙造成的。内泄漏的损失转换为热能，使油温升高，外泄漏污染环境，两者均影响系统的性能与效率。因此，研究液体流经间隙的泄漏量、压差与间隙量之间的关系，对提高元件性能及保证系统正常工作是必要的。间隙中的流动一般为层流，一种是压差造成的流动称为压差流动，另一种是相对运动造成的流动称剪切流动，还有一种是在压差与剪切同时作用下的流动。

（1）平行平板的间隙流动 液体流经平行平板间隙的一般情况是既受压差Δp=p1-p2的作用，同时又受到平行平板间相对运动的作用，如图1-19所示。设平板长为l，宽为b（图中未画出），两平行平板间的间隙为h，且l＞＞h，b＞＞h，液体不可压缩，质量力忽略不计，黏度不变。在液体中取一个微元体dx dy（宽度方向取单位长），作用在它与液流相垂直的两个表面上的压力为p和p+dp，作用在它与液流相平行的上下两个表面上的切应力为τ和τ+dτ，因此它的受力平衡方程为

pdy+（τ+dτ）dx=（p+dp）dy+τdx

978-7-111-53530-0-Chapter01-87.jpg

图1-18 内泄漏与外泄漏

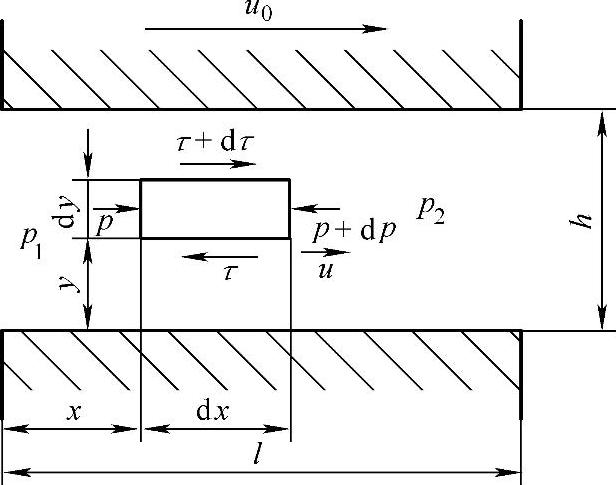
978-7-111-53530-0-Chapter01-88.jpg

图1-19 平行平板间隙流动

经过整理并将液体内摩擦力公式代入后有

978-7-111-53530-0-Chapter01-89.jpg

对上式二次积分可得

978-7-111-53530-0-Chapter01-90.jpg

式中 C1、C2——积分常数。

下面分三种情况进行讨论。

1）固定平行平板间隙流动（压差流动）。上、下两平板均固定不动，液体在间隙两端的压差的作用下而在间隙中流动，称为压差流动。

将边界条件（当y=0时，u=0；当y=h时，u=0）代入式（1-19），得

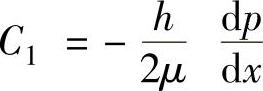
978-7-111-53530-0-Chapter01-91.jpg

C2=0所以

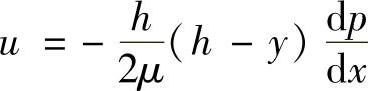
978-7-111-53530-0-Chapter01-92.jpg

于是有

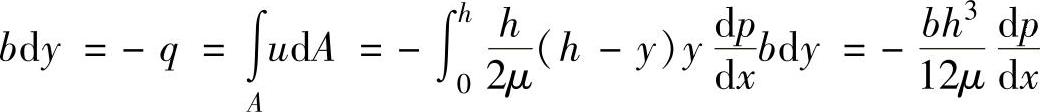
978-7-111-53530-0-Chapter01-93.jpg

因为液流做层流流动时p只是x的线性函数，即

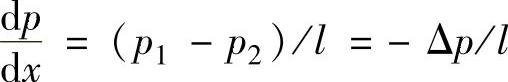
978-7-111-53530-0-Chapter01-94.jpg

将此关系式代入上述流量公式，得

978-7-111-53530-0-Chapter01-95.jpg

从以上两式可以看出，在间隙中的速度分布规律呈抛物线状，通过间隙的流量与间隙的三次方成正比，因此必须严格控制间隙量，以减小泄漏。

2）两平行平板有相对运动无压差时的间隙流动。两平行平板有相对运动，速度为u0，但无压差，这种流动称为纯剪切流动。其流量为

978-7-111-53530-0-Chapter01-96.jpg

3）两平行平板既有相对运动，两端又存在压差时的流动，这是一种普遍情况，其速度和流量是以上两种情况的线性叠加，即

978-7-111-53530-0-Chapter01-97.jpg

式（1-21）中正负号的确定：当长平板相对于短平板的运动方向和压差流动方向一致时，取“+”号；反之取“-”号。

由式（1-21），泄漏所造成的功率损失可写成：

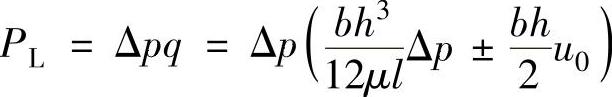
978-7-111-53530-0-Chapter01-98.jpg

由此得出结论：间隙h越小，泄漏功率损失也越小。但是h的减小会使液压元件中的摩擦功率损失增大，因而间隙h有一个使这两种功率损失之和达到最小的最佳值，并不是越小越好。

（2）圆柱环形间隙流动

1）同心环形间隙在压差作用下的流动。图1-20所示为同心环形间隙流动，当h/r＜＜1时，可以将环形间隙间的流动近似地看作是平行平板间隙间的流动，只要将b=πd代入式（1-20），就可得到这种情况下的流动，即

978-7-111-53530-0-Chapter01-99.jpg

该式中“+”号和“-”号的确定同式（1-21）。

2）偏心环形间隙在压差作用下的流动。液压元件中经常出现偏心环状的情况，如活塞与液压缸不同心时就形成了偏向环状间隙。偏心环状间隙中的液流如图1-21所示。R为外圆半径，r为内圆半径，e为环形间隙的偏心距。定义：R-r=h，978-7-111-53530-0-Chapter01-100.jpg（相对偏心量），则偏心环状间隙中的流量（推导从略）为

978-7-111-53530-0-Chapter01-101.jpg

978-7-111-53530-0-Chapter01-102.jpg

图1-20 同心环形间隙间的液流

978-7-111-53530-0-Chapter01-103.jpg

图1-21 偏心环状间隙中的液流

在式（1-23）中，如果ε=0，则相当于同心环形缝隙的情况，这时式（1-23）就变成式（1-22）。如果偏心距达到最大值，即e=h，相当于ε=1，这时由式（1-23）可得通过偏心环形缝隙的最大流量为

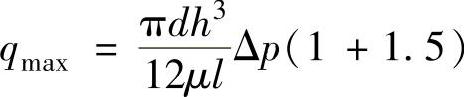
978-7-111-53530-0-Chapter01-104.jpg

即

qmax=2.5q

由上述可知，环形缝隙由于偏心可使泄漏量增大，当偏心最大时，可使泄漏量增大2.5倍。

有关现代冶金设备液压传动与控制的文章

  • 复式河槽水流特性：植被对流动的作用 复式河槽水流特性：植被对流动的作用

    不同的植物对水流的阻力是不同的，总体而言，草对水流的阻力最大。由于复式河槽存在横向动量交换，总体而言，纵向与横向基本上相当，垂向最小。......

    2023-06-22

    详细阅读
  • 液体流经小孔的流量-压力特性分析 液体流经小孔的流量-压力特性分析

    薄壁小孔图1.16 表示液流经过管道的一个薄壁小孔,小孔直径为d。由薄壁小孔流量公式可知,流经薄壁小孔的流量q 与小孔前后压差Δp 的1/2 次方成正比,同时油液流经薄壁小孔时,摩擦阻力作用很小,流量受黏度的影响很小,因而油温变化对流量的影响也很小,此外,薄壁小孔不易堵塞。细长小孔流经细长小孔的液流,由于黏性而流动不畅,故多为层流。......

    2023-06-18

    详细阅读
  • SSDC对直流动态响应特性的影响分析 SSDC对直流动态响应特性的影响分析

    为了考查直流控制系统增加SSDC模块后对直流动态响应性能的影响，本节进行了系统全接线运行方式下的直流电流参考值和直流功率参考值的阶跃动态响应特性的仿真和分析。在呼辽直流输电系统引起的伊敏电厂次同步振荡分析的电磁暂态仿真模型上进行了上述的SSDC对直流动态响应性能的仿真，状态量的阶跃响应如图7-80～图7-87所示。表7-8和表7-9给出了直流控制系统在投入与不投SSDC模块时，HVDC的直流电流、直流功率的阶跃动态响应的主要性能指标。......

    2023-06-22

    详细阅读
  • 装配间隙与偏差控制详解 装配间隙与偏差控制详解

    装配间隙在坡口接头上称根部间隙，是焊前在接头根部之间预留的间隙，须通过装配来保证。因此，必须根据接头坡口准备的实际情况和焊接工艺条件在工艺规程中规定装配间隙的要求。也可以按表9-21提供的在一定板的厚度范围内给出根部间隙的名义尺寸，然后给出偏差值的要求。对于装配件的相互位置偏差，可以根据表9-22提出要求。......

    2023-07-02

    详细阅读
  • 气门间隙检查与调整方法 气门间隙检查与调整方法

    气门间隙是柴油机运行中需要定期检查和调整的重要参数。因此，气门间隙必须进行调整。气门间隙的调整方法 以“双排不进”的调整方法为例进行简要说明。气门间隙的调整步骤 在柴油机完全处于冷态时，才能检查和调整气门间隙。④气门间隙调整结束后，将所有调整螺栓全部拧紧一遍并更换气门室密封垫，然后装上气门室盖，至此，调整结束。......

    2023-09-23

    详细阅读
  • 二冲程发动机扫气过程的端口流动特性及计算 二冲程发动机扫气过程的端口流动特性及计算

    图7-25 二冲程发动机换气过程2.端口流动特性二冲程发动机没有进气门、排气门，仅在气缸壁上设置有进气口、排气口和扫气口，端口根据活塞的位置打开和关闭。图7-26 气缸端口的几何学形状二冲程发动机端口的通道面积随活塞的上下运动（位置）发生变化，因而定义动态流量系数进行相关计算。通过排气口的压力比变化很大，此值在排气减压排放期间大，但在扫气过程期间几乎为1。......

    2023-06-28

    详细阅读
  • 未来工作展望：研究离心泵非定常空化流动特性 未来工作展望：研究离心泵非定常空化流动特性

    因此，今后将在原有试验台的基础上，通过高速全流场显示技术和PIV流场测量技术等研究离心泵内部不同空化阶段的空化流动特性，将试验结果和数值模拟结果进行对比，进一步深入了解离心泵非定常空化流动特性，为实时监测离心泵实际运行中产生的空化提供可靠的依据。......

    2023-06-15

    详细阅读
  • 如何调整导轨副的间隙？ 如何调整导轨副的间隙？

    还可用多规格的薄垫片来调整导轨的间隙。楔形镶条又称楔铁，楔形镶条的全长厚度斜向变化，长的斜度为1∶100、短的斜度为1∶40，且镶条越长斜度越小；依靠调节螺钉使镶条纵向位移来调整导轨的间隙，调整完毕将其固定；其调整容易且受力均匀，但制造较难。......

    2023-06-23

    详细阅读