首页 历史故事圆管中的层流运动及其影响因素

圆管中的层流运动及其影响因素

2023-06-15 历史故事 版权反馈
【摘要】：如图1-13所示，液体在一直径为d的圆管内做层流运动，即Re＜Rexp=2320。图1-13 圆管中的层流在液流中取一小圆柱体，小圆柱体的直径为2y，长度为l，并设液流从左向右流动。

流动状态不同，则流动阻力大小也是不同的，所以还要研究不同的流动状态。

1.流动状态与雷诺数

（1）流动状态——层流和紊流 液体在管道中流动时存在两种不同状态，它们的阻力性质也不相同。

雷诺试验装置如图1-12所示，试验时保持水箱中水位恒定和尽可能平静，然后将阀门A微微开启，使少量水流流经玻璃管，即玻璃管内平均流速v很小。这时，如果将颜色水容器的阀门B也微微开启，使颜色水也流入玻璃管内，我们可以在玻璃管内看到一条细直而鲜明的颜色流束，而且不论颜色水放在玻璃管内的任何位置，它都能呈直线状，这说明管中水流都是安定地沿轴向运动，液体质点没有垂直于主流方向的横向运动，所以颜色水和周围的液体没有混杂，液流按层运动。如果把A阀缓慢开大，管中流量和它的平均流速v也将逐渐增大，直至平均流速增大至某一数值，颜色流束开始弯曲颤动，这说明玻璃管内液体质点不再保持安定，开始发生脉动，不仅具有横向的脉动速度，而且也具有纵向脉动速度。如果A阀继续开大，脉动加剧，颜色水就完全与周围液体混杂而不再维持原来按层运动的状态。

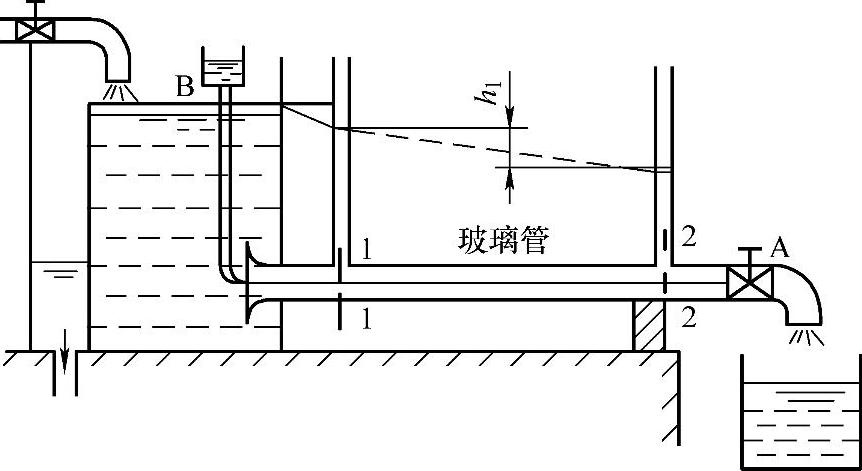
978-7-111-53530-0-Chapter01-47.jpg

图1-12 雷诺试验装置

层流：在液体运动时，如果质点没有横向脉动，不引起液体质点混杂，而是层次分明，能够维持安定的流束状态，这种流动称为层流。

紊流：如果液体流动时质点具有异向脉动，引起流层间质点相互错杂，这种流动称为紊流或湍流。

（2）雷诺数 实验证明，由层流状态转变为紊流状态的流速要比由紊流状态转变为层流状态的流速大得多。我们把从层流状态转变为紊流状态时的流速叫作上临界流速，用v′kp表示，而把从紊流状态转变为层流状态时的流速叫作下临界流速，用vkp表示。液体在圆管中的流动状态不仅与管内的平均流速v有关，还和管径d、液体的运动黏度ν有关。决定液流状态的，是这三个参数所组成的一个称为雷诺数Re的无量纲数，即

978-7-111-53530-0-Chapter01-48.jpg

液体流动时究竟是层流还是紊流，须用雷诺数来判别。液流的雷诺数相同，它的流动状态也相同。相应于上临界流速v′kp的雷诺数，叫作上临界雷诺数；相应于下临界流速vkp的雷诺数，叫作下临界雷诺数。试验指出，虽然在不同管径、不同液体运动黏度时的临界流速vkp、v′kp是不同的，但它的临界雷诺数却有一定的数值界限。金属圆管中液流的下临界雷诺数为

978-7-111-53530-0-Chapter01-49.jpg

当液流的雷诺数Re小于下临界雷诺数时，液流为层流；反之，液流大多为紊流。

2.液体流动时的沿程压力损失

液体在直管中流动时的压力损失是由液体流动时的摩擦引起的，称之为沿程压力损失。它主要取决于管路的长度和内径、液体的流速和黏度等。液体的流态不同，沿程压力损失也不同。

（1）层流时的压力损失和流量 在液压传动中，液体的流动状态多数是层流流动。如图1-13所示，液体在一直径为d的圆管内做层流运动，即Re＜Rexp=2320。

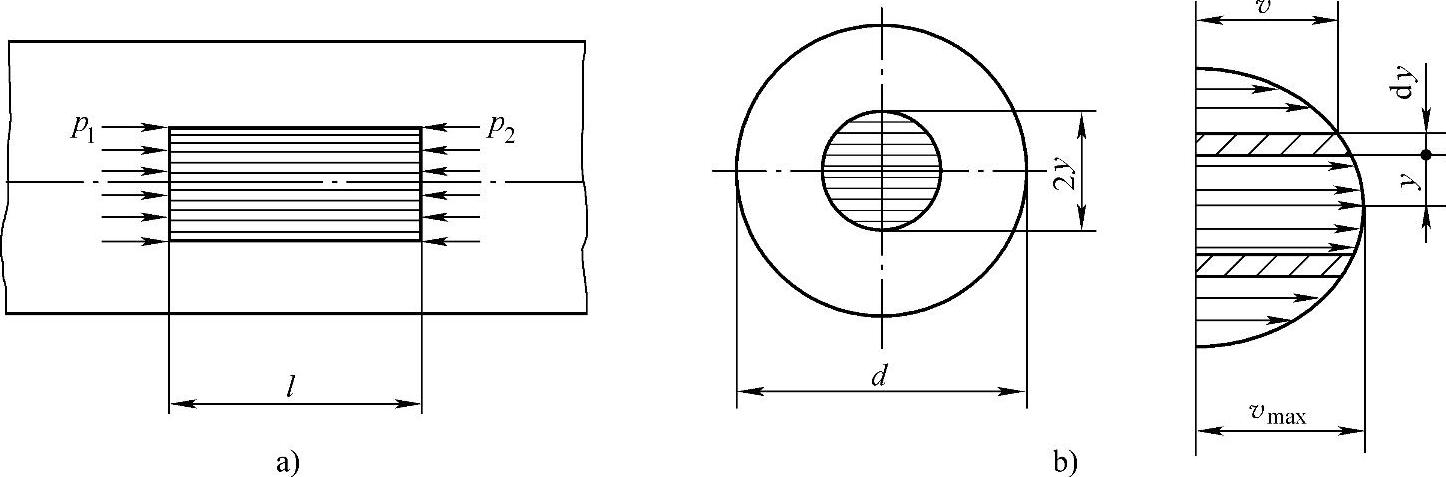
978-7-111-53530-0-Chapter01-50.jpg

图1-13 圆管中的层流

在液流中取一小圆柱体，小圆柱体的直径为2y，长度为l，并设液流从左向右流动。左端的油压力为p1，右端的油压力为p2，由于p1＞p2，故圆柱体所受向右作用力F1为

F1=（p1-p2）πy2

液体在圆管中流动时，由于液体具有黏性，因此在不同半径的各同心圆处液体的流速也不同，圆管中心流速最高，管壁处流速为零，速度分布呈抛物线体形状。由于各液流层之间有速度差，因此流层之间作用有摩擦力T。如前所述（参见本章1.1.6节），此摩擦力与接触面积S、速度梯度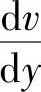978-7-111-53530-0-Chapter01-51.jpg成正比。在图1-13b所示坐标系中，速度随着y的增加而减小，为使摩擦力计算值为正，故在牛顿内摩擦力公式中加了负号，即

978-7-111-53530-0-Chapter01-52.jpg

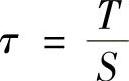切应力978-7-111-53530-0-Chapter01-53.jpg，则

978-7-111-53530-0-Chapter01-54.jpg

因此，图1-13a中，小圆柱体的外表面上所受的向左的作用力F2为

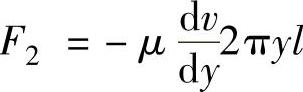
978-7-111-53530-0-Chapter01-55.jpg

F1和F2两力应当互相平衡，即

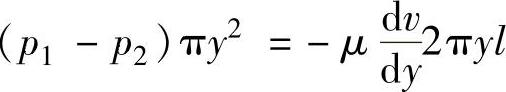
978-7-111-53530-0-Chapter01-56.jpg

或

978-7-111-53530-0-Chapter01-57.jpg

对上式进行积分，得

978-7-111-53530-0-Chapter01-58.jpg

因为在管壁处的流速为零，即978-7-111-53530-0-Chapter01-59.jpg时v=0，所以利用此边界条件，从式（1-5）可求得积分常数978-7-111-53530-0-Chapter01-60.jpg。将积分常数C代入式（1-5），可得管中流速的表达式为

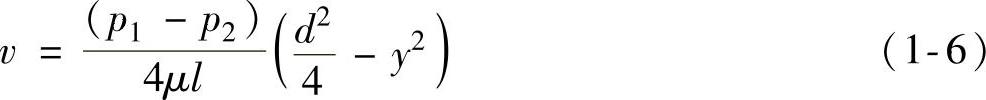
978-7-111-53530-0-Chapter01-61.jpg

管中心，即y=0处，流速最大，其值为

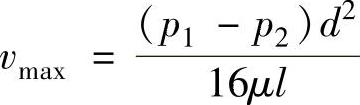
978-7-111-53530-0-Chapter01-62.jpg

从式（1-6）可知，液体在直管中做层流运动时，其速度分布呈抛物线体形状，如图1-13b所示。

下面讨论管中的流量，液体流经直管的流量q就是图1-13b所表示的抛物线体的体积，因此：

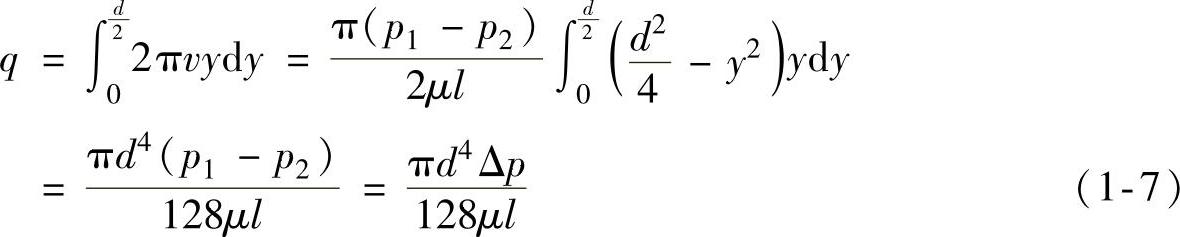
978-7-111-53530-0-Chapter01-63.jpg

从式（1-7）可得层流时直管中沿程压力损失Δp为

978-7-111-53530-0-Chapter01-64.jpg

从式（1-8）可知，层流时沿程压力损失与流速及管长成正比，与管径的平方成反比。

式（1-7）和式（1-8）中各参数的单位应取得一致，如果采用常用单位，并将液体的黏度改用运动黏度，则可得

978-7-111-53530-0-Chapter01-65.jpg

及

978-7-111-53530-0-Chapter01-66.jpg

式中 q——流经直管的流量（l/min）；

d——直管的内径（m）；

γ——液体的重度（N/m3）；

ν——液体的运动黏度（m2/s）；

Δp——直管中沿程压力损失（Pa）；

l——直管的长度（m）。

从式（1-8）可求得液流平均速度v平均为

978-7-111-53530-0-Chapter01-67.jpg

将式（1-11）与最大流速式比较，可得

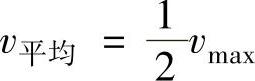
978-7-111-53530-0-Chapter01-68.jpg

在实际计算中，为了简化起见，常将式（1-10）改写成下面将要叙述到的紊流沿程压力损失公式的形式，即

978-7-111-53530-0-Chapter01-69.jpg

式中 λ——沿程压力损失系数；

v——液体的平均流速（m/s）；

g——重力加速度（m/s2）；

Δpλ——沿程压力损失（Pa）。

其他各参数的单位与式（1-10）中的相同。

将式（1-12）和式（1-8）对比，可得式（1-12）中的阻力系数λ相当于：

978-7-111-53530-0-Chapter01-70.jpg

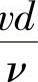而978-7-111-53530-0-Chapter01-71.jpg即相当于雷诺数Re，所以当液体流动状态为层流时，如果用式（1-12）计算压力损失Δpλ，则式中的阻力系数λ为

λ=64/Re （1-14）

在实际计算时，考虑到管子截面可能有收缩和变形，以及靠近管壁的液层有可能冷却，对金属管可取λ=75/Re，对橡胶管取λ=80/Re。

式（1-14）中的雷诺数Re可根据式（1-4）式计算。

由式（1-14）可知，沿程阻力系数λ仅与雷诺数Re有关，而与管壁表面粗糙度无关。也就是说，在层流运动时，沿程压力损失Δp与管壁的表面粗糙度无关。

（2）紊流时的压力损失 层流流动中各质点有沿轴向的规则运动，而无横向运动。紊流的重要特性之一是液体各质点不再是有规则的轴向运动，而是在运动过程中互相渗混合脉动。这种极不规则的运动，引起质点间的碰撞，并形成旋涡，使紊流能量损失比层流大得多。

3.局部压力损失

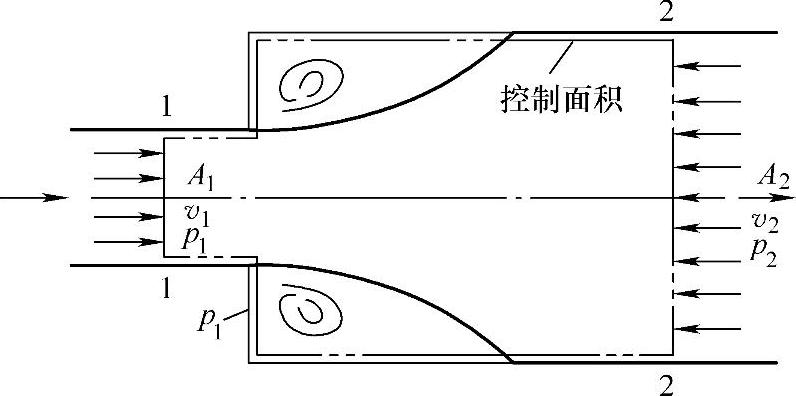
978-7-111-53530-0-Chapter01-72.jpg

图1-14 突然扩大处的局部损失

当液体流动时，除了上述沿程摩擦阻力外，还可能有局部阻力。所谓局部阻力是指液体流过某局部区域时，由于通流面或液流形状的突然改变而引起的阻力，结果造成局部压力损失。例如，液流通过扩大、缩小、转弯等处时，流速要进行重新分布，形成旋涡（见图1-14），使液体质点互相碰撞而消耗能量。这些都是产生局部压力损失的主要原因。

由于液流经过局部阻力区的运动十分复杂，因此只有很少的几种局部压力损失可用理论推导求出，一般均需依靠试验确定。

各种局部压力损失的实质是一样的，普遍的局部压力损失计算公式为

978-7-111-53530-0-Chapter01-73.jpg

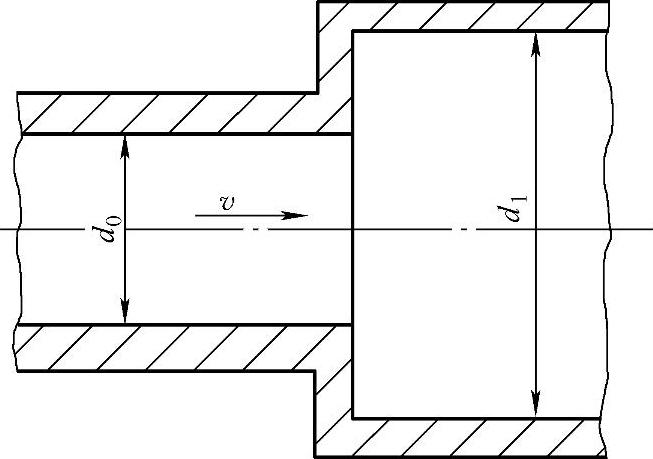
978-7-111-53530-0-Chapter01-74.jpg

图1-15 管道的突然扩大

978-7-111-53530-0-Chapter01-75.jpg

图1-16 管道的突然缩小

几种常见的局部阻力系数ζ的参考数值如下：

（1）管道扩大处的局部阻力系数 管道扩大处的局部阻力系数随管道扩大形式及扩大程度而定。当管道为突然扩大时（见图1-15），ζ随管道直径比值d1/d0变化的数值见表1-2。

（2）管道缩小处的局部阻力系数 管道缩小处的局部阻力系数ζ也是随着管道缩小型式及缩小程度而定。当管道为突然缩小时（见图1-16），ζ随管道直径比值d1/d0变化的数值见表1-3。

表1-2 ζ随d1/d0变化的数值（参考图1-15）

978-7-111-53530-0-Chapter01-76.jpg

表1-3 ζ随d1/d0变化的数值（参考图1-16）

978-7-111-53530-0-Chapter01-77.jpg

（3）阀类元件的局部压力损失 在计算液流经过标准阀类元件的局部压力损失时，可参考该阀在额定流量qh时允许的压力损失Δpζh。但对于压力损失与流量有关的阀类元件，如换向阀、过滤器等，如果通过该阀的实际流量为q，则压力损失Δpζ应按下式计算：

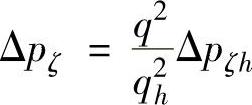
978-7-111-53530-0-Chapter01-78.jpg

4.管路系统中的总压力损失与效率

管路系统的总压力损失Δp总等于所有沿程压力损失和所有局部压力损失之和，即

978-7-111-53530-0-Chapter01-79.jpg

在设计液压系统时，如果液压执行机构（如液压缸等）所需要的有效工作油压为ps，则考虑到系统中的压力损失时，液压泵输出压力应为

pB=ps+Δp总

因此，管路系统的压力效率ηl为

978-7-111-53530-0-Chapter01-80.jpg

管路的压力损失将耗费功率和使油液发热，在设计管路时，应尽量减少液压损失。从前面所介绍的压力损失公式中可看出，在层流中沿程压力损失与流速v成正比，在紊流中沿程压力损失及局部压力损失与速度v的平方成正比，因此为了减少系统中的压力损失，液体在管道中的流速不应过高。但是，流速过低会使管道和阀类元件的尺寸加大，成本增高。

有关现代冶金设备液压传动与控制的文章

  • 圆管内层流运动的流体优化方案 圆管内层流运动的流体优化方案

    图10-5 不可压缩流体在圆管内做均匀层流运动10.5.2 流体流场的速度分布情形圆管层流的最大速度umax为于r=0处，其计算公式为。......

    2023-06-29

    详细阅读
  • 物体运动中形成的阻力及其影响 物体运动中形成的阻力及其影响

    11.6.3 压差阻力物体在流体中运动时因为物体前后压力差引起的阻力称为压差阻力，其形成原因与物体的形状有关，所以压差阻力又称为形状阻力，这里针对其形成原因、影响因素和改善措施描述如下。......

    2023-06-29

    详细阅读
  • 运动竞赛效益评价及其影响因素 运动竞赛效益评价及其影响因素

    运动竞赛效益主要体现在社会效益和经济效益两个方面。运动竞赛的经济效益可以用举办竞赛的投入与举办竞赛的收入的比值来表示。部分运动竞赛之所以有经济效益，是由于运动竞赛具有商品价值。运动竞赛社会效益和经济效益的高低，与竞赛的项目、级别、对象、水平有着密切的关系。......

    2023-11-17

    详细阅读
  • 阻碍发明的因素及其影响 阻碍发明的因素及其影响

    考虑发明的影响因素的时候，阻碍发明进行的因素也不可忽略。吉尔菲兰客观地考察了阻碍发明的一些因素，他们可以分成以下几个方面：一是大组织的标准化问题[39]。发明意味着改变，而改变和标准化相互冲突，所以在标准化生产中，发明的阻力较大。由于产品材料耐久、设计合理，可以长期被人们接受和使用，会自然而然地阻碍新建筑、反对新发明的出现。设备的长久使用在阻止发明方面不仅有直接的影响，还有许多间接后果。......

    2023-11-27

    详细阅读
  • 科幻文学中的新浪潮运动及其影响力 科幻文学中的新浪潮运动及其影响力

    “新浪潮运动”主要发源于英国科幻，而它的影响却波及到世界各地。在这些原因的推动下，科幻小说“新浪潮运动”开始了。这样，从题材到写法，“新浪潮运动”都变革了传统的科幻小说。“新浪潮运动”的名称由此而来。后来他将这段经历写成《太阳帝国》，这是斯皮尔伯格导演的电影《太阳帝国》的剧照“新浪潮运动”的又一位主将是布里安·奥尔迪斯。......

    2024-03-30

    详细阅读
  • 涡流检测及其影响因素 涡流检测及其影响因素

    影响因素多，如裂纹、材质、尺寸、形状及电导率和磁导率等都会影响涡流检测结果。图13-33 涡流检测原理......

    2023-07-02

    详细阅读
  • 呼吸运动的调节及其影响 呼吸运动的调节及其影响

    考点提示呼吸运动的反射性调节。这说明高位脑中枢对节律性呼吸运动的产生不是必需的。目前认为，正常呼吸节律是脑桥和延髓呼吸中枢共同活动形成的。这一反射对正常呼吸运动有一定的调节作用，当支气管痉挛时，引起气道阻力增加，此反射能发挥较明显的作用。通过实验得知，过度通气导致动脉血中PCO2过低时，可发生呼吸运动暂停。实验表明，低氧对呼吸运动的兴奋作用是通过刺激外周化学感受器来实现的。......

    2023-11-02

    详细阅读
  • 影响声腔的因素及其解析 影响声腔的因素及其解析

    俗话说，一方水土养育一方人，一方人受到该地域中各个因素的影响形成一方文化。在日常生活中，“腔”常指语音，且很多情况下指的是地方语音。此处的“腔”指的是一个地方的方言。可见，地方戏曲音乐在流传过程中会受到其他方言的影响而衍生出许多其他相关的流派唱腔。由此不难看出，方言与地方音乐就如方言与声腔的关系，既相互依靠又互相影响。......

    2023-08-25

    详细阅读