流量控制的概念起源于网络通信。我们假设图9-2中Node 4将报文转发到Node 5的速度低于Node 3发送报文的速度。在这种情况下，Node 4将成为整个传送路径上的瓶颈，无论Node 4中的缓存1和2有多大，总会被填满，从而造成节点拥塞。为了避免这类事件发生，网络中的各个组成部件需要对数据传送进行一定的流量控制，合理地接收和发送报文。而流量控制的作用是合理地管理这两类资源，使这些资源能够被有效利用。......
2023-10-20
液体动力学中的流量连续性方程
【摘要】：令此流量与上述实际流量相等，得则平均流速为2.流量连续性方程流量连续性方程是质量守恒定律在流体力学中的一种表达形式。
本节主要讨论三个基本方程式，即液流的连续性方程、伯努利方程和动量方程。它们和刚体力学中的质量守恒、能量守恒及动量守恒原理相对应，都用于描述运动物体的力学特性。液流的连续性方程、伯努力方程描述了压力、流速与流量之间的关系，以及液体能量相互间的变换关系，动量方程描述了流动液体与固体壁面之间作用力的情况。
1.基本概念
（1）理想液体与恒定流动 液体具有黏性，并在流动时表现出来，因此研究流动液体时就要考虑其黏性，而液体的黏性阻力是一个很复杂的问题，这就使我们对流动液体的研究变得复杂。因此，我们引入理想液体和恒定流动的概念。理想液体就是指没有黏性、不可压缩的液体。我们把既具有黏性又可压缩的液体称为实际液体。
液体流动时，若液体中任何一点的压力、速度和密度都不随时间而变化，则这种流动就称为恒定流动（定常流动或非时变流动）。在流体的运动参数中，只要有一个运动参数随时间而变化，液体的运动就是非恒定流动或非恒定流动，如图1-6所示。
（2）通流截面、流量和平均流速
1）通流截面：液体在管道中流动时，其垂直于流动方向的过流断面为通流截面。
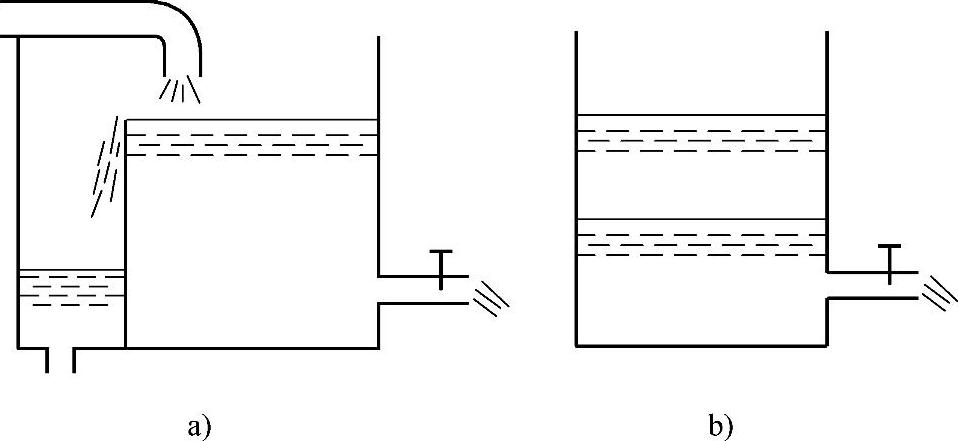
图1-6 液体流动
a）恒定出流 b）非恒定出流
2）流量：单位时间内通过通流截面的液体的体积称为流量，用q表示，流量的常用单位为L/min。
对微小流束，通过dA上的流量为dq，其表达式为dq=udA，在通流截面上积分可得
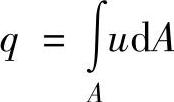
3）平均流速：在实际液体流动中，由于黏性摩擦力的作用，通流截面上流速u的分布规律难以确定，因此引入平均流速的概念，即认为通流截面上各点的流速均为平均流速，用v来表示，则通过通流截面的流量就等于平均流速乘以通流截面积。令此流量与上述实际流量相等，得
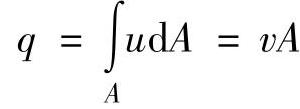
则平均流速为
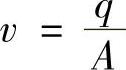
2.流量连续性方程
流量连续性方程是质量守恒定律在流体力学中的一种表达形式。在如图1-7所示的流体中，任选两个通流截面A1和A2，则不可压缩流体做恒定流动的连续性方程为
v1A1=v2A2
由于通流截面是任意取的，则有
q=v1A1=v2A2=v3A3=……=vnAn=常数
式中 v1、v2——分别是流管通流截面A1及A2上的平均流速。
此式表明通过流管内任一通流截面上的流量相等。当流量一定时，任一通流截面上的通流面积与流速成反比，则有任一通流断面上的平均流速为
vi=q/Ai
3.伯努利方程
伯努利方程是能量守恒定律在流体中的一种表达形式。
（1）理想流体的伯努利方程 为研究的方便，一般将液体作为没有黏性摩擦力的理想流体来处理。理想流体的能量在流动中应该守恒，故对于单位重量理想流体有
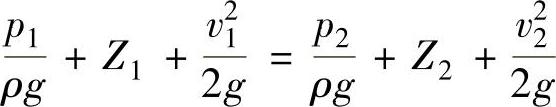
式中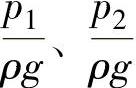 
——单位重量液体所具有
的压力能；
Z1、Z2——单位重量液体所具有的势能；
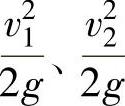——单位重量液体所具有的动能，它们的量纲都为长度，下标1和2分别代表流动中上下游位置通流断面的序号，如图1-8所示。
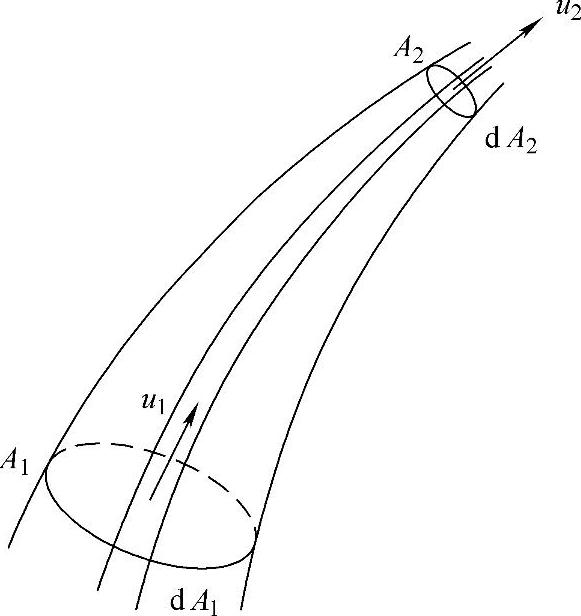
图1-7 流量连续性示意图
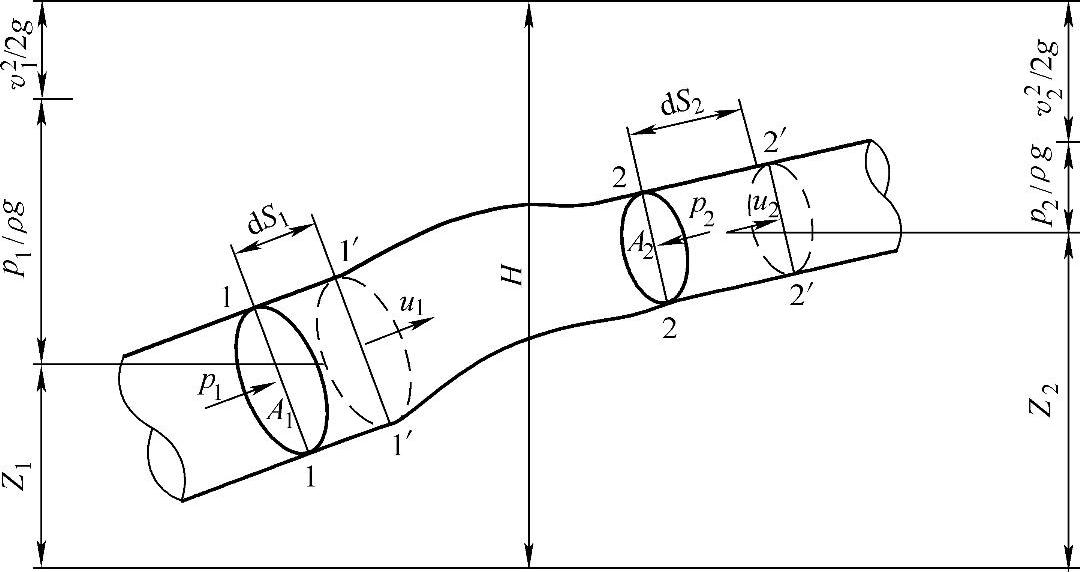
图1-8 液流伯努利方程的能量关系转换图
伯努利方程的物理意义为：在密封管道内做恒定流动的理想液体在任意一个通流断面上具有三种形成的能量，即压力能、势能和动能。三种能量的总和是一个恒定的常量，而且三种能量之间是可以相互转换的，即在不同的通流断面上，同一种能量的值会是不同的，但各断面上的总能量值都是相同的。
（2）实际液体的伯努利方程 由于液体存在着黏性，并表现为对液体流动的阻力，实际液体的流动要克服这些阻力，表示为机械能的消耗和损失，因此当液体流动时，液流的总能量或总比能在不断地减少。所以，实际液体的伯努力方程为
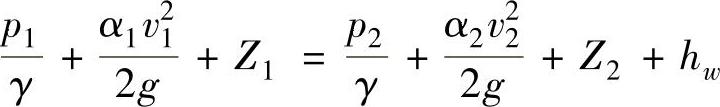
式中 α1、α2——分别为两个通流截面处的动能修正系数，紊流流动时可将动能修正系数取为1；
hw——两个通流截面之间机械能的消耗和损失。
应用伯努利方程式来解决实际问题时必须满足以下的限制条件：
1）液体的流动是稳定流动，即流过空间某一固定点的液体质点的速度、压力不随时间而变化。
2）所选择的两个通流面必须符合渐变流条件，至于在两个通流面之间的水流，可以是渐变流，也可以是急变流。所谓渐变流是一种流线几乎是平行的直线运动。液体在渐变流时，通流面可近似地看作是平面，在同一通流面上各点的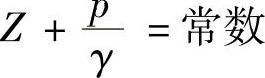
，这是因为在渐变流时在液流的垂直方向上没有液体流动，故在液流的垂直方向上不存在摩擦阻力。
3）液体所受的力只是压力与重力（忽略惯性力的影响）。
4）液体是连续的、不可压缩的，即密度ρ=常数。
例：伯努利方程式在安全阀流量计算中的具体应用。
液压系统中，当液压油的压力超过安全阀的弹簧力时，安全阀就打开，油液经此而流回油箱。压力越大，打开的通道截面越大，通过安全阀的流量也就越大。但是它们之间到底是一个什么样的数量关系呢？下面就来分析这个问题。
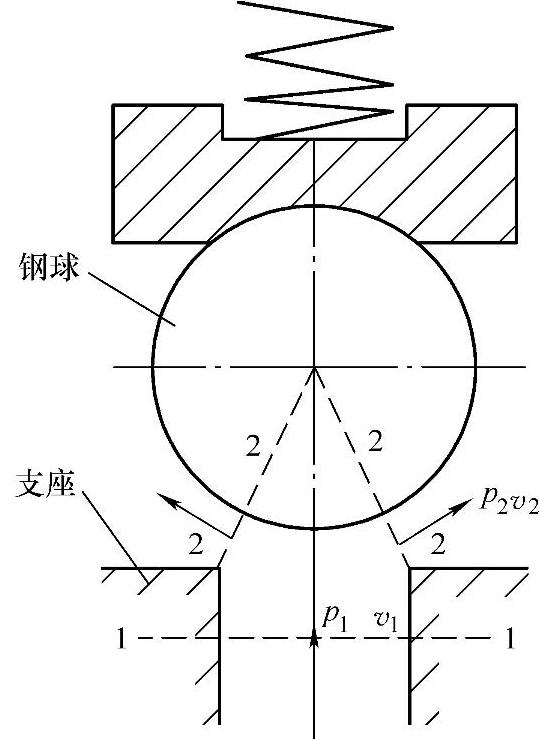
图1-9 安全阀流量计算
如图1-9所示，在安全阀打开状态取两个截面，一个是油的通道截面1-1，一个是在钢球支座的通道上以2-2为素线的截锥表面（素线与此处的流速垂直）。假设1-1和2-2为渐变流，根据伯努利方程式，得
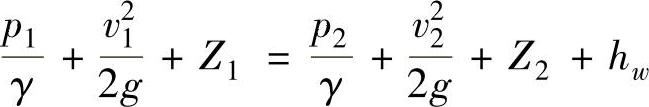
式中 p1、v1——截面1-1上的压力和流速；
p2、v2——截面2-2上的压力和流速。
可以近似地认为截面1-1和截面2-2所在的位置相等，即Z1=Z2。由于截面1-1比截面2-2大得多，故v1比v2要小得多，在计算时可以略去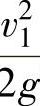
这一项，压力损失这一项放在以后考虑，则得
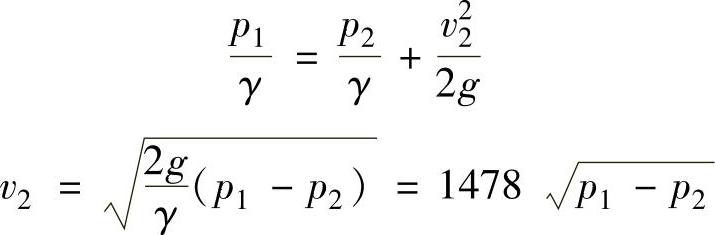
式中 g——重力加速度，g=9.8m/s2；
γ——液压油重度，γ≈9×103N/m3；
v2——2-2截面的平均流速（m/s）；
p1、p2——安全阀前后压力（Pa）。
若以A表示2-2截面面积（m2），则通过2-2截面的流量q（L/min）为
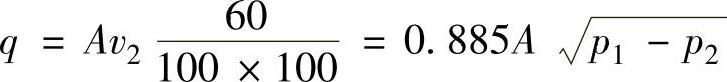
由于局部压力损失及断面收缩，实际流量要比上式求得的小，所以要乘一修正系数c，即
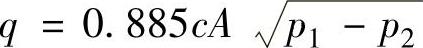
式中 c——流量系数，根据实验，c=0.62～0.75。
4.动量方程
流动液体的动量方程是流体力学的基本方程之一，它是研究液体运动时作用在液体上的外力与其动量的变化之间的关系。在液压传动中，计算液流作用在固体壁面上的力时，应用动量方程去解决就比较方便。
在计算流动液体对接触物体的总作用力时可以用两种方法：一是先求出液体与物体接触的壁面上每点的表面力，即压力和切力，再对整个接触面积分求出总作用力，但此法非常复杂，难以实际应用；另一种是利用动量方程式，在方程式中出现的是被研究的液体段上所作用的外力，以及由这些外力所引起的液体的动量变化，因此仅要求具备液流段边界面上的数据，而不需要液体内部的数据，这就大大简化了计算。下面我们来推导流动液体的动量方程式。
理论力学的动量定律同样适用于液体，即在单位时间内，液体沿某方向动量的增量，等于该液体在同一方向所受外力的和，可表示为
如图1-10所示，有一段液体1-2在管道内做稳定流动，在通流面1-1和2-2的断面处平均流速分别为v1和v2，面积为A1和A2。经过很短的时间Δt后，液体从1-2位置流到1′-2′的位置。因为是稳定流动，故液体段1′-2内各点的流速是不变的，它的体积和质量也是不变的，所以其动量也没有发生变化。这样在时间Δt内，液体段1-2的动量变化将等于2-2′液体段的动量与1-1′液体段的动量之差，即等于在同一时间内经过液流段1-2流出和流入的液体动量的差值，一般用下式表示：
Δ（mv）=（mv2）2-2′-（mv1）1-1′=ρqΔtv2-ρqΔtv1=ρqΔt（v2-v1） （1-2）
式中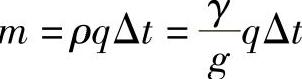
（液体段1-1′或2-2′的质量）；
ρ——液体密度；
q——液体流量。
将式（1-2）代入式（1-1），有
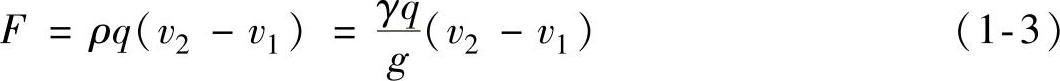
式（1-3）称为液体稳定流动的动量方程式。
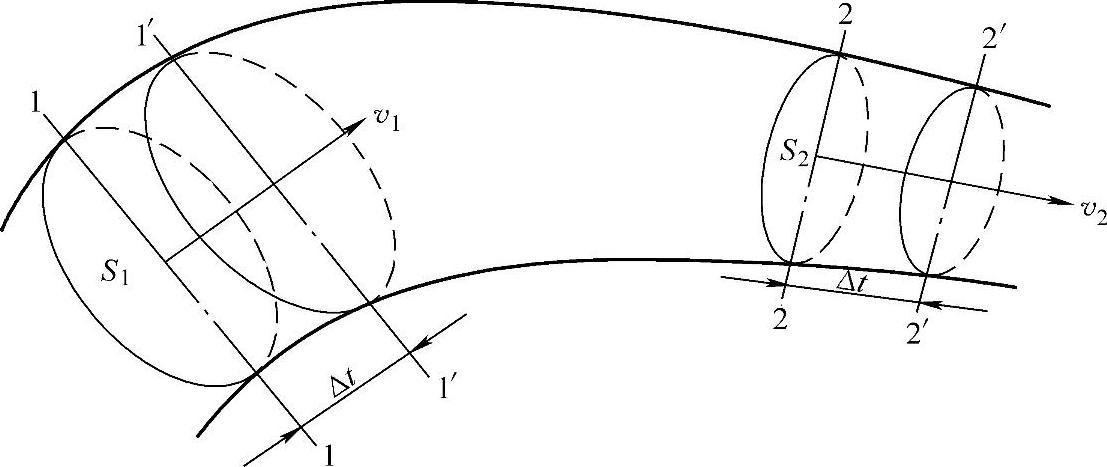
图1-10 流体的动量方程
例：在图1-11a与图1-11b所示的滑阀中，液体流动方向相反，试计算阀芯所受到的液流作用力（取图中阀体与阀芯形成的容积中的液体作为研究对象）。
对于图1-11a，液流初速在轴向的分量为v1=v·cosθ，液流末速在轴向的投影为零，则这部分液体在轴向受到阀芯的作用力为
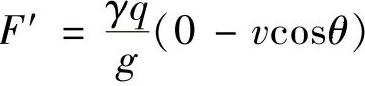
从而液流对阀芯的作用力为
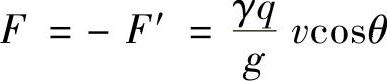
力F的方向与液流的速度v沿阀芯轴向投影方向相同，即向右。
对于图1-11b，液流初速在轴向投影为零，液流末速在轴向的分量为vcosθ，则这部分液体在轴向受到阀芯的作用力为
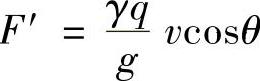
从而液流对阀芯的作用力为
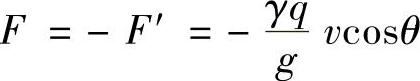
力F的方向与液流的速度v沿阀芯轴向的投影方向相反，即也向右。
本例中，由于液体通过阀口流动而产生的对阀芯的轴向作用力通常叫作液动力。由于在阀口的关闭过程中，流速很高，因而此力往往很大，尤其是对大流量的阀，在高压下工作（此时流速v也很大）时这个力更大，需要我们在设计滑阀时认真对待。
上述计算都只考虑了液流对阀芯的稳态液动力，即认为液体在滑阀中的流动为稳定流动，而实际上液体的流动是非稳定流动，故还要考虑瞬态液动力的作用。这在滑阀设计中要根据具体情况进行计算。
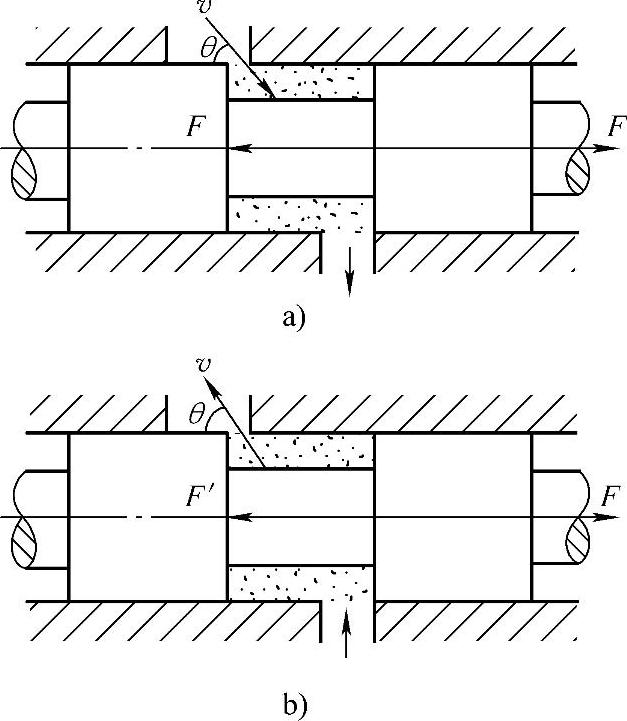
图1-11 液压流经滑阀时的液动力
有关现代冶金设备液压传动与控制的文章
- 详细阅读
-
公域流量与私域流量的重要性详细阅读
公域流量的两个基本特征即垄断性与付费。从公域、他域引流到自己的私域，以及私域本身产生的流量即为私域流量。既然公域流量和私域流量的焦点主要集中在流量的价格与自主权上，那么认清楚它们就不难了。自主权方面，由于公域流量强调控制，因此企业会沦为平台的附庸，流量是互联网商业和营销的基础，身家性命岂可握于他人之手，因此对流量自主控制的追求是企业的本能行为。......
2023-11-22
-
流量经营成功的三大关键详细阅读
做好流量经营要从三个方面努力商业银行要积极开创流量经营的新模式，重点要从客户流、资金流和信息流三个方面努力，进一步明确战略性业务领域和发展突破口，整合客户、平台、渠道、产品等管理要素，深入推进商业银行流量经营转型和盈利模式转变。......
2023-11-30
-
连续性方程在直角坐标系中的应用详细阅读
欧拉连续性方程是欧拉在1755年建立的。按欧拉方法，如图1.12所示，首先选取控制体元——固定在空间上的一个确定的、形状任意的封闭体积，位置保持不变。控制体元可以非常小，如小到前文所述的特征体元；或者有限大，这需要根据研究问题所确定。控制体元的形状不会影响所得到的方程。ρv也称质量速度，它是单位时间内通过单位面积的流体质量。......
2023-06-28
-
计算机网络中的流量和拥塞控制详细阅读
进行拥塞控制需要付出代价。总的来说，流量控制是解决“线”或“局部”问题，而拥塞控制是解决子网中“面”或“全局”问题。这种策略重在解决，在拥塞发生后设法控制和缓解拥塞。......
2023-10-22
-
生态流量测量的测流方式详细阅读
应采用与监测断面特点、水流特性及生态流量泄放措施相适宜的测流方式。通过机组发电泄放生态流量的，根据机组的发电功率、工作水头或实测水头等参数推求下泄流量。通过开启闸门泄放生态流量的，根据堰闸类型、闸门开度与上下游水位监测值、流态类型，结合率定的或经验流量系数推求下泄流量。利用水泵抽水泄放生态流量的，根据抽水的效率、水泵净扬程及功率计算下泄流量。......
2023-06-27
-
水位流量曲线关系优化详细阅读
水位流量关系曲线按其影响因素分为稳定的和不稳定的两类。一次洪水按涨落过程分别定线，水位流量关系曲线表现为绳套形曲线。另外，值得说明的是，利用水位流量关系曲线，由水位查求流量时，经常会遇到高水和低水部分的延长问题。......
2023-06-21
-
如何进行流量测算？详细阅读
图X2.4流量模型示意图由上述分析可知，流速面积法测量流量的工作包括断面测量、流速测量两部分。X2.2.2.1断面测量断面测量是在测流断面上布置若干条测深垂线，施测各垂线的水深，以及各垂线相对于岸边某一固定点的水平距离，即起点距，如图X2.5所示。图X2.5断面测量示意图横断面；平面起点距测量的方法很多。X2.2.2.2流速测量当前，国内外在天然河道流速测量中普遍采用流速仪法。X2.2.2.3流量计算断面流量的计算步骤如下：计算垂线平均流速。......
2023-06-21
相关推荐