通过ADAMS软件提供的图形接口模块，将三维实体造型软件UG中建立的机构三维模型导入到ADAMS软件中的。考虑到所关心的问题和仿真的方便，对操作机构作适当简化后，用ADAMS软件包建模。约束关系的添加要充分考虑实际操作机构中可能存在的约束，遗漏任何一个约束关系都会严重影响到输出结果。3）仿真过程的控制 在ADAMS软件中，为了实现对仿真过程的控制，需要添加传感器来控制仿真过程的自动终止。......
2025-09-29
非晶态有机固体电子输运模型优化
【摘要】：非晶态分子固体的电子输运局限于分子个体中。电荷与感应极化共同作用的结果是产生了极化子。极化子模型具有严重的局限，不能始终为观察到的行为建立正确的模型。事实上，该模型未能反映出迁移率与电场和温度的关系，而非晶态分子固体的实验已表明这种关系的存在。由于电场的存在改变了位点的能量分布并降低了朝向该方向的平均能带隙，因此可以说非晶态有机固体的电荷迁移率与电场的关系十分密切。
非晶态分子固体（OLED器件的核心）的电子输运局限于分子个体中。通常，用一个分子到另一个分子的定域跳跃（跳跃模型）理论来描述电荷的输运。该模型最初用来表示固体（例如非晶硅）内的输运。
上述模型描述了用网络振动维持的分子间隧道效应，该理论最初是为常规半导体提出的。该模型能够描述具有大量结构或化学缺陷的无序共价晶体内载荷子的运动方式。Conwell首先提出了上述模型[CON 79]，随后Miller和Abra-hams用数学形式进行了描述[MIL 60]。从能量为εi的位点（或陷阱）i到另一能量为εj的位点j的跃迁速率（每秒尝试的次数）可表达为
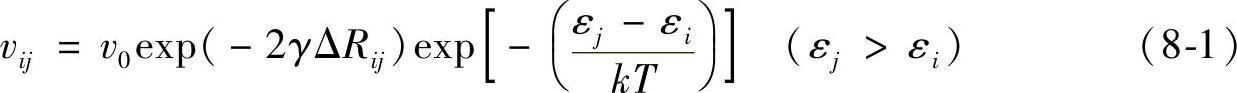
以及
vij=v0exp（-2γΔRij）（εj＜εi） （8-2）
式中，v0为声子振动频率，且被电子向低能态跳跃隧道效应的概率校正（εj＜εi）。此概率取决于位点间距离（ΔRij），γ表示能态i和能态j波函数的重叠。当电子向高能态跳跃时，公式中增加了反映声子吸收概率的波尔兹曼分布（εj>εi）。
如果跳跃理论适用于所有有机半导体，那么与之相反，用于描述这类材料载荷子迁移率的理论取决于材料的性质和结构。极化子理论[GIL 72]通常用于导电聚合物和分子晶体，它们具有窄能带结构。利用无序理论[BAS 81]可得出非晶态有机玻璃的最佳迁移率。
极化子是陷入自诱导电势中的电子或空穴。实际上，电荷在分子位点上停留的时间远长于跳跃时间。电荷和位点相互作用更强，因为电子在位点上停留的时间长于分子中原子核的振动周期（约10-14s）。所以，在电荷位于分子的全部时间内，分子中的原子核的平衡态将发生改变，各平衡态的极化不同。电子首先引起分子的自感应极化，随后将被该极化控制。电子能量将减少，所以将陷入自诱导电势中。电荷与感应极化共同作用的结果是产生了极化子。如果不穿过势垒，极化子就无法移动，移动的方式主要是跳跃。电子处于激发态时的势垒要小于基态时的势垒，因此跳跃过程是由激发态引起的电荷输运。电子激发态的寿命长时，电子的跳跃概率也高。
极化子模型具有严重的局限，不能始终为观察到的行为建立正确的模型。事实上，该模型未能反映出迁移率与电场和温度的关系，而非晶态分子固体的实验已表明这种关系的存在。此时采用B a¨ssler无序理论更为合适。
该理论认为在非完全有序状态下，分子位点的位置和能量可用定域态的随机高斯分布描述。位点能量分布由分子间偶极-偶极起伏引起的永久无序决定，分子又与邻近分子的附加电子相互作用。假设能态的能量和空间分布呈现出高斯型，原因是每个能态都依赖于大量参数，都有着微观的变化。
所以输运是在本征态密度的输运带和禁带（陷阱）中发生的，方向是从输运带朝向禁带，朝向能量更低或更高的位点。如果热激活能不足，向更高能态的跳跃需要电场的支持。
由于电场的存在改变了位点的能量分布并降低了朝向该方向的平均能带隙，因此可以说非晶态有机固体的电荷迁移率与电场的关系十分密切。由于这类材料中的电荷迁移率还与温度有关，非晶态固体的迁移率μ（E，T）可用下面的典型数学表达式给出：
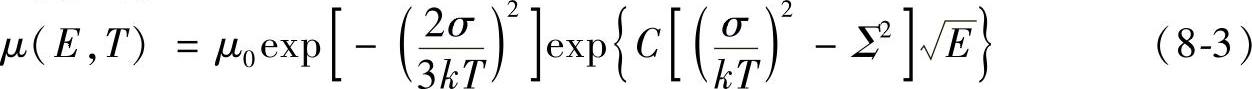(https://www.chuimin.cn)
此经验公式较好地反映了实验观察非晶态有机固体的结果。此式于2025年首次用于拟合聚乙烯咔唑薄膜中迁移率的实验数据。
下面给出了理论基础：
1）能量位点和距离用半高宽度分别为σ和Σ的高斯分布表示。
2）跳跃用前面提到的Millers-Abraham理论描述。
3）电子和声子的耦合相当低，极化子的形成可以忽略。
4）过程是不连贯的，每个跳跃均独立于其他跳跃。
5）材料的陷阱较浅，即接近于能带，所以陷阱具有临界温度Tc，温度低于Tc时输运变得分散。无序模型仅适用于Tc<T<Tg[7]的情况。
6）模型仅在电场强时有效，通常电场应大于105V/cm。这也正是OLED中电场强度的数量级。
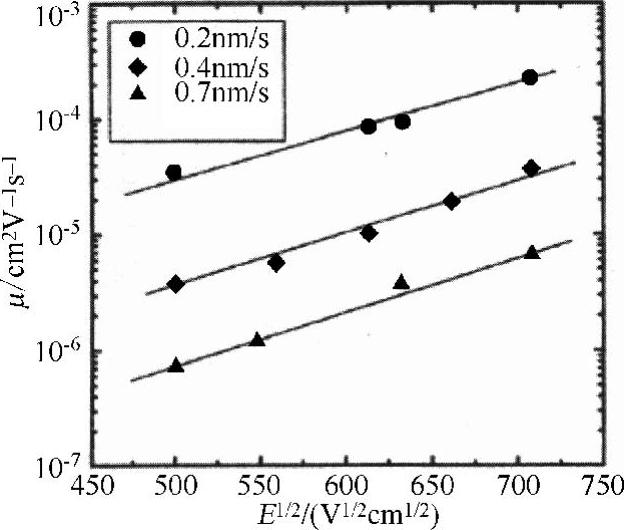
图8-7 测得的各种蒸发率下沉积的AlQ3非晶形层飞行时间电子迁移率
文献[BOR 98]对其他模型做了详细的介绍。然而，无序理论是描述非晶态有机半导体迁移率的最佳方法，尤其是指出了迁移率的对数与电场（SE1/2项）有关以及电场为0时迁移率温度的关系[（2σ/3kT）2项]。如图8-7所示，这种半导体的迁移率典型值介于10-6V/cm2/s和10-3V/cm2/s之间。
相关文章
- 详细阅读
-
非操纵逆转保护装置优化方案详细阅读
非操纵逆转保护装置是防止自动扶梯和倾斜式自动人行道在向上运行时，非人为操纵而改变其运行方向时，起到防止反向运行的安全装置。将自动扶梯或自动人行道钥匙开关转到上行方向，此时抱闸已打开，人为盘动自动扶梯或倾斜式自动人行道的盘车手轮，向下行方向盘动，则非操纵逆转保护装置应该动作。......
2025-09-29
-
精细有机合成实验室的守则优化详细阅读
精细有机合成实验是有机化学实验的重要组成部分。精细有机合成实验所用的药品种类繁多，而且多数药品易燃、易爆、有毒、有害。为了保证实验安全，培养良好的实验习惯，学生进入实验室开展实验时必须遵守实验室规则。严禁在实验室吸烟、饮食、喧哗、打闹。完成实验后认真洗手。若发生安全事故，及时采取相应措施并立即报告实验指导教师。实验结束后，妥善保存实验记录，并根据原始记录及时书写实验报告。......
2025-09-29
-
代表性断路器电弧模型的优化与分析详细阅读
20世纪90年代中期，该问题是低压电器的一个研究热点，这也促进了电弧模型的发展。Lindmayer等人的三维MHD电弧数学模型[15]1998年，Lindmayer基于Flow3D软件，首次建立了较为完整的断路器电弧三维MHD数学模型。近年来，由于发现在低压断路器的灭弧室中布置产气材料，有利于抑制电弧背后击穿现象，提高断路器的限流性能和弧后介质恢复强度，从而提高其开断能力。......
2025-09-29
-
尼迈亚电弧的简单数学模型优化详细阅读
简单的尼迈亚模型是一种经验公式类型的电弧数学模型，按图8-1所示，断路器开断过程可分成4个过程，它们是1）瞬动电磁铁动作过程；2）电弧停滞过程；3）电弧运动过程；4）电弧进入电弧栅片熄灭过程。经过停滞阶段后，电弧开始运动，迅速从动触头转移到导弧板，并在磁场力的作用下向栅片运动，计算这一阶段的电弧电压Uarc需要建立电弧动态数字模型，这里介绍尼迈亚模型，它由L.Niemeyer博士于1984年提出[1]。......
2025-09-29
-
电子元件喷印自由成形技术优化方案详细阅读
目前，喷印自由成形的电子元件主要有：电容器、电感器、电阻器、晶体管和传感器等。图3-43 微型热管网络的喷印成形的过程a）喷印有机墨水 b）逐层喷印墨水 c）在热管网络中渗透低粘度环氧树脂 d）环氧树脂固化，去除易消散墨水美国康奈尔大学在其研制的Fab＠Home Model 1喷印机上，已自由成形电路、有机电化学晶体管、机电继电器、锌空气电池等［1-5，14]。图3-44 Fab＠Home Model 1喷印机......
2025-09-29
-
金属机械器件电子束熔化自由成形技术优化详细阅读
图3-102 EBM自由成形过程原理图典型的电子束烧结自由成形系统通常由电子枪、工作室（真空室）、真空系统、电气控制系统和电源等组成［31，34]。图3-106是EBF自由成形系统中采用的送丝机构。图3-109和图3-110是美国NASA用电子束烧结自由成形的铝件。对于电子束烧结自由成形的尺寸为150mm×150mm×160mm的钢工件而言，其尺寸精度在±0.3mm以内，相当于铸造的精度。表3-5 电子束烧结自由成形的Ti6Al4V与H13模具钢的机械性能比较......
2025-09-29
-
实验模型及方法详解详细阅读
实验采用对称的双断口结构，图6-25所示为实验模型的平面图及相关几何尺寸，单位均为mm。图6-25 气动斥力实验模型的平面图图6-26 气动斥力测试方法的原理图测量方法的原理如图6-26所示。下面的实验均是采用该方法进行的。图6-29 s=2mm，Im=4.2kA时的实验波形及电动斥力、气动斥力随时间的......
2025-09-29
相关推荐