莫兰指数I用标准化统计量Z来检验n个区域是否存在空间自相关关系，当Z值为正且显著时，表明存在正的空间自相关；当Z值为负且显著时，表明存在负的空间自相关，相似的观测值趋于分散分布；当Z值为零时，观测值呈独立随机分布。交通事故发生率的莫兰指数I为0.28，G观测值为0.001126，表明交通事故发生率具有强烈的空间相关性、聚集性，即某地的交通事故与该地区的位置有关。图3.21局部莫兰指数......
2025-09-29
如何测量光通量及其方法介绍
【摘要】：通常我们感兴趣的量是光源向各方向发射的总光通量。图6-4 用光度测定法测量光通量6.1.5.1.2 积分球上述空间积分法十分繁琐，但它们是建立基于发光强度的通量标准所必需的。光通量为Φ的待测灯（光源S）可放置于球体内的任何位置。
通常我们感兴趣的量是光源向各方向发射的总光通量。在某些情况下，我们还对光源向给定立体角（对于点状光源）方向发射的部分光通量感兴趣，所以要忽略向不希望的方向发射的光通量，例如LED的背面。
6.1.5.1 总光通量测量方法（[CIE 89]）
6.1.5.1.1 光度测定法
测量总光通量Φ的基本方法是根据式（6-7）的定义，在空间的4π立体弧度内对发光强度进行积分。I由前述的光度测定法得到（用双轴测角仪测量方位角φ和倾斜角θ）。还提到的一点是该定义假设光源为点状的（所以应在远距离测量）。
如果用式（6-8）的定义可解除上述限制，即在包围光源的任意体积的表面总面积上对照度进行积分。这种测量方法以特殊的方式考察了任意半径R的球体表面（当然最低要求是球体将光源包含在内，而且当入射过于倾斜时，不会危及检测器校正“余弦”的行为）。光源无需放置在球体的中心，即使这是它平常所在的位置。在任何情况下，测量的目的都是确定半径为R的球面上的照度，可利用以下关系式：
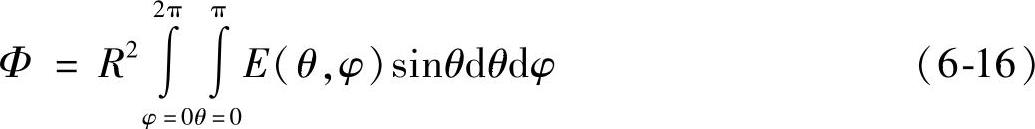
下面的变换在计算中很有用（见图6-4中的单位半径情况）：
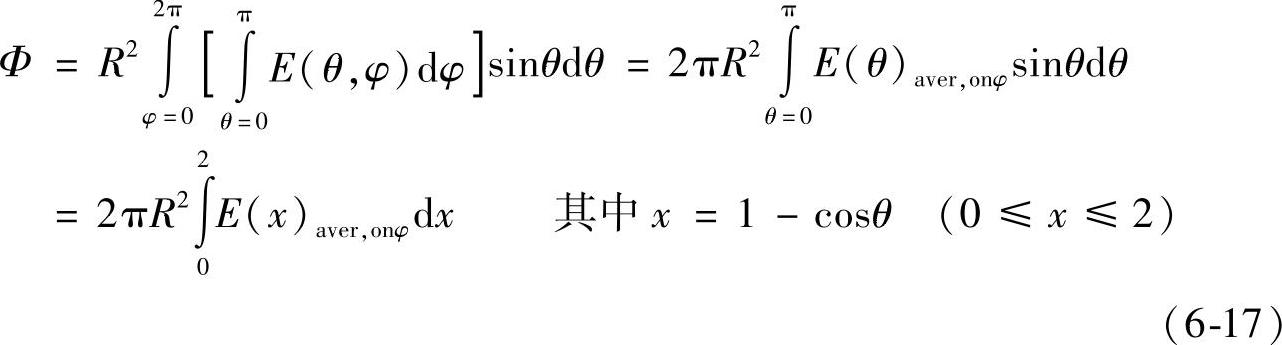
这样，Φ的计算转化为测量笛卡尔图中曲线Eaver.onφ（为x的函数）下方的面积，再将其乘以2πR2。
角度测量间隔必须根据光束分布的尖锐程度进行恰当的选择。
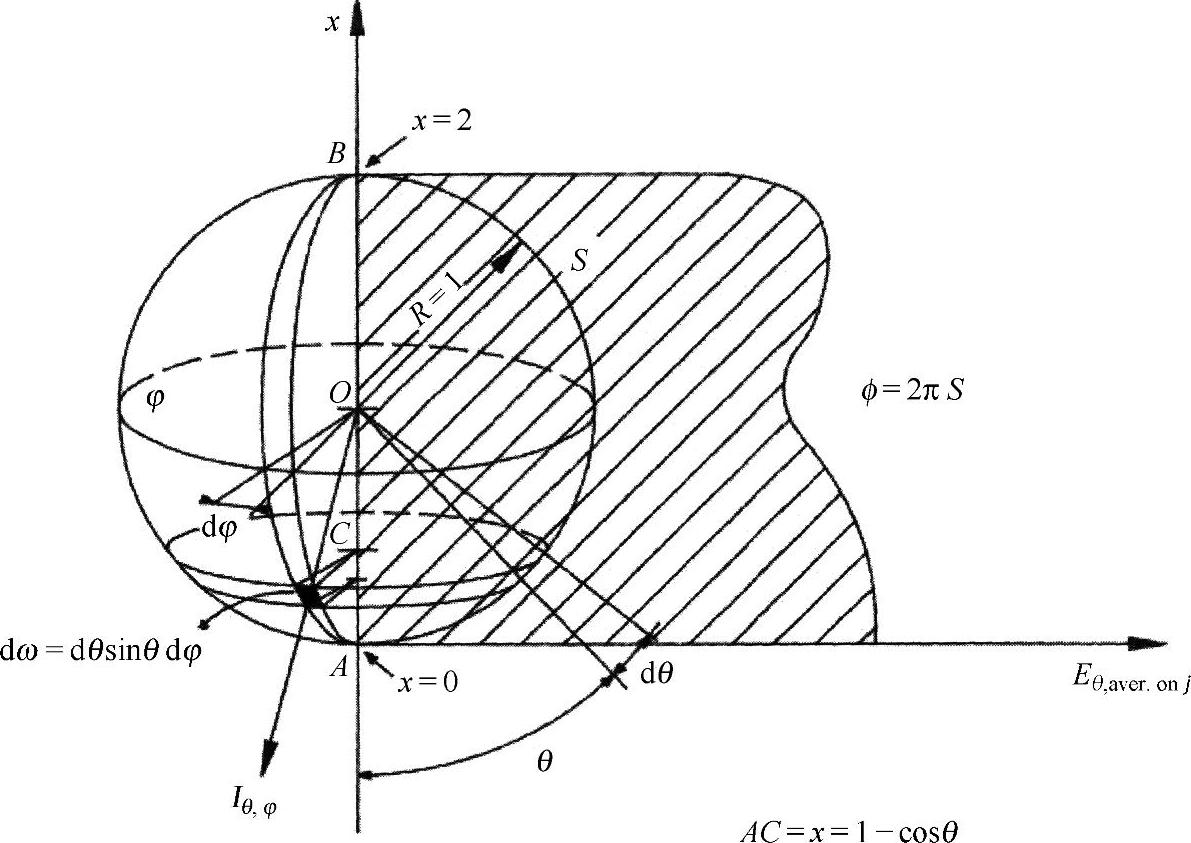
图6-4 用光度测定法测量光通量
6.1.5.1.2 积分（乌布利希）球
上述空间积分法十分繁琐，但它们是建立基于发光强度（或基于标准勒克斯计测得的照度）的通量标准所必需的。相比之下，积分乌布利希球法以光学方式进行积分，目的是直接得出被测光源的总光通量。然而，这是一种比较法，它假定另一个光源有着相同的空间和光谱分布，且光通量已知（标准灯）。球体通常被认为是设备中体积较大的部分，因为它必须包含电灯和任意尺寸的发光体，但对于LED来说，这不是否定这种方法的理由。
设球体的半径为R（见图6-5），内壁覆盖白色的光谱为非选择性的涂层。假设涂层的反射比ρ（即某点反射光通量和入射光通量之比）很高且每一点的反射比大小相同。另外，涂料必须是完全哑光的，即具有理想的漫反射系数，能够均匀地反射各方向的光（此处称为各向同性、均匀或朗伯反射）。光通量为Φ的待测灯（光源S）可放置于球体内的任何位置。
设A为内壁上任意一点，光源的直接照度Ed使该点的照度为E，而球体内壁连续反射使该点照度增加了Er，即间接反射照度。理论上，内壁的间接反射照度与A的位置无关，可表示为
上式的关系十分简单，显然照度Er与光通量Φ成正比。上式的证明从下面的能量平衡关系式开始：
光源发射的光通量Φ=球体（面积为S）吸收的总光通量：
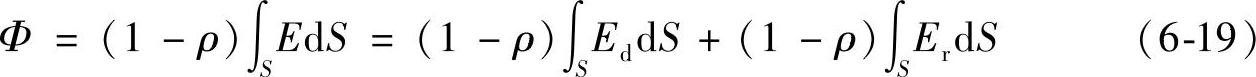
然而，Φ还可根据式（6-7）的一般定义写为
所以平衡关系变为
为了将式（6-21）转化为式（6-18），还需证明内壁每点的Er相等，因此A点的照度ErA与A点位置无关。这一照度为内壁上来自所有A′点（面积dS′）单元亮度的积分。“从观察者的角度看”，每一点对照度的贡献用式（6-2）定义的该点亮度表示（基本立体角为距锥体顶点距离为d处的横向面积与距离二次方之比）。从而证明了下面一系列公式中的第3个关系式：
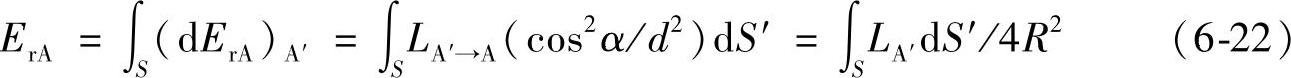
为了得到上面的最后一个关系式，利用内壁各向同性的性质消去L下标中的箭头，因为对于这种内壁，LA′与方向无关。到此为止，证明了ErA与A无关（=Er）。式（6-21）转化为式（6-18），表明内壁上任意一点的反射照度与待求的Φ成正比，与该点和光源的位置无关。此外，还应注意光源的尺寸对以上推理没有影响。所以，采用这种测量方法时，可将勒克斯计的测量头至于内壁的任意一点；另外，插入遮蔽屏使测量头（见图6-5）避免被光源直射。光通量由读数和式（6-18）直接算出。
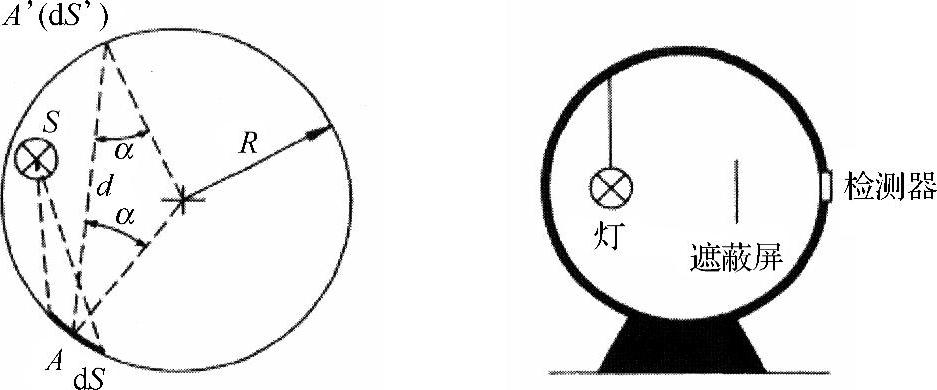
图6-5 积分乌布利希球法
然而，实际情况并不如我们期望的这么理想。遮蔽屏（也涂为白色）、测量单元的开口、灯的支架以及灯本身（最终包括它的发光体）都是内壁上自由反射的障碍，因此必须用小于1的系数k（Bulk Factor，体积因数）对公式进行校正：
不能再用此式计算间接照度，因为体积因数是不可测定的。此外，整个表面的反射比也不是严格处处相等的，而且会随着时间发生变化（因锈蚀、灰尘等原因）。
所以积分球专门用于替换模式。待测灯（光通量为ΦT）和参考灯（光通量为ΦR）被依次引入球体中，分别记录用勒克斯计（不需要校准，因为测量结果仅与照度成正比）测得的内壁上的mT和mR。所以光通量之比与读数之比成正比：
(https://www.chuimin.cn)
实际中，只是偶尔使用参考灯测量法，用来确定球体系数（Sphere Factor，SF）：
SF=ΦR/mR （6-25）
这时，被测的光通量可仅由下式求得：
ΦT=SF×mT （6-26）
上式假设当辐射依次来自被测灯和标准灯时，以下两个参数具有一致性：
1）涂层的反射率ρ相同。当两盏灯的光谱不一致性很高时，这一点难以满足，因为涂层的光谱非选择性的假设没有得到严格满足；
2）体积因数相同。有一种方法可使我们不受此限制。
下文对以上两个问题作出更进一步的分析。
对勒克斯计还有以下要求：测量单元必须进行余弦校正，因为它接收面对测量头的整个半球的光通量；此外，当使用多色测光法时，显然测量单元的光谱必须与V（λ）相同。
1.关于内壁反射
式（6-23）表明，为了增加测量敏感度，应使用尽可能白的涂料（ρ接近1）。例如，如果将ρ从0.80提高至0.98（基于氧化镁涂料的典型值），敏感度（乘以系数Φ）将增加12倍。但是问题还是存在，因为反射率ρ大时，ρ的变化（随时间或随λ变化）对球体系数的影响也大。因此，若ρ=0.80，ρ减小1%将使球体系数减小5%；而ρ=0.98时，球体系数将减小50%！出于同样的原因，ρ的光谱恒定性更为关键，因为被测灯的光谱与校准用的参考灯不同。如果光谱反射系数ρ（λ）随λ的变化而变化，那么任何材料的全局反射系数ρ将与光源的光谱有关。
球面理论依赖于内壁涂层各向同性漫射的假设。只有在这种情况下，内壁上连续的反射将使每一点的（间接）照度均匀。这一假设仍然不是完美的，由于光源辐射是方向性的（对于LED来说是常见情况），均匀性是不那么容易实现的。当涂料的反射率低时，以上现象尤为突出。
2.大型光源的测量
式（6-24）假设参考灯面前和未知灯面前的体积因数k相同。该假设没有考虑两个光源体积不同的情况。为了克服这个困难，使用辅助灯的一般方法是合适的[CIE 89]。将辅助灯放进球体内，用附加的遮蔽屏将其与面前的测量窗、参考主光源或未知主光源隔开。球体理论表明连续的反射使内壁的（间接）照度趋于均匀。此时这样的描述较为贴切：在球体内物体占用一定空间的情况下，连续的反射将被阻碍，与光源的初始位置无关。换句话说，当球体被辅助灯或主灯照射时，如果这两盏灯在测量时同时存在，体积因数实际上是相同的。由此产生了下面的方法：
1）用被测灯作为主灯，交替打开未知灯（T）和辅助灯（A），记录测量值mT和mA。用式（6-24）中的下标R替换下标A，该式仍然成立，因为两种测量方法的体积因数kT相同。
2）用参考灯作为主灯，进行同样的操作，测量mR和mA′。用下标A′替换式（6-24）中的下标T后，该式也仍然成立，因为两种方法的新体积因数kR相同。将两种情况结合，最终得
这时需测量4个照度值才能求得光通量。上式表明比值mA′/mA只不过是两种结构下体积因数的比值，对应用直接法获得的结果起到校正系数的作用。只有该比值不等于1时才必须使用辅助灯法，实际中这种情况经常出现。应注意，ΦA是无需已知的，因为它不出现于式（6-27）中，仅需保证它在整个测量过程中是稳定的。
3.LED在球体中的位置
即使理论上光源可位于球体内的任何位置，但为了减小参考灯和未知灯间的不一致误差，建议将LED放置在球体的中心附近（见图6-6a）。遮蔽屏大致位于光源和检测器的中间。后来提到的辅助灯应靠近检测器对面的内壁，它的遮蔽屏置于附近。当测量方向性很强的LED（不向后面发光）时，还可将其放置在内壁附近，减轻了操作上的困难（见图6-6b）。
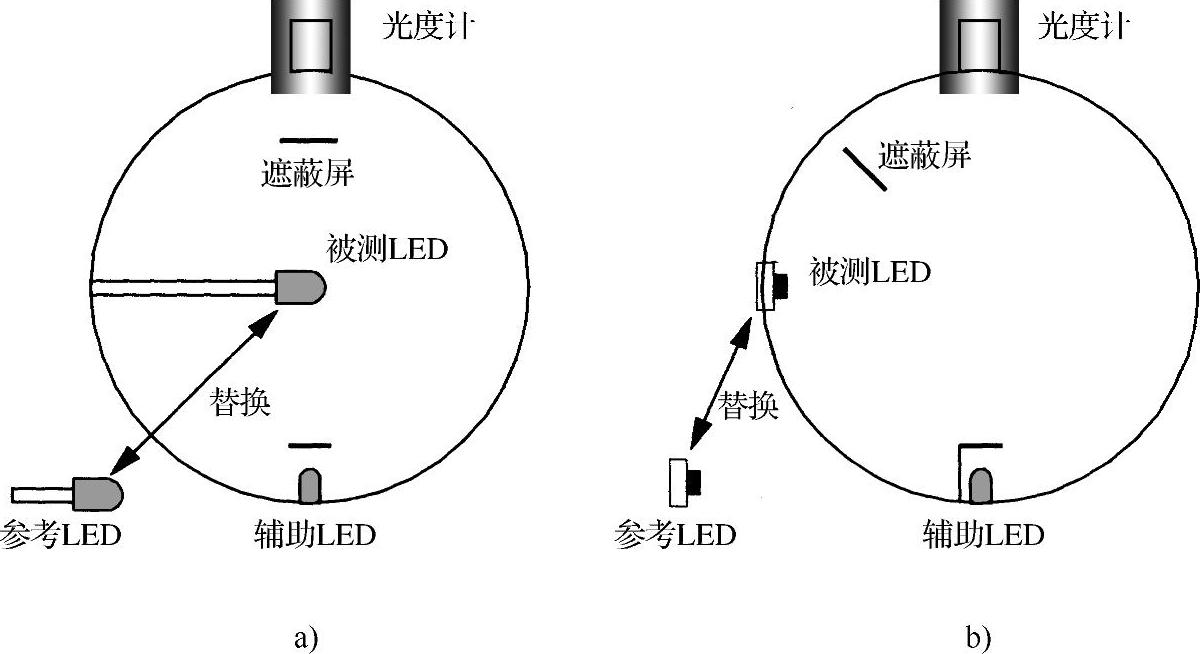
图6-6 测量球体内LED总光通量时建议的空间布置
a）适用于所有LED b）适用于无后向发射的LED
用于LED测量的球体，其直径一般在20～50cm之间。大的直径可以提高内壁照度的空间均匀性（因为遮蔽屏的体效应更低）和测量精度，但会降低测量敏感度（按直径的二次方下降）。值得注意的是，如果比较相同几何结构（体积相同、辐射图相同）的光源，空间不必是球形的，例如采用平行六面体盒子就足够了。
4.光谱辐射计的使用
光谱辐射计可以代替勒克斯计作为内壁检测器，如果光谱辐射计用6.1.6.4节所述的方法测量能通量的光谱密度，那么可根据测量结果推导出LED的光通量。这种方法可克服上文提到的与涂料的可选性质和测量单元不匹配有关的测量困难。
6.1.5.2 测量“部分光通量”
测量特定立体角处电灯的部分光通量时，假定检测器放置的位置足够远，从而认为光源是点状的。由于空间的原因，这并非总是可行的。测量LED时，要从实用主义的角度出发，并且注意实验过程的统一性，这在发光强度测量中已经做了强调。CIE推荐使用“部分光通量”的概念，要求测量窗为直径50mm的圆形开口。“部分光通量”的定义为：指定角度开口锥体内传导的光通量，锥体与LED机械轴成一条直线，锥体的顶点位于LED的前端。当平面开口角为x度时，锥体顶点至位于锥体轴的测量窗中心点间的距离d（mm）必须按下式设置：
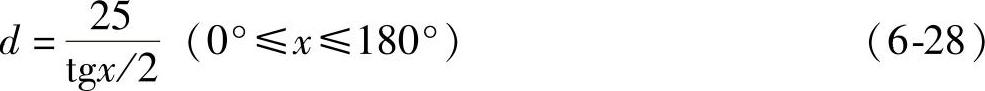
“部分光通量”的符号为ΦLED，x，其中x为锥体的角度开口，单位为度。根据前文的解释，这一光通量具有任意性，其优点是简单，可用于测量任何类型的LED。
建议使用与定义相符的测量结构，如图6-7所示。遮蔽屏放置在开口和测量单元中间，在完全遮挡住测量单元所视开口的基础上，遮蔽屏的尺寸应尽可能小。LED和球体开口间的距离不能太远，以避免寄生环境光线对测量的影响。
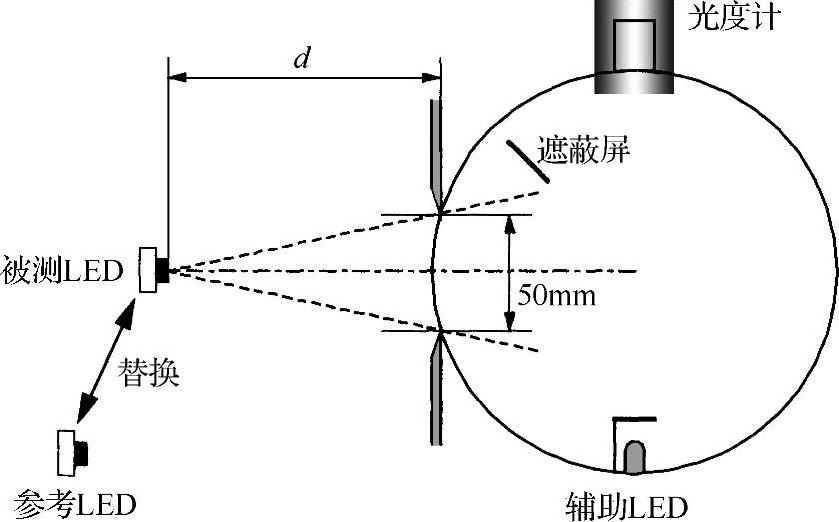
图6-7 CIE推荐测量LED部分光通量的结构
相关文章
- 详细阅读
-
氨基保护方法及常用试剂介绍详细阅读
氨基存在于许多生物活性分子中，如氨基酸、多肽、糖肽、生物碱等，氨基的保护在有机合成中占有重要地位。叔丁氧羰基保护的氨基化合物能够经受催化氢化、强烈的碱性和亲核反应条件。叔丁氧羰基保护氨基在碱性条件下进行，反应条件温和。在DMAP存在条件下，Boc2O甚至可以实现对酰胺—NH及吲哚—NH的保护。常用的保护试剂为Fmoc-Cl或Fmoc-Osu，在 NaHCO3或Na2CO3存在下，一般均能获得较好的收率。......
2025-09-29
-
测量工具和方法：如何选择最合适？详细阅读
测量工具是指能够单独地或者连同辅助设备一起进行测量的器具。绝对测量时测得的数值是被测量的绝对数值。综合测量是指同时测量工件上的几个参数，综合判断工件是否合格的测量方法。在线测量是指在零件的加工过程中对工件进行测量。测量的目的仅限于发现和挑出废品。......
2025-09-29
-
功率类型及相关测量方法详细阅读
在直流电路中，直流电源提供的功率全部为有功功率。有功功率与视在功率的比值称为功率因数，用cosφ表示，cosφ=P/S。为了减少电动机的无功功率，应选用合适的功率，避免出现“大牛拉小车”或让电动机空载运行的情况。图2-12 用电压表和电流表测量功率的两种测量电路......
2025-09-29
-
电流测量电路优化方法详细阅读
电流测量有两种方法：直接测量法和间接测量法。低电压、小电流电路适合用直接测量法测量电流，高电压、大电流电路适合用间接测量法测量电流。测量直流电流要选择直流电流表，测量交流电流则要选择交流电流表。图2-4 利用电流互感器间接测量一相交流电流的电路使用钳形电流表也可以测量电路中的交流电流值。......
2025-09-29
-
外径千分尺测量方法优化详细阅读
外径千分尺常简称为千分尺，它是比游标卡尺更精密的长度测量仪器，常见的外径千分尺如图3-14所示。图3-14外径千分尺1—尺架；2—固定测砧；3—测微螺杆；4—螺纹轴套；5—固定刻度套筒；6—微分筒；7—调节螺母；8—接头；9—垫片；10—测量力恒定装置；11—锁紧螺钉；12—绝热板外径千分尺的读数方法如下。使用外径千分尺时的注意事项如下。根据被测工件的尺寸，选择普通游标卡尺和量程为0～25 mm的外径千分尺进行测量。......
2025-09-29
-
初速测量技术的精准应用方法详细阅读
目前, 利用旋转弹丸的章动测弹丸自转速度国内已经做出, 试验结果在章动角≥1.2°时能正常检测出自转速度。利用地磁传感器检测弹丸旋转圈数也已由试验证实原理可行。由式 可得Rb = 1 - cosα = 0.007 454 = 0.745 4% , 可见在使用的空间角等概率的情况下, 进入盲区射击的机会是很小的。......
2025-09-29
- 详细阅读
相关推荐