扶手带的主要性能指标是抗拉强度和抗疲劳性能。可以在试验机上设定对扶手带的各种弯曲度、试验的速度以及张紧力。......
2025-09-29
光度计/辐射计应具备的性能
【摘要】：6.1.3.2 角响应和空间响应光度计或辐射计必须考虑“余弦定律”[见式（6-6）]，即它们对确定的平行入射光的响应必须与入射光和接收平面法线间入射角的余弦值有关系。
由于我们对光度值和辐射度值感兴趣，所以基本仪器应为光度计或辐射计，它们的作用分别是测量照度（单位为lx—所以也叫勒克斯计）和辐照度（单位为W/m2）。这些仪器由测量头和电子电路组成，前者包括检测器、滤波器和入口，后者的作用是放大和测量检测器输出端的电子信号。
6.1.3.1 检测器
最常用的检测器是硅光敏二极管，其短路电流是有用的输出信号，称为光电流。它的光谱灵敏度覆盖了带宽从近紫外光至近红外光的范围，穿过整个可见光区，峰值约为900nm，在约1100nm处急剧降低。它还表现出良好的幅值线性度（进入的光通量高于几十的情况下，光电流与光通量成正比）和可见光区内良好的热稳定性。
6.1.3.2 角响应和空间响应
光度计或辐射计必须考虑“余弦定律”[见式（6-6）]，即它们对确定的平行入射光的响应必须与入射光和接收平面法线间入射角的余弦值有关系。当入射光覆盖的角视场较大时，上述要求尤为重要，比如积分球测量方法（见6.1.5.1.2节）。据此，制造商提出了“余弦校正器”，可连接在仪器上，也可取下。在测量发光强度时，该问题则不是特别关键，因为入射光覆盖的角视场很窄，近乎于垂直。
测量“LED的平均发光强度”（见下文）时，我们工作于近场区域，检测器的有效表面仍必须具有良好的空间均匀性，使全部进入开口的辐射以相同的权重进行测量。
6.1.3.3 光谱响应
设s（λ）为检测器（包括滤波器）的光谱灵敏度，即波长为λ时，输出电信号Y（根据不同情况，为电流或电压）与用能量单位表示的输入亮度Xe（一般为辐射功率，即光通量或其空间密度）之比：s（λ）=dY（λ）/dXe（λ）。如果入射辐射的光谱分布为Xeλ=dXe/dλ，则输出电信号Y可表示为
当使用辐射计时，（Y表示辐射度），s（λ）在入射辐射的光谱波段必须尽可能保持恒定。
相反，光度计的s（λ）与其最大值[s（λ）rel]的相对值必须尽可能地接近V（λ），这种情况称为“光谱匹配”。失配时的差异取决于被试光源和仪器校准光源间的光谱偏差。如果两个光源的光谱相同，则偏差为零。文献[CIE 82]和[CIE 87b]对此进行了研究。描述检测器特性的其他推荐方法在文献[CIE84a]中给出。
6.1.3.3.1 基于4积分法的失配校正
考虑检测器失配后，应引入校正因数实现严格的照度测量。有以下多个要求：检测器的光谱敏感性、两个被试光源和校正仪器用的电灯的光谱含量。
用光谱敏感性为s（λ）的勒克斯计，并给定被试光源照度ET的量度mT和参考照度ER（标准）的量度mR，假设已知T和R的能谱密度，可得出下面的关系式：
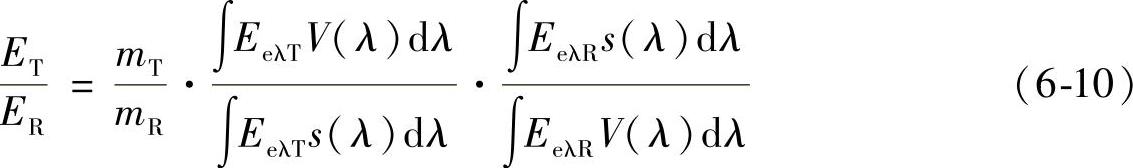
上式4个积分项将ET和ER的光谱密度与s（λ）和V（λ）结合起来，该项被称为搜索光谱密度（下文用F表示），如果F=1，照度的比值等于测量值的比值。此方程式来源于下列关系式：
基本光度定律：
E=KM∫EeλV（λ）dλ （6-11）
勒克斯计的传递函数：
m=∫Eeλs（λ）dλ （6-12）
两式均适用于T和R。(https://www.chuimin.cn)
在校正因数中，所有光谱密度和光谱敏感度都可用绝对值或相对值表示，因为它们同时出现在分子和分母中。
参考条件下的校正可得到勒克斯计的常数c：
c=ER/mR （6-13）
于是有
ET=cmTF （6-14）
每个被测试的光谱分布都有特定的校正因数F。只有当匹配完美[s（λ）与V（λ）成正比]或被试灯和参考灯的相对光谱相同时，F才等于1。应用于LED时，根据上一句话可得出这样一种方法：收集一系列以主颜色为中心的标准LED，实现被试LED与具有相同光谱的参考LED间的直接比较；另外这种方法还无需确定校正因数。目前，这种参考LED仍较少见而且昂贵，但可以预见，它们将越来越常见。
基于4积分法的校正显得冗长而乏味，需确定多个光谱，从而促使人们寻求一种利用式（6-1）的直接确定待求光度值的方法，式（6-1）将光度值和与之对应的光谱能量密度联系起来，光谱能量密度可由6.1.6节的某一种光谱辐射度测量法（Spectro-radiometry）确定。
6.1.3.3.2 勒克斯计的f1′值[CIE 87b]
光度计的光谱失配可用f1′值进行综合定性。该指数用一种特殊的方式表达了测量随后指定的光源的偏差，与测量人员是否使用被考察的光度计还是完美匹配的光度计有关。指定的光源为CIE的光源A（色温为2856K的钨丝灯——电灯的色温为相同相对光谱黑体的温度），它经常用于光度计的校准。该指数将光源A的光谱分布Sλ，A的s（λ）rel和V（λ）联系了起来，它的定义为
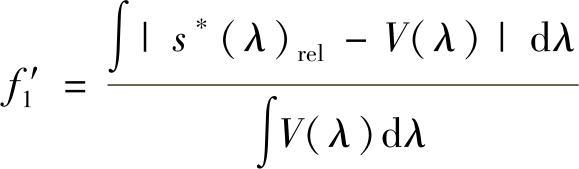
式中
经观察发现，f1′值始终是为正，仅在完美匹配时为0。由于它的定义不反应被测辐射的光谱分布，所以它不是待施加误差项或校正项。然而，f1′值可代表测量“白色”光源时的误差限，前提是光度计已用光源A进行了校准。当测量白光LED时，建议仪器的f1′值不超过3%。
6.1.3.3.3 彩色LED的测量
测量单色LED（带宽窄）时，即使f1′值较低，检测器失配造成的误差也会很高，因为此时在大光谱范围内，误差补偿不再发挥作用。这种情况在测量红光或蓝光LED时尤为严重，因为它们的光谱位于V（λ）曲线右翼和左翼，远离最大值（见图6-2的V（λ）曲线和s（λ）rel曲线，根据检测器制造商的意愿，它们在相
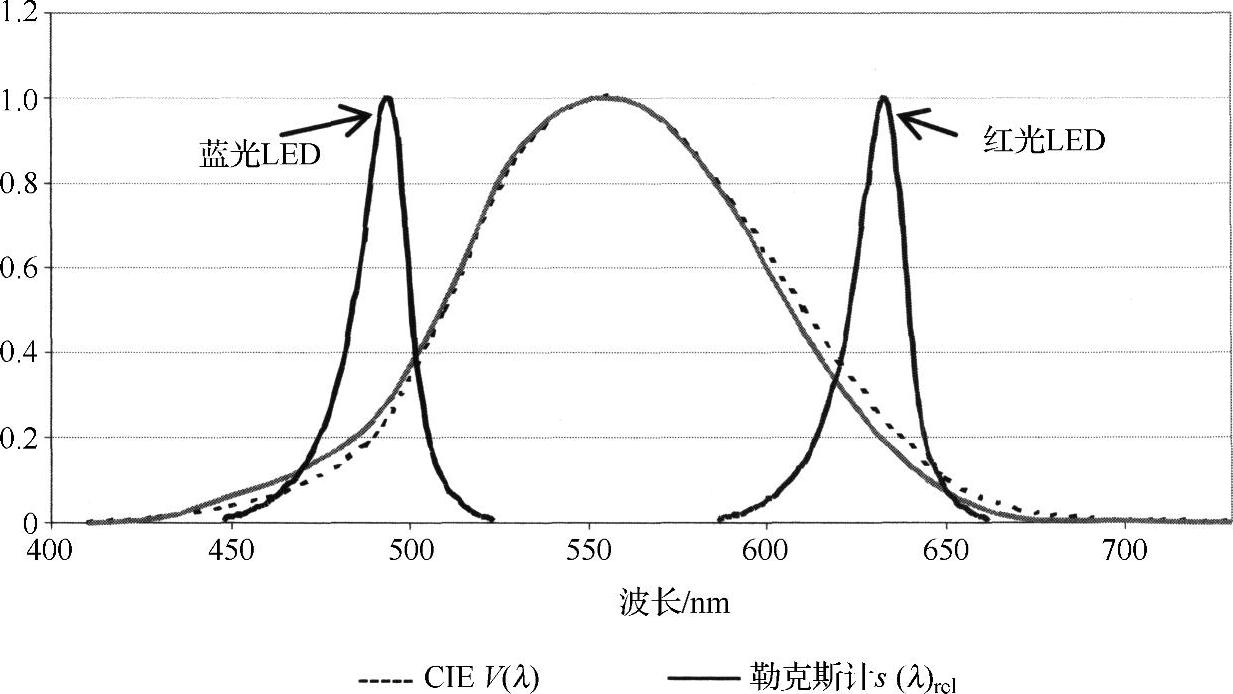
图6-2 蓝光LED和红光LED的光谱以及V（λ）和s（λ）rel曲线
近波长处出现最大值，且在曲线中心附近近乎重合，但在两翼处未必重合）。
对于上述的精确校正，为了避免冗长而乏味的计算，正如已经提到的，我们更喜欢直接应用式（6-1）处理用光谱辐射度测量法获得的数据。
相关文章
- 详细阅读
-
工业铜及合金的牌号与性能表详细阅读
工业纯铜共分为四个组别，即纯铜、无氧铜、磷脱氧铜和银铜等，工业纯铜的化学成分及力学性能见表5-1。铸造黄铜主要有硅黄铜、锰黄铜、铅黄铜等。表5-2 常用黄铜的化学成分及力学性能3.青铜代号常用的青铜主要分为加工青铜和铸造青铜。白铜的牌号以字母“B”为首，其后的数字为平均含Ni量，而Cu为余量。......
2025-09-29
- 详细阅读
- 详细阅读
-
MCCB仿真分析：探究电路保护器的性能详细阅读
由以上仿真结果和实验结果对比可以看出，用MHD仿真MCCB的模型中，动触头的运动过程对电弧电压以及电弧能量的准确性影响非常重要，同时，通过实验验证了在仿真中采用ANSYS Emag软件计算电磁场，用FLUENT计算流场的耦合方法的有效性和准确性，因此在低压断路器的仿真中，为了得到更为准确的计算结果，动触头的运动过程必须在仿真模型中予以考虑。......
2025-09-29
-
地铁紧急疏散：自动扶梯的专用性能要求详细阅读
因此有必要对最大制动距离提出要求。由于地下建筑空间有限，多数地铁站的固定楼梯不足以紧急疏散乘客，需要借用自动扶梯作为紧急通道。GB 16899—2011在“术语和定义”中以注的方式指出：“自动扶梯是机器，即使在非运行状态下，也不能当作固定楼梯使用。”地铁多是地下建筑，自动扶梯的井道存在地下渗水和地下腐蚀性气体，因此要求自动扶梯的机件必须有很好的耐水、耐腐蚀能力。......
2025-09-29
-
钛及钛合金的焊接性能分析与优化建议详细阅读
由于钛及钛合金的热容量大，使热影响区金属在高温停留的时间较长，焊缝晶粒因此变得粗大，容易引起焊接接头产生过热倾向，使焊接接头塑性明显降低。尤其是β型钛合金，焊接接头塑性下降最为明显。由于合金元素含量较高，焊接性较差，是一种高强度、高淬透性合金，厚度为12mm的TC10合金焊接时，会出现热影响区裂纹，而在焊前预热250℃时，可预防裂纹并能提高接头塑性。4）正常氢含量的钛及钛合金焊接时，不会出现氢化钛。......
2025-09-29
-
镍及镍合金的成分和性能详解详细阅读
镍基耐蚀合金具有独特的物理、力学和耐腐蚀性能，镍基合金在200～1090℃的范围内能耐各种腐蚀介质的腐蚀，具有良好的高温和低温力学性能。常用镍及镍合金的耐腐蚀性见表7-3。表7-1 常用镍及镍合金的物理性能和力学性能表7-2 常用镍及镍合金的化学成分表7-3 常用镍及镍合金的耐腐蚀性注：表中A—可接受；G.E—良好至优秀；NR—不推荐使用；X—试验。......
2025-09-29
相关推荐