实例分析：包容、检验、合格条件和几何公差

1.包容要求

1）包容要求的公差解释

包容要求是相关公差原则中的三种要求之一，适用包容要求的被测实际要素（单一要素）的实体（体外作用尺寸）应遵守最大实体边界，被测实际要素的局部实际尺寸受最小实体尺寸所限；形状公差t与尺寸公差Th（Ts）有关，在最大实体状态下给定的形状公差值为零；当被测实际要素偏离最大实体状态时，形状公差获得补偿，补偿量来自尺寸公差（被测实际要素偏离最大实体状态的量，相当于尺寸公差富余的量，可作补偿量），补偿量的一般计算公式为t2=|MMS-Da（da）|；当被测实际要素为最小实体状态时，形状公差获得补偿量最多，即t2max=Th（Ts），这种情况下允许形状公差的最大值为

形状公差t与尺寸公差Th（Ts）的关系可以用动态公差图表示，如图4-33（b）所示。由于给定形状公差值t1为零，故动态公差图的图形一般为直角三角形。

2）包容要求的标注标记、应用与合格性判定

包容要求主要用于需要保证配合性质的孔、轴单一要素的中心轴线的直线度。包容要求在零件图样上的标注标记是在尺寸公差带代号后面加写，如图4-33（a）所示。符合包容要求的被测实体（Dfe、dfe）不得超越最大实体边界MMB；被测要素的局部实际尺寸（Da、da）不得超越最小实体尺寸LMS。生产中采用光滑极限量规（一种成对的，按极限尺寸判定孔、轴合格性的定值量具，见项目6光滑极限量规）检验符合包容要求的被测实际要素，通规检验体外作用尺寸（Dfe、dfe）是否超越最大实体边界，即通规测头模拟最大实体边界MMB，通规测头通过为合格；止规检验局部实际尺寸（Da、da）是否超越最小实体尺寸，即止规测头给出最小实体尺寸，止规测头止住（不通过）为合格。

图4-33　包容要求的标注标记与动态公差图

（a）包容要求的标注标记；（b）动态公差图

符合包容要求的被测实际要素的合格条件为

对于孔（内表面）：Dfe≥DM=Dmin，　Da≤DL=Dmax

对于轴（外表面）：dfe≤dM=dmax，　da≥dL=dmin

综上所述，在使用包容要求的情况下，图样上所标注的尺寸公差具有双重职能：①控制尺寸误差；②控制形状误差。

3）包容要求的实例分析

【例4-1】　对图4-33（a）做出解释。

解：①T、t标注解释。被测轴的尺寸公差Ts=0.021mm，dM=dmax=φ20mm，dL=dmin=φ19.979mm；在最大实体状态（φ20mm）下给定形状公差（轴线的直线度）t=0，当被测要素尺寸偏离最大实体状态的尺寸时，形状公差获得补偿，当被测要素尺寸为最小实体状态的尺寸φ19.979mm时，形状公差（直线度）获得补偿最多，此时形状公差（轴线的直线度）的最大值可以等于尺寸公差Ts，即tmax=0.021mm。

②动态公差图。T、t的动态公差图如图4-33（b）所示，图形形状为直角三角形。

③遵守边界。遵守最大实体边界MMB，其边界尺寸为dM=φ20mm。

④检验与合格条件。对于大批量生产，可采用光滑极限量规检验（用孔型的通规测头——模拟被测轴的最大实体边界）。其合格条件为

2.最大实体要求

1）最大实体要求的公差解释

最大实体要求也是相关公差原则中的三种要求之一，适用最大实体要求的被测实际要素（多为关联要素）的实体（体外作用尺寸）应遵守最大实体实效边界；被测实际要素的局部实际尺寸同时受最大实体尺寸和最小实体尺寸所限；几何公差t与尺寸公差Th（或Ts）有关，在最大实体状态下给定几何公差（多为位置公差）值t1不为零（一定大于零，当为零时，是一种特殊情况——最大实体要求的零几何公差）；当被测实际要素偏离最大实体状态时，几何公差获得补偿，补偿量来自尺寸公差（即被测实际要素偏离最大实体尺寸的量，相当于尺寸公差富余的量，可作为补偿量），补偿量的一般计算公式为

当被测实际要素为最小实体状态时，几何公差获得补偿量最多，即t2max=Th（Ts），这种情况下允许几何公差的最大值为

几何公差t与尺寸公差Th（Ts）的关系可以用动态公差图表示，如图4-34（a）所示。由于给定几何公差值t1不为零，故动态公差图的图形一般为直角梯形。

2）最大实体要求的应用与检测

最大实体要求主要用于需保证装配成功率的螺栓或螺钉连接处（即法兰盘上的连接用孔组或轴承端盖上的连接用孔组）的中心要素，一般是孔组轴线的位置度，还有槽类的对称度和同轴度。最大实体要求在零件图样上的标注标记是在几何公差框格内的几何公差给定值t1后面加写，如图4-34（b）所示。

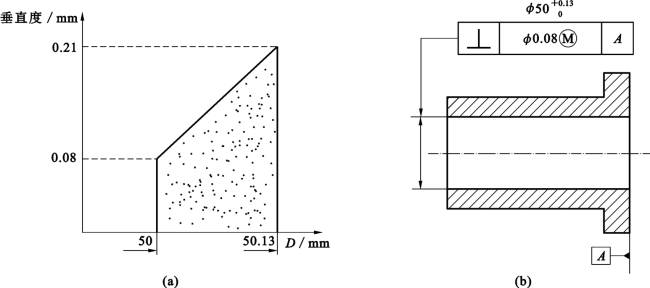
图4-34　最大实体要求

（a）动态公差图；（b）标注标记

当基准（中心要素如轴线）也适用最大实体要求时，则在几何公差框格内的基准字母后面也加写，如图4-35（a）所示。符合最大实体要求的被测实体（Dfe、dfe）不得超越最大实体实效边界MMVB；被测要素的局部实际尺寸（Da、da）不得超越最大实体尺寸MMS和最小实体尺寸LMS。生产中采用位置量规（只有通规，专为按最大实体实效尺寸判定孔、轴作用尺寸合格性而设计制造的定值量具，可以参考几何误差检验的相关标准和有关书籍）检验使用最大实体要求的被测实际要素的实体，位置量规（通规）检验体外作用尺寸（Dfe、dfe）是否超越最大实体实效边界，即位置量规测头模拟最大实体实效边界MMVB，位置量规测头通过为合格；被测实际要素的局部实际尺寸（Da、da）采用通用量具按两点法测量，以判定是否超越最大实体尺寸和最小实体尺寸，局部实际尺寸落入极限尺寸内为合格。符合最大实体要求的被测实际要素的合格条件如下。

对于孔（内表面）：

对于轴（外表面）：

图4-35　基准（中心要素）适用最大实体要求

（a）基准自身形状公差按未注要求；（b）基准自身形状公差采用包容要求

3）最大实体要求的零几何公差

这是最大实体要求的特殊情况，在零件图样上的标注标记是在位置公差框格的第二格内，即位置公差值的格内写0（φ0），如图4-36（a）所示。此种情况下，被测实际要素的最大实体实效边界就变成了最大实体边界。对于位置公差而言，最大实体要求的零几何公差比起最大实体要求，显然更严格。由于零几何公差的缘故，动态公差图的形状由直角梯形（最大实体要求）转为直角三角形（相当于裁掉直角梯形中的矩形），如图4-36（b）所示。

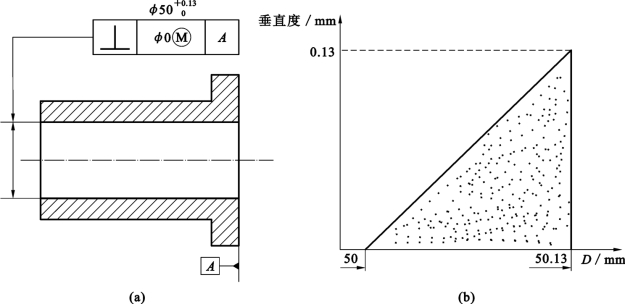
图4-36　最大实体要求的零几何公差

（a）标注标记；（b）动态公差图

另外，需要限制几何公差的最大值时，可以采用如图4-37（a）所示的双格几何公差值的标注方法，一般将几何公差最大值写在双格的下格内。注意：在几何公差最大值的后面，不再加写。此时，由于几何公差最大值的缘故，动态公差图的形状由直角梯形（最大实体要求）转为具有三个直角的五边形（相当于裁掉直角梯形中的部分三角形），如图4-37（b）所示。

4）可逆要求用于最大实体要求

图4-37　几何公差值受限的最大实体要求

（a）标注标记；（b）动态公差图

在不影响零件功能的前提下，位置公差可以反过来补给尺寸公差，即位置公差有富余的情况下，允许尺寸误差超过给定的尺寸公差，显然在一定程度上能够降低工件的废品率。在零件图样上，可逆要求用于最大实体要求的标注标记是在位置公差框格的第二格内，位置公差值后面加写，如图4-34（a）所示。此时，尺寸公差有双重职能：①控制尺寸误差；②协助控制几何误差。而位置公差也有双重职能：①控制几何误差；②协助控制尺寸误差。可逆要求用于最大实体要求的动态公差图，由于尺寸误差可以超差的缘故，其图形形状由直角梯形（最大实体要求）转为直角三角形（相当于在直角梯形的基础上加一个三角形），如图4-38（b）所示。

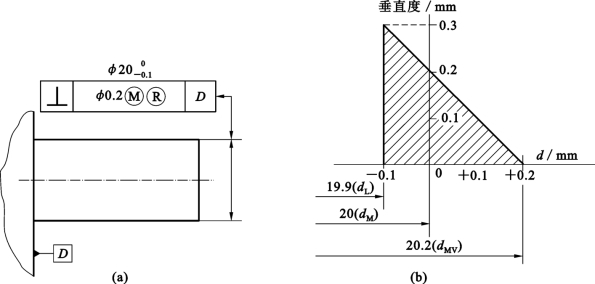
图4-38　可逆要求用于最大实体要求

（a）标注标记；（b）动态公差力

5）最大实体要求的实例分析

【例4-2】　对图4-34（a）做出解释。

解：①T、t标注解释。被测孔的尺寸公差为Th=0.13mm，DM=Dmin=φ50mm，DL=Dmax=φ50.13mm；在最大实体状态（φ50mm）下给定几何公差（垂直度）t1=0.08mm，当被测要素尺寸偏离最大实体状态的尺寸时，几何公差（垂直度）获得补偿，当被测要素尺寸为最小实体状态的尺寸φ50.13mm时，几何公差获得补偿最多，此时几何公差（垂直度）具有的最大值可以等于给定几何公差t1与尺寸公差Th的和，即tmax=0.08mm+0.13mm=0.21mm。

②动态公差图。T、t的动态公差图如图4-34（b）所示，图形形状为具有二直角的梯形。

③遵守边界。被测孔遵守最大实体实效边界MMVB，其边界尺寸为

④检验与合格条件。采用位置量规（轴型通规——模拟被测孔的最大实体实效边界）检验被测要素的体外作用尺寸Dfe，采用两点法检验被测要素的局部实际尺寸Da。其合格条件为

【例4-3】　对图4-36（a）做出解释。

解：①T、t标注解释如图4-36（a）所示，这是最大实体要求的零几何公差。被测孔的尺寸公差为Th=0.13mm，即DM=Dmin=φ50mm，DL=Dmax=φ50.13mm；在最大实体状态（φ50 mm）下给定被测孔轴线的几何公差（垂直度）t1=0，当被测要素尺寸偏离最大实体状态的尺寸时，几何公差获得补偿，当被测要素尺寸为最小实体状态的尺寸φ50.13mm时，几何公差（垂直度）获得补偿最多，此时几何公差（垂直度）具有的最大值可以等于给定几何公差t1与尺寸公差Th的和，即tmax=（0+0.13）mm=0.13mm。

②动态公差图。T、t的动态公差图如图4-36（b）所示，图形形状为直角三角形，恰好与包容要求的动态公差图形状相同。

③遵守边界。遵守最大实体实效边界MMVB，其边界尺寸为DMV=Dmin-t1=φ50mm-φ0mm=φ50mm，显然就是最大实体边界（因为给定的t1=0）。

④检验与合格条件。采用位置量规（轴型通规——模拟被测孔的最大实体实效边界）检验被测要素的体外作用尺寸Dfe，采用两点法检验被测要素的实际尺寸Da。其合格条件为Dfe≥φ50mm，φ50mm≤Da≤φ50.13mm。

【例4-4】　对图4-37（a）做出解释。

解：①T、t标注解释。由图4-37（a）可知，这是几何公差最大值受限的最大实体要求。尺寸公差为Th=0.13mm，即DM=Dmin=φ50mm，DL=Dmax=φ50.13mm；在最大实体状态下（φ50 mm）给定几何公差t1=0.08mm，并给定几何公差最大值tmax=0.12mm。当被测要素尺寸偏离最大实体状态的尺寸时，或当被测要素尺寸为最小实体状态尺寸φ50.13mm时，几何公差均可获得补偿。但最多可以补偿tmax与t1的差值，即0.12mm-0.08mm=0.04mm，几何公差（垂直度）具有的最大值就等于给定几何公差（垂直度）的最大值，即tmax=0.12mm。

②动态公差图。T、t的动态公差图如图4-37（b）所示，由于tmax=0.12mm，图形形状为具有三直角的五边形。

③遵守边界。遵守最大实体实效边界MMVB，其边界尺寸为DMV=Dmin-t1=φ50mm-φ0.08mm=φ49.92mm。

④检验与合格条件。采用位置量规（轴型通规，模拟被测孔的最大实体实效边界）检验被测要素的体外作用尺寸Dfe，采用两点法检验被测要素的实际尺寸Da，采用通用量具检验被测要素的几何误差（垂直度误差）f⊥。其合格条件为

【例4-5】　对图4-38（a）做出解释。

解：①T、t标注解释。图4-38（a）所示为可逆要求用于最大实体要求的轴线问题。轴的尺寸公差为Ts=0.1mm，即dM=dmax=φ20mm，dL=dmin=φ19.9mm；在最大实体状态下（φ20mm）给定几何公差t1=0.2mm，当被测要素尺寸偏离最大实体状态的尺寸时，几何公差获得补偿，当被测要素尺寸为最小实体状态的尺寸φ19.9mm时，几何公差获得补偿最多，此时几何公差具有的最大值可以等于给定几何公差t1与尺寸公差Ts的和，即tmax=0.2mm+0.1mm=0.3mm。

②可逆解释。在被测要素轴的几何误差（轴线垂直度）小于给定几何公差的条件下，即f⊥＜0.2mm时，被测要素的尺寸误差可以超差，即被测要素轴的实际尺寸可以超出极限尺寸φ20mm，但不可以超出所遵守的边界（最大实体实效边界）尺寸φ20.2mm。图4-38（b）中横轴的φ20～φ20.2mm为尺寸误差可以超差的范围（或称可逆范围）。

③动态公差图。T、t的动态公差图如图4-38（b）所示，其形状是三角形。

④遵守边界。遵守最大实体实效边界MMVB，其边界尺寸为dMV=dmax+t1=φ20mm+φ0.2mm=φ20.2mm。

⑤检验与合格条件。采用位置量规（孔型通规——模拟被测轴的最大实体实效边界）检验被测要素的体外作用尺寸dfe，采用两点法检验被测要素的实际尺寸da。

其合格条件为dfe≤φ20.2mm，φ19.9mm≤da≤φ20mm；当f⊥＜0.2mm时，φ19.9mm≤da≤φ20.2mm。

3.最小实体要求

1）最小实体要求的公差解释

最小实体要求也是相关公差原则中的三种要求之一，被测实际要素（关联要素）的实体（体内作用尺寸）遵循最小实体实效边界；被测实际要素的局部实际尺寸同时受最大实体尺寸和最小实体尺寸所限；几何公差t与尺寸公差Th（Ts）有关，在最小实体状态下给定几何公差（多为位置公差）值t1不为零（一定大于零，当为零时，是一种特殊情况——最小实体要求的零几何公差）；当被测实际要素偏离最小实体状态时，几何公差获得补偿，补偿量来自尺寸公差（被测实际要素偏离最小实体状态的量，相当于尺寸公差富余的量，可作补偿量），补偿量的一般计算公式为

当被测实际要素为最大实体状态时，几何公差获得补偿量最多，即t2max=Th（Ts），这种情况下允许几何公差的最大值为

几何公差t与尺寸公差Th（Ts）的关系可以用动态公差图表示，如图4-39（a）所示。由于给定几何公差值t1不为零，故动态公差图的图形一般为直角梯形。

2）最小实体要求的应用与检测

最小实体要求主要用于需要保证最小壁厚处（如空心的圆柱凸台、带孔的小垫圈等）的中心要素，一般是中心轴线的位置度、同轴度等。最小实体要求在零件图样上的标注是在几何公差框格的几何公差给定值t1后面加写，如图4-39（b）所示。

当基准（中心要素如轴线）也使用最小实体要求时，则在几何公差框格内的基准字母后面也加写。符合最小实体要求的被测实体（Dfi、dfi）不得超越最小实体实效边界LMVB；被测要素的局部实际尺寸（Da、da）不得超越最大实体尺寸MMS和最小实体尺寸LMS。目前尚没有检验用量规，因为按最小实体实效尺寸判定孔、轴体内作用尺寸的合格性问题，在于量规无法实现检测过程（量规测头不可能进入被测要素的体内。生产中一般采用通用量具检验被测实际要素的体内作用尺寸（Dfi、dfi）是否超越最小实体实效边界，即测量足够多点的数据，绘图法（在测量具备很好条件时，使用坐标机测量并由计算机处理测量数据更好）求得被测要素的体内作用尺寸（Dfi、dfi），再判定其是否超越最小实体实效边界LMVB，不超越为合格；被测实际要素的局部实际尺寸（Da、da）按两点法测量，以判定是否超越最大实体尺寸和最小实体尺寸，局部实际尺寸落入极限尺寸内为合格。符合最小实体要求的被测实际要素的合格条件如下。

图4-39　最小实体要求

（a）标注；（b）动态公差图

对于孔（内表面）：　　　Dfi≤DLV=Dmax+t1；Dmin=DM≤Da≤DL=Dmax

对于轴（外表面）：　　　dfi≥dLV=dmin-t1；dmax=dM≥da≥dL=dmin

3）最小实体要求的零几何公差

这是最小实体要求的特殊情况，允许在最小实体状态时给定位置公差值为零。在零件图样上的标注标记是在位置公差框格的第二格内，即位置公差值的格内写0（φ0），如图4-36（a）所示。此种情况下，被测实际要素的最小实体实效边界就变成了最小实体边界。对于位置公差而言，最小实体要求的零几何公差比起最小实体要求来，显然更严格。图4-40（b）是图4-40（a）的动态公差图，其形状为直角三角形。动态公差图的形状恰好与同类要素的最大实体要求的零几何公差的动态公差图形状（见图4-36（b））相同，但斜边的方向相反（镜像关系）。

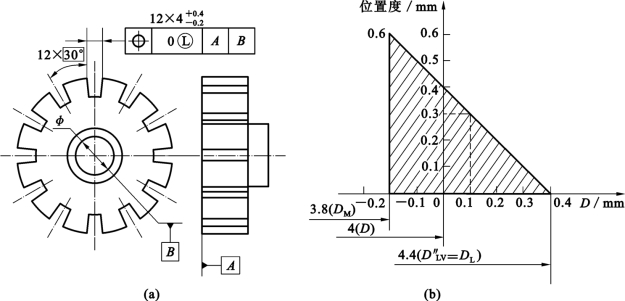
图4-40　最小实体要求的零几何公差

（a）标注；（b）动态公差图

4）可逆要求用于最小实体要求

在不影响零件功能的前提下，位置公差可以反过来补给尺寸公差，即位置公差有富余的情况下，允许尺寸误差超过给定的尺寸公差，显然在一定程度上能够降低工件的废品率。在零件图样上，可逆要求用于最小实体要求的标注标记是在位置公差框格的第二格内位置公差值后面加写，如图4-41（a）所示。此时尺寸公差有双重职能：①控制尺寸误差；②协助控制几何误差。而位置公差也有双重职能：①控制几何误差；②协助控制尺寸误差。图4-41（a）所示的槽位置度，其可逆要求用于最小实体要求的动态公差图，如图4-37（b）所示，图中横轴（槽宽尺寸）上4.2～4.4 mm即为槽宽尺寸可以超差的范围（注意：只当位置度误差小于0.2mm时有效）。可逆要求用于最小实体要求的动态公差图，其形状由直角梯形（最小实体要求的动态公差图）转为直角三角形（在直角梯形的直角短边处加一三角形）。

图4-41　可逆要求用于最小实体要求

（a）标注；（b）动态公差图

5）最小实体要求的实例分析

【例4-6】　对图4-39（a）做出解释。

解：①T、t标注解释。被测槽宽的尺寸公差Th=0.4 mm，DM=Dmin=3.8 mm，DL=Dmax=4.2mm；在最小实体状态下给定几何公差（位置度）t1=0.2mm，当被测要素尺寸（槽宽）偏离最小实体状态的尺寸4.2mm时，几何公差位置度获得补偿，当被测要素尺寸为最大实体状态的尺寸3.8mm时，几何公差位置度获得补偿最多，此时几何公差具有的最大值可以等于给定几何公差t1与尺寸公差Th的和，即

②动态公差图。T、t的动态公差图如图4-39（b）所示，图形形状为具有二直角的梯形。

③遵守边界。遵守最小实体实效边界LMVB，其边界尺寸为

④判断合格条件。被测要素的体内作用尺寸Dfi和局部实际尺寸Da的合格条件为

【例4-7】　对图4-40（a）做出解释。

解：①T、t标注解释。如图4-40（a）所示，这是最小实体要求的零几何公差。被测槽宽的尺寸公差Th=0.6mm，DM=Dmin=3.8 mm，DL=Dmax=4.4 mm；在最小实体状态下（4.4 mm）给定几何公差（位置度）t1=0，当被测要素尺寸偏离最小实体状态时，几何公差获得补偿，当被测要素尺寸为最大实体状态的尺寸3.8mm时，几何公差（位置度）获得补偿最多，此时几何公差具有的最大值可以等于给定几何公差t1与尺寸公差Th的和，即

②动态公差图。T、t的动态公差图如图4-40（b）所示，图形形状为直角三角形。

③遵守边界。遵守最小实体实效边界LMVB，其边界尺寸为

显然就是最小实体边界（因为给定的t1=0）。

④合格条件。被测要素的体内作用尺寸Dfi和局部实际尺寸Da的合格条件为

【例4-8】　对图4-41（a）做出解释。

解：①T、t标注解释。图4-41（a）所示为可逆要求用于最小实体要求的槽的位置度问题。槽宽的尺寸公差为Th=0.4mm，即DM=Dmin=3.8mm，DL=Dmax=4.2mm；在最小实体状态下（4.2mm）给定位置度公差t1=0.2mm，当被测要素尺寸（槽宽的尺寸）偏离最小实体状态的尺寸时，位置度公差获得补偿，当被测要素尺寸为最大实体状态的尺寸3.8mm时，位置度公差获得补偿最多，此时位置度公差具有的最大值可以等于给定位置度公差t1与尺寸公差Th的和，即tmax=0.2mm+0.4mm=0.6mm。

②可逆解释。在被测要素槽的位置度误差小于给定位置度公差的条件下，即f＜0.2 mm时，被测要素槽的尺寸误差可以超差，即被测要素槽的实际尺寸可以超出极限尺寸4.2 mm，但不可以超出所遵守边界的尺寸4.4mm。图4-41（b）中横轴的4.2～4.4为槽的尺寸误差可以超差的范围（或称可逆范围）。

③动态公差图。T、t的动态公差图如图4-41（b）所示，其形状是三角形。

④遵守边界。遵守最小实体实效边界LMVB，其边界尺寸为

⑤合格条件。被测要素的体内作用尺寸Dfi和被测要素的局部实际尺寸Da。其合格条件为

当f＜0.2mm时，3.8mm≤da≤4.4mm

综上所述，公差原则是解决生产第一线中尺寸误差与几何误差关系等实际问题的常用规则。但由于相关原则的术语、概念较多，各种要求适用范围迥然不同，补偿、可逆、零公差、动态公差图等都是前面几章所未有的，再加上几何公差的问题本来就较尺寸公差的复杂，不免难以学透、不易用好。相关公差原则的三种要求的比较如表4-10所示。

表4-10　相关公差原则三种要求的比较

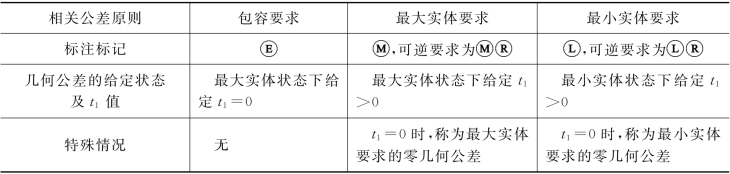
续表

任务实施

图4-29各图遵守的公差原则及图样解释：

（1）独立原则。

实际尺寸的合格范围是φ19.979mm～φ20mm，不受轴线直线度公差带控制；轴线的直线度误差不大于φ0.05mm，不受尺寸公差带控制。

（2）最大实体要求。

①轴的任一局部实际尺寸在φ19.979mm～φ20mm之间。

②实际轮廓不超出最大实体实效边界，最大实体实效尺寸为dMV=dm+t=20 mm+0.05mm=20.05mm。

③当该轴处于最小实体状态时，其轴线的直线度误差允许达到最大值，即尺寸公差值全部补偿给直线度公差，允许直线度误差为φ0.021mm+φ0.05mm=φ0.071mm。

（3）零几何公差。

①轴的任一局部实际尺寸在φ19.979mm～φ20mm之间。

②实际轮廓不超出最大实体边界，最大实体尺寸为dm=20mm。

③当该轴处于最小实体状态时，允许直线度误差为φ0.021mm。

若中间图加工后测得零件尺寸为φ19.985mm，且垂直度误差为φ0.06mm时，则机件合格。因为尺寸在φ19.979mm～φ20mm之间，允许直线度误差为φ0.015mm+φ0.05mm=φ0.065mm。