图6.21纽约市每日犯罪折线图图6.22纽约市每月犯罪箱线图用离散点的形式描述抗议事件不能充分体现其空间分布趋势，可采用核密度估计方法。为研究“弗洛伊德事件”发生后纽约市犯罪事件的空间分布变化，对犯罪事件进行核密度分析以及平均最近邻分析。......
2023-06-15
空间相关性分析：方法与应用
【摘要】：图6.25入室盗窃犯罪数量分时间分区域统计图为探明哪些社会经济指标对抗议事件的发生有影响，哪些指标的影响是正面的，哪些指标的影响是负面的，本研究使用了栅格数据相关性分析方法。图6.27栅格相关性分析矩阵由于相关矩阵的对称性，可以用三角矩阵的形式描述相关性。
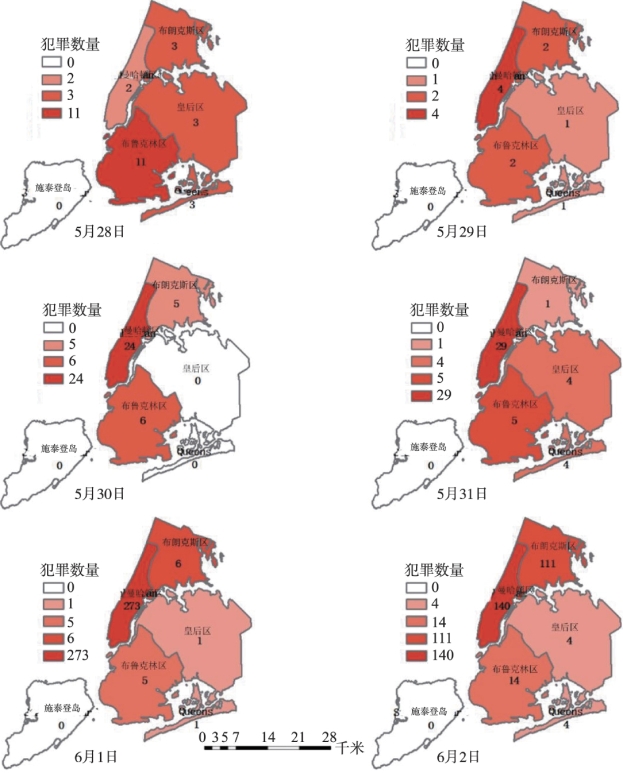
图6.25 入室盗窃犯罪数量分时间分区域统计图
为探明哪些社会经济指标对抗议事件的发生有影响，哪些指标的影响是正面的，哪些指标的影响是负面的，本研究使用了栅格数据相关性分析方法。由于矢量数据难以进行全局尺度的相关性分析，因此将全美经济指标矢量数据转换为栅格形式，对它们及抗议事件栅格合计35种指标栅格数据，用相关矩阵描述指标间的相关性。
图6.26 入室盗窃事件平均最近邻分析结果
为计算相关矩阵，需要计算协方差矩阵，协方差矩阵的对角线元素是方差，表示图层中每个像元数值相对于该图层平均值的差异，其他位置的元素则是协方差，表示不同图层间的相关性，协方差的计算公式为:
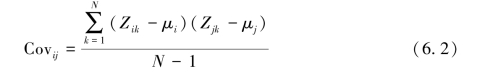
式中，i，j分别表示参与运算的两个图层；k表示特定的像元；Z表示像元数值；N表示图层中像元个数，μ表示图层像元的平均数值。
协方差矩阵的数值取决于数值的单位，相关矩阵则消去了单位的影响，相关矩阵中元素的计算公式为:
式中，Covij表示两个图层的协方差；δ为图层的标准差。
相关性的值域是[－1，1]，相关性取值为正表示两图层有正向的相关性，即一个图层某位置的指标较大时，另一图层相同位置指标也较大。负相关则正好相反，表示负向的相关性，随着相关性取值的绝对值增大，相关性也越来越明显。相关性取值趋于0时，表明两个图层不存在相关关系。将相关矩阵以色块图的形式进行可视化，结果如图6.27所示。
图6.27 栅格相关性分析矩阵
由于相关矩阵的对称性，可以用三角矩阵的形式描述相关性。结果表明:与抗议强度正向相关性最高的因素分别是就业人数、人均收入偏差、平均通勤时间、私人工作方式、总人口数、成年人数，以及女性人数。一般来说，这些相关性较高的区域也是城市化程度较高的区域，与传统认知相符。与抗议强度负向相关性最高的因素包括建筑业从业占比、人均收入、太平洋岛人、公共工作方式以及步行通勤方式。建筑业从业占比和人均收入两项因素与传统认知不符，或许反映了美国城市发展更为均衡的特点，太平洋岛人由于在各地区占比较低，可能存在偶然性，公共工作方式和步行通勤方式则代表着生活相对平稳的非城市区，与抗议活动主要发生在大都市区的推断相符。
有关应急大数据的空间分析与多因素关联挖掘的文章
- 详细阅读
-
线性空间同构证明及相关性质详细阅读
，σ（αn）是线性无关的.因此，n≤m.综合上面的结论可以得到n=m，即V1，V2有相同的维数.充分性.设V1，V2都是n维线性空间，下面我们来建立一个从V1到V2的同构映射，从而证明V1V2.分别取V1的一组基α1，α2，…，αn之下的坐标是唯一确定的，而向量组β1，β2，…......
2023-11-22
-
线性相关性分析方法简介详细阅读
相关性分析可以分为线性相关分析、偏相关分析、距离分析等。对交通事故与相关要素之间相关性进行计算时，由于数据不符合正态分布，所以选择Kendall相关系数、Spearman相关系数分析计算，得到Kendall及Spearman相关系数分析结果见表4.3，依次表示事故伤亡等级、日夜、季节、假期、风速、温度、天气、酒精、车速、大型车辆之间的相关系数和显著性。表4.3Kendall及Spearman相关系数分析结果......
2023-06-15
-
空间自相关分析方法介绍详细阅读
莫兰指数I用标准化统计量Z来检验n个区域是否存在空间自相关关系，当Z值为正且显著时，表明存在正的空间自相关；当Z值为负且显著时，表明存在负的空间自相关，相似的观测值趋于分散分布；当Z值为零时，观测值呈独立随机分布。交通事故发生率的莫兰指数I为0.28，G观测值为0.001126，表明交通事故发生率具有强烈的空间相关性、聚集性，即某地的交通事故与该地区的位置有关。图3.21局部莫兰指数......
2023-06-15
-
桥梁抽样方法分析-桥梁可靠度分析方法与应用详细阅读
一般的MC法用于高度非线性的极限状态曲面或者随机变量维数较高的情况，使用在笛卡儿坐标下的抽样模拟法效率较低，计算耗时较多。因此，Ditlevsen、Olesen、Mohr提出了在标准正态空间中极坐标下进行抽样的方向抽样MC法。③重复步骤①和②直到N次，利用式估计失效概率。对于极限状态曲面接近球面的情况，方向抽样MC法比笛卡尔坐标空间的MC法占较大的优势，若计算接近平面的极限状态曲面时，则无优势。......
2023-09-19
-
物相衍射分析方法与应用详细阅读
对于混合物来说，各个晶相的衍射花样会同时出现，而不会出现干涉。X射线物相分析可以鉴别样品中的物相，包括纯元素（单质）、化合物和固溶体。同一种材料，可以具有不同的物相，称为同分异构体。就广义而言，物相衍射分析包括物相鉴定、定量分析、相结构的测定以及相变过程检测等。但对于纳米材料，晶粒的小尺寸会导致衍射峰的宽化，进而影响积分强度的计算，所以纳米材料定量分析的精度和准确度都远低于传统材料。......
2023-06-20
-
应急大数据的空间分析方法详细阅读
应急大数据的时空分析从地理空间位置和时间的角度分析了突发事件的演变情况，按照时间尺度的长短可以分为长期发生规律和短期内突发事件发展过程研究；根据空间范围的大小则可以分为大、中、小尺度的分布特性、发展趋势研究。国内发表的论文主要研究内容包括灾害时空变化、空间格局和影响因素。......
2023-06-15
-
Stevens论述的GRTS空间抽样方法及应详细阅读
Stevens 对该抽样方法进行了详细的描述[8]，并应用于河谷流域的水资源和生物资源调查。严格来说，这不是一种简单布样方式。GRTS 空间构造布设站位可以分为3 步（见图1）：第1 步将空间划分，不断重复这个过程直到最小单位为1 个单元格；第2 步对空间中划分得到的格网编码，转换为一维序列；第3 步按照采样点数量计算抽样步长，并进行抽样。......
2023-11-17
相关推荐