而在5220m至5560m的距离下，抢劫事件的空间网络K函数值开始减少并逐渐小于蒙特卡洛模拟下限曲线值，说明在5220m及以上的距离上，抢劫事件逐渐表现出空间均匀分布的特征。图6.4抢劫事件时空网络K函数对于盗窃事件，用2017年纽约市发生盗窃事件共计147489起进行分析，图6.5为对应的分析结果，图中各项含义与图6.3相同。......
2025-09-29
空间分布分析：方法与应用
【摘要】：图6.21纽约市每日犯罪折线图图6.22纽约市每月犯罪箱线图用离散点的形式描述抗议事件不能充分体现其空间分布趋势，可采用核密度估计方法。为研究“弗洛伊德事件”发生后纽约市犯罪事件的空间分布变化，对犯罪事件进行核密度分析以及平均最近邻分析。
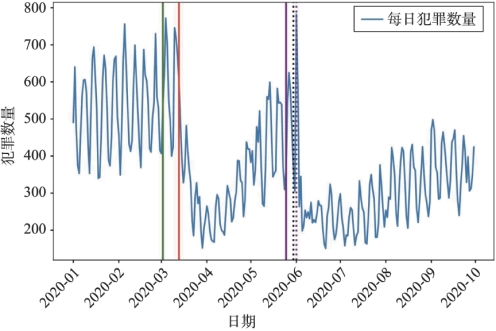
图6.21 纽约市每日犯罪折线图
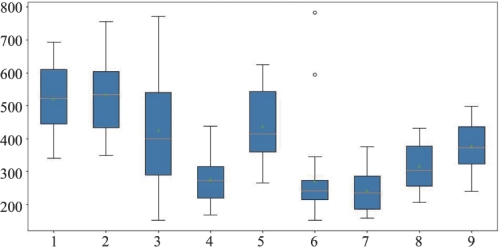
图6.22 纽约市每月犯罪箱线图
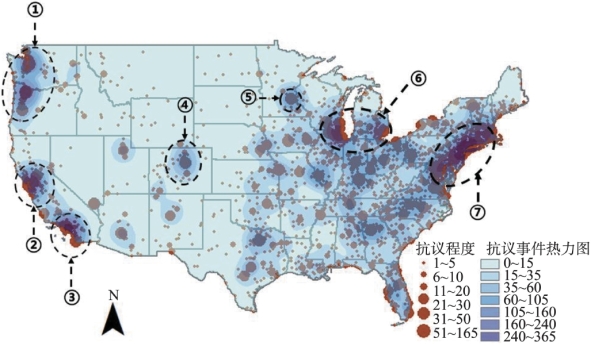
用离散点的形式描述抗议事件不能充分体现其空间分布趋势，可采用核密度估计方法。核密度估计是一种基于非参数估计的空间数据描述方法，它将研究区域格网化，通过定义核函数，计算样本点落入每个格网的概率来计算目标数据的空间分布；表现形式方面，它将点状空间要素转化为面状要素，用不同颜色区分不同格网中数据的分布概率。用核密度估计方法处理抗议事件空间位置数据，得到如图6.24所示结果，图6.24中蓝色的面状要素为核密度估计的结果，红色的点状要素是以频次作为权重的抗议事件的严重程度。
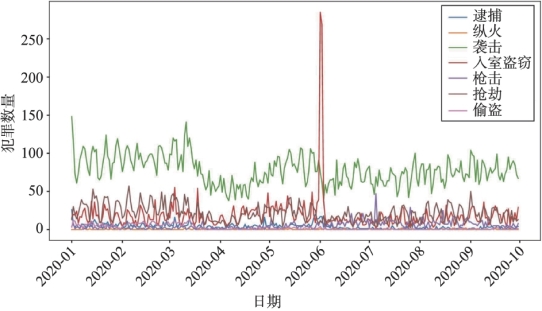
图6.23 纽约市不同类型犯罪折线图
(https://www.chuimin.cn)
图6.24 美国本土抗议事件空间分布
从分布趋势可以看出，群体性抗议事件呈现出明显的空间聚集效应:它们更多地出现在美国本土东部；而在西部，它们则主要集中于西海岸地区。核密度估计目视判读的结果表明，美国的大都市区一般是抗议活动程度较高的区域，从中能够提取出7个有代表性的抗议事件聚集中心，如图6.24所示，它们分别是:以西雅图和俄勒冈为中心的区域①；以旧金山为中心的区域②；以洛杉矶为中心的区域③；以丹佛为中心的区域④；以明尼阿波利斯为中心的区域⑤；以芝加哥、密尔沃基、底特律为中心的区域⑥；以及以纽约都市圈为中心的区域⑦。
为研究“弗洛伊德事件”发生后纽约市犯罪事件的空间分布变化，对犯罪事件进行核密度分析以及平均最近邻分析。由于在各个犯罪类型中只有入室盗窃犯罪数据在“弗洛伊德事件”爆发后产生了极大的波动性，因此在此研究中只分析入室盗窃犯罪的空间变化。
利用自然间断点分类法对研究区入室盗窃犯罪事件进行分类标注，如图6.25所示，入室盗窃犯罪事件数量在各区分布十分不均，从集中在布鲁克林区(5月28日)演变至集中于曼哈顿区，在6月1日时曼哈顿区数量超过200次，而其他地区均在10次以下，在6月2日时集中分布于曼哈顿区和布朗克斯区(均为100次以上)。
采用平均最近邻分析(ANN)模型研究抗议期间犯罪事件的空间集中度和犯罪分布，ANN比率计算公式为:
如果ANN值小于1，则表示数据呈现聚集模式；如果ANN值大于1，则表示数据呈现分散模式。在利用平均最近邻分析时，会得到数据统计显著性的量度p值、z得分，用来判断是否拒绝零假设。对纽约市5月20日至6月10日的入室盗窃犯罪数据进行平均最近邻分析，得到每日犯罪数据的ANN比率以及p值，如图6.26所示，红色条带为ANN值，蓝色条带为p值。从图中分析可知在5月29日之前，空间分布状态为波动状态；从5月30日开始ANN值均小于1，且p值和z值得分值均为0，入室盗窃犯罪呈现明显的聚集状态；到6月5日恢复到离散模式，后又回到波动状态。
相关文章
- 详细阅读
-
应急大数据的空间分析方法详细阅读
应急大数据的时空分析从地理空间位置和时间的角度分析了突发事件的演变情况，按照时间尺度的长短可以分为长期发生规律和短期内突发事件发展过程研究；根据空间范围的大小则可以分为大、中、小尺度的分布特性、发展趋势研究。国内发表的论文主要研究内容包括灾害时空变化、空间格局和影响因素。......
2025-09-29
-
暂态电势与电抗的分析与应用详细阅读
图9-9暂态电势和暂态电抗的等值电路习惯上称E′q为暂态电势，它同励磁绕组的总磁链Ψf成正比。电势正比于磁链，由此可见，暂态电势E′q也是某种意义下的气隙电势，暂态电抗x′d则是某种意义下的定子漏抗。如果令便可将方程式改写成电势常称为暂态电抗后的电势。以上根据磁链平衡方程式导出了暂态电势和暂态电抗的表达式，并对这些参数的意义作了说明。暂态电势在运行状态发生突变瞬间能够守恒。......
2025-09-29
-
空间探索分析技巧详细阅读
图3.6MN17区交通事故的空间分布特征一组数据点在空间上的聚集性和方向性可以用标准差椭圆来描述。通过计算，得到MN17区交通事故点的平均最邻近距离为2.25 m，计算事故点之间的平均时间间隔为6.63小时。采用置信度为95%的统计显著性对结果进行判断，结果表明，MN17区的交通事故具有时空聚集性和显著的时空交互性，即交通事故在时间上也呈现出聚集模式。......
2025-09-29
-
主成分分析原理与方法详细阅读
主成分分析法的主要优点包括:①可消除评估指标之间的相关影响。对于其他评估方法，由于难以消除评估指标间的相关影响，所以选择指标时要花费较多精力，而主成分分析法可以消除这种相关影响，所以在指标选择上相对容易些。对纽约交通事故进行主成分分析，从分析结果可以看出，KMO取样适宜性数量为0.491，巴特利特球形度检验的近似卡方值为1533.013，自由度为36，显著性小于0.001。表4.2旋转后的成分矩阵......
2025-09-29
-
纽约市交通事故密度分析与分布详细阅读
图3.14纽约市路网和2020年交通事故分布情况为便于比较，对密度数据进行归一化处理，采用“几何间隔”分类方案对所得密度值进行分类。图3.15为纽约市交通事故的密度分布图，分别采用了点密度分析和核密度分析的方法，颜色越深的区域代表事故密度越大。将事故造成的伤亡情况加权，得到密度分析结果，如图3.16所示，其中图为点密度分析结果，图为核心密度分析结果。图3.15纽约市交通事故密度分布图图3.16交通事故严重程度的密度图......
2025-09-29
-
多准则决策分析的优化方法详细阅读
多准则决策分析主要包括数据准备及预处理、缓冲区分析、缓冲区域分级权重赋值、按权重叠置分析、输出结果专题地图等步骤。图3.26纽约市消防站负荷状况从数学的角度，缓冲区定义为给定一个空间对象或集合，确定其邻域，邻域半径即缓冲距离(宽度)，是缓冲区分析的主要数量指标，可以是常数或变量。按照表3.12的划分依据，通过叠置分析将服务区划分为低值区、中值区、高值区三个等级，从而得到纽约市医院空间布局优化图。......
2025-09-29
-
闭式网潮流分布计算方法详细阅读
在求出闭式网络中的初步功率分布后，还必须计算网络中各段的电压和功率损耗，方能获得潮流分布计算的最终结果。从闭式网络的初步功率分布可以看出，某些节点的功率是由两侧向其流入的，这种节点称为功率分点，并用符号“▼”标出，如有功、无功功率分点不一致，则以“▼”、“▽”分别表示有功功率、无功功率分点。......
2025-09-29
相关推荐