犯罪事件空间分布模式的分析与优化

2023-06-15 历史故事版权反馈

【摘要】：而在5220m至5560m的距离下，抢劫事件的空间网络K函数值开始减少并逐渐小于蒙特卡洛模拟下限曲线值，说明在5220m及以上的距离上，抢劫事件逐渐表现出空间均匀分布的特征。图6.4抢劫事件时空网络K函数对于盗窃事件，用2017年纽约市发生盗窃事件共计147489起进行分析，图6.5为对应的分析结果，图中各项含义与图6.3相同。

犯罪事件的空间分布模式分析使用了时空网络K函数分析，它可分为以下两步展开:对单类型的犯罪事件，分别进行网络K函数分析和时间K函数分析，获得各类型犯罪事件分别在网络空间维度和时间维度的分布模式，再结合时空网络K函数，分析各类型犯罪事件的时空分布模式；对多类型的犯罪事件关系，进行交叉K函数分析，研究在相同时段内不同类型犯罪的分布模式间是否存在相互影响，若存在相互影响则对其影响关系和可能的原因进行解释。

1.单类型犯罪事件时空分布模式分析

用纽约市犯罪数和道路网数据，分别对抢劫事件、盗窃事件和暴力犯罪事件采用空间网络K函数、时间K函数和时空网络K函数方法，计算不同的犯罪类型在空间维度、时间维度和时空维度的分布模式，得到以下结论:

对纽约市14005起抢劫事件进行分析，图6.3为空间网络K函数与时间K函数分析的结果。图中给出了抢劫事件的实际K函数曲线、随机分布的K函数期望值曲线、显著性水平为0.05时蒙特卡洛模拟的上限和下限，横轴表示空间网络距离，纵轴表示K函数值。

pagenumber_ebook=151,pagenumber_book=144

图6.3　抢劫事件空间与时间分布模式分析

从图6.3(a)可以看出，抢劫事件的空间网络K函数曲线在0～5220m的空间网络距离下是位于蒙特卡洛模拟的上限之上，并在距离为3800m处网络空间K函数曲线与蒙特卡洛模拟上限曲线的差异达到最大值，说明在距离为0～5220m时抢劫事件表现出空间聚集性且在距离为3800m时抢劫事件的空间聚集性表现最明显。而在5220m至5560m的距离下，抢劫事件的空间网络K函数值开始减少并逐渐小于蒙特卡洛模拟下限曲线值，说明在5220m及以上的距离上，抢劫事件逐渐表现出空间均匀分布的特征。

由图6.3(b)可见，抢劫事件的时间K函数曲线仅在时间间隔为0～4.5天时位于蒙特卡洛模拟上限之上；在4.5天及以上的时间间隔上，时间K函数曲线完全位于蒙特卡洛模拟的置信区间内，因此抢劫事件在时间间隔为4.5天以内是表现出时间聚集性的，而在4.5天以上的时间间隔上是完全符合时间随机分布的。

图6.4为采用时空网络K函数方法对抢劫事件分析的结果，图中K(d，t)轴表示时空网络K函数值，空间距离其单位为m，采用了0.01天作为时间单位。结果显示，在指定空间距离即d值确定的条件下，K(d，t)随时间间隔t的增长而增加且增长趋势稳定，该现象符合时间K函数的分析结果。在指定时间间隔即t值确定的条件下，当空间网络距离小于4300m时，K(d，t)值随空间距离d的增长而增长且增长趋势稳定；而在空间网络距离小于4300m且时间间隔大于37天时，发现K(d，t)出现了减少的趋势，结合在空间网络K函数分析中的发现即在距离为4300m至4800m时，K(d)值出现了下降又上升的变化，由此可知，空间网络K函数分析时出现该现象的时间间隔为大于37天。综合而言，抢劫事件的时空网络K函数值在0～4300的空间网络或0～37天的时间间隔上是持续增长的，在该时空范围内抢劫事件表现了较强的时空聚集性；而在4300m至4800m的空间距离且37天以上的时间间隔时，该值出现了先下降而后上升的现象，说明在该时空范围内，抢劫事件的时空聚集度波动较大。

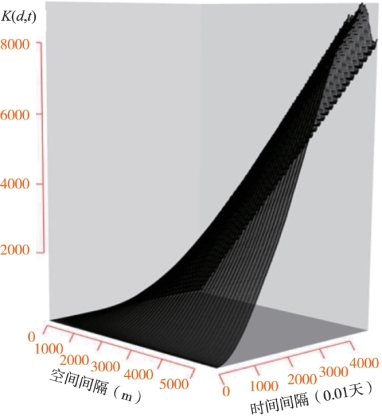
pagenumber_ebook=152,pagenumber_book=145

图6.4　抢劫事件时空网络K函数

对于盗窃事件，用2017年纽约市发生盗窃事件共计147489起进行分析，图6.5为对应的分析结果，图中各项含义与图6.3相同。由图6.5(a)可得，盗窃事件的空间网络K函数曲线始终在蒙特卡洛模拟上限曲线之上，在0～700m的空间距离上，空间网络K函数曲线增长较缓，而在700m至1800m的网络距离上空间网络K函数曲线增长速度加快且保持稳定的增长速度，说明盗窃事件在空间分布上表现出较高的聚集性。在0～700m的距离上盗窃事件的空间聚集性增长较缓，在大于700m的距离上，随空间网络距离的增长空间聚集性变得更明显，而在空间网络距离为1800m时空间聚集度最高，超过1800m后空间聚集度有所降低。图6.5(b)所展示的时间K函数曲线表明，时间K函数曲线完全位于由蒙特卡洛模拟上限曲线和下限曲线构建的包络线内，因此盗窃事件的时间分布完全符合均匀分布。

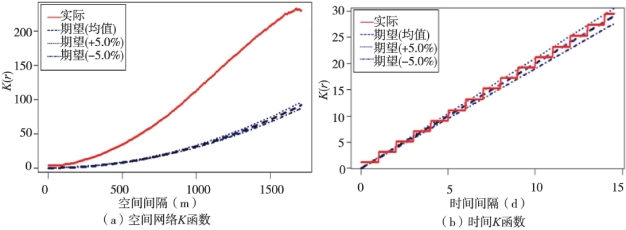
pagenumber_ebook=153,pagenumber_book=146

图6.5　盗窃事件空间与时间分布模式分析

图6.6为盗窃事件的时空网络K函数分析结果，由图可见盗窃事件的时空网络K函数曲线值随时间间隔和空间网络距离的增大而增加，是完全符合空间网络K函数与时间K函数分析结果的，因此盗窃事件因空间分布呈聚集性而表现出时空聚集性且其时空聚集度随空间距离的增大而增加。

对70918起暴力犯罪事件进行分析，图6.7为对应的分析结果，图中各项含义与图6.3相同。由图6.7(a)可见，暴力犯罪事件的空间网络K函数曲线处于蒙特卡洛模拟的上限曲线以上，且随着空间网络距离的增长而不断上升，其上升速度也逐渐加快，与蒙特卡洛上限曲线间差值逐渐增大，这说明暴力犯罪事件在空间中呈聚集分布且其聚集性随空间网络距离的增加而增大。图6.7(b)中曲线位置及变化趋势与图6.5(b)相同，因此暴力犯罪事件在时间维度中的分布也是呈均匀分布的。

图6.8为暴力犯罪事件的时空网络K函数分析结果，由图可知，暴力犯罪事件的时空网络K函数值随时间和距离的增长而增加，符合空间K函数与时间K函数的分析结果，故其表现出时空聚集性且其时空聚集性随空间距离的增大而变得更明显。

综合对三类犯罪事件的时空网络K函数分析，抢劫事件在空间网络距离小于5220m时表现出空间聚集性且在3800m时空间聚集度最高；在时间间隔小于4.5天时表现出时间聚集性而其他时间间隔条件下则呈均匀分布；盗窃事件和暴力犯罪事件在空间上均呈聚集分布，盗窃事件在距离为1800m时空间聚集度最高而暴力犯罪事件空间聚集度随距离增大而不断增加，两类犯罪事件在时间上均呈均匀分布。

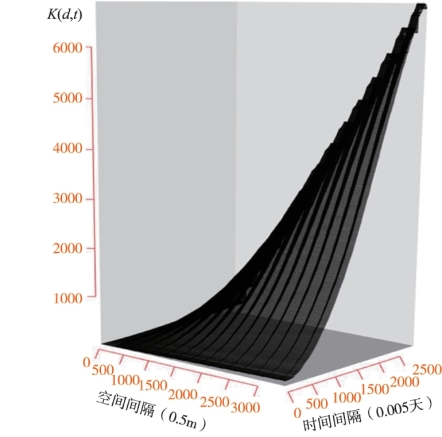
pagenumber_ebook=154,pagenumber_book=147

图6.6　盗窃事件时空网络K函数

pagenumber_ebook=154,pagenumber_book=147

图6.7　暴力犯罪事件空间和时间分布模式分析

pagenumber_ebook=155,pagenumber_book=148

图6.8　暴力犯罪事件时空网络K函数

2.多类型犯罪事件时空分布模式关系分析

盗窃事件和暴力犯罪事件的交叉网络K函数曲线如图6.9所示。各项含义同图6.5。从图中可以看出，K函数曲线自200m左右开始位于蒙特卡洛模拟的上限曲线之上，这表明在盗窃事件发生的区域附近，暴力犯罪事件表现出空间聚集性，而且随着空间网络距离的增加，盗窃事件的分布与暴力犯罪事件的分布之间表现出更显著的聚集关系。随着空间网络距离的增大，K函数曲线保持稳定的增长趋势且与CSR随机模式的期望值曲线间差值增加，这说明随着空间网络距离的增加，盗窃事件与暴力犯罪事件间的空间聚集关系表现更明显。在空间距离约2000m处，K函数曲线出现了短暂的下降现象，说明在空间距离2000m处盗窃事件与暴力犯罪事件的空间聚集度有轻微减少，但并不影响其整体的显著空间聚集特性。

盗窃事件和抢劫事件的交叉网络K函数曲线如图6.10所示，各项含义同图6.5。从图中可以看出，在空间网络距离为300m至5270m时，K函数曲线是完全位于蒙特卡洛模拟的上限曲线之上，在距离为300m至4900m间，K函数曲线持续上升，其与CSR随机模式的期望值曲线差值在4320m取得最大值，而在4900m至5550m间K函数值曲线持续下降，在约5370m处K函数值曲线降到CSR随机模式的期望值曲线之下。因此，在空间网络距离为300m至5270m时，在盗窃事件发生的区域附近，抢劫事件表现出了空间聚集性，且在4320m处空间聚集性较为显著，而自4900m处开始空间聚集性逐渐降低并逐步变为空间随机分布。

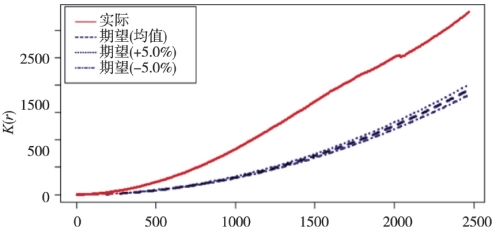
pagenumber_ebook=156,pagenumber_book=149

图6.9　盗窃事件与暴力犯罪事件的交叉网络K函数

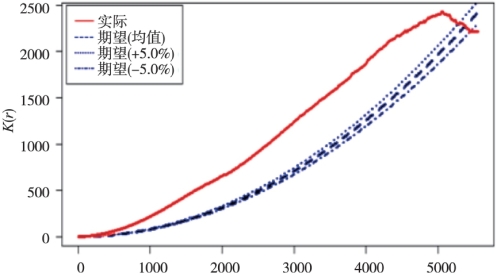
pagenumber_ebook=156,pagenumber_book=149

图6.10　盗窃事件与抢劫事件的交叉网络K函数

暴力犯罪事件与抢劫事件的交叉网络K函数曲线如图6.11所示。各项含义同图6.5。图6.11与图6.9的曲线形状类似，K函数曲线均为先增后减。在0至4900m左右时，K函数曲线持续上升，而在4900m后K函数曲线持续下降，并在约5300m处下降至CSR随机模式的期望曲线以下，K函数曲线与蒙特卡洛模拟的上限曲线间最大差值在约4000m处取得。因此，在空间网络距离为200m至5300m时，发生暴力犯罪事件区域附近的抢劫事件呈空间聚集分布，其空间聚集性在空间网络距离为4000m处最为显著，而在距离为4900m之外其空间聚集度持续降低并于5300m外呈空间随机分布。

pagenumber_ebook=157,pagenumber_book=150

图6.11　暴力犯罪事件与抢劫事件的交叉网络K函数

综合分析三类犯罪事件空间分布模式间的关系，盗窃事件与暴力犯罪事件间的空间聚集关系最为明显，且随空间网络距离增大而变得更为显著，盗窃事件与抢劫事件及暴力犯罪事件与抢劫事件间的空间聚集度稍弱且均在约5000m的空间网络距离内表现出空间聚集关系，而在5000m外则呈空间随机分布。

犯罪事件空间分布模式的分析与优化

相关推荐