另外，随机森林法可以评价各种指标的重要程度。装袋算法通过自助抽样法有效地提高了随机森林算法的准确度。Breiman在1984年提出的分类回归树是一种不稳定的学习算法，因此CART方法与装袋算法结合就形成了随机森林算法，可以提高模型预测准确率。随机森林模型中某一特征的重要性，是所有决策树得到的该特征重要性的平均值。......
2023-06-15
SIR模型及其扩展原理详解
【摘要】：图5.14SIR模型(上)和SEIR模型(下)各仓室人群流动图每个感染者都具有传染力，当他们与易感人群接触时，就有可能将疾病传染给易感者，接触率与总人口数成正比。通过起始值、时间值等参数设置，根据SIR模型的假设和反映移动规律的微分方程，可以模拟出在一段时间内各个仓室人群的人口变化规律。计算伪代码如算法5.1所示:算法5.1SIR模型
利用数学模型来了解传染病动力学有着非常丰富的历史。在1927年，Kermack和McKendrick在他们开创性的论文中介绍了S(易感者)－I(感染者)－R(康复者)模型，并提出了用于此标准的SIR模型的常微分方程组的一系列严格假设(Bartlett M S，1958)。经典的SIR模型是一种基于严格假设的模型，假设人口中出生率和自然死亡率相等，且不考虑种群的迁入、迁出等人口流动因素，假设在该模型中可以忽略由疾病导致的死亡率，即只考虑发病率而不考虑致死率，这些假设都是为了营造一个封闭的传染病模型，即模型中的总人口数不变。同一类人群划分为一个仓室，每个仓室的人群，以一定的规律在各个仓室之间移动，如图5.14所示。
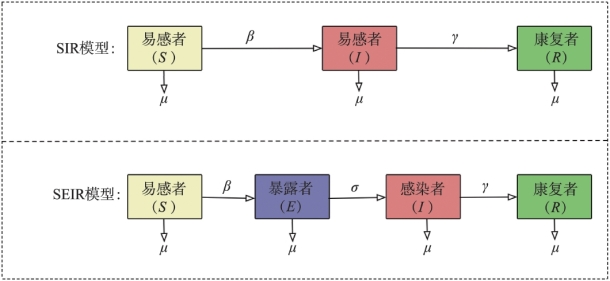
图5.14 SIR模型(上)和SEIR模型(下)各仓室人群流动图
每个感染者都具有传染力，当他们与易感人群接触时，就有可能将疾病传染给易感者，接触率与总人口数成正比。假设感染者个体和其他所有个体独立且随机分布，当人口总数量很大时，每个感染者在单位时间内能够接触到的易感者数目是有限的。易感者一旦被感染则直接移入染病者仓室(即不考虑潜伏期)，并在感染者仓室中停留平均1/γ的时间。SIR模型可以用微分方程表示:
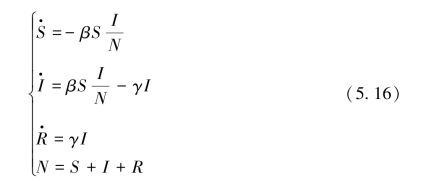
式中，N是人口总数；S是易感人群数；E是潜伏期人数；I是感染人数；R是康复人数；μ是死亡人数；β是易感人群的感染概率；γ是治愈率；I/N是S与I的有效接触率。
在传染病的动力学建模中，传染率系数是一个十分重要的参数，分为标准传染率系数和双线性传染率系数。双线性传染率系数假定每个感染者在单位时间内感染的易感者数目与研究环境中的总人口数成正比(夏智强，2016)，标准传染率系数假定每个感染者在单位时间内感染的易感者数目是一个固定值。在研究范围较大，总人口较多的情况下，采用标准传染率系数更加准确可靠。新冠肺炎以及一些季节性流感，染病者在染病初期并不会表现出症状，这段时间称为潜伏期，增加暴露者人群(exposed)的动力学模型为SEIR模型，人群各仓室之间的移动如图5.14所示，计算公式为:
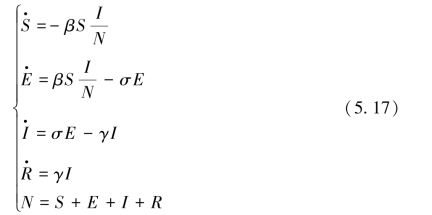
式中，E是暴露者人数；σ是潜伏期患者转化为感染者的比率。
通过起始值、时间值等参数设置，根据SIR模型的假设和反映移动规律的微分方程，可以模拟出在一段时间内各个仓室人群的人口变化规律。计算伪代码如算法5.1所示:
算法5.1 SIR模型
有关应急大数据的空间分析与多因素关联挖掘的文章
- 详细阅读
-
典型扩散连接设备及其工作原理详解详细阅读
表2-3-10是WorkhorseⅡ型和Centorr6—1650—15T型真空扩散连接设备的主要性能指标。图2-3-63 感应加热扩散焊机原理示意图图2-3-64 感应加热扩散连接设备3.超塑成形-扩散连接设备此类设备是由压力机和专用加热炉组成，可分为两大类。超塑成形-扩散用模具及工件置于两陶瓷平台之间，可以将待连接零件密封在真空容器内进行加热。高压氩气经气体调压阀，向装有工件的模腔内或袋式毛坯内供气，以获得均匀可调的扩散连接压力和超塑成形压力。......
2023-06-26
- 详细阅读
-
实验模型及方法详解详细阅读
实验采用对称的双断口结构，图6-25所示为实验模型的平面图及相关几何尺寸，单位均为mm。图6-25 气动斥力实验模型的平面图图6-26 气动斥力测试方法的原理图测量方法的原理如图6-26所示。下面的实验均是采用该方法进行的。图6-29 s=2mm，Im=4.2kA时的实验波形及电动斥力、气动斥力随时间的......
2023-06-15
- 详细阅读
-
Frame-Splitter模型实现详解详细阅读
拆分窗口类，可以将框架窗口分隔为上下或左右多个子窗口。1）在程序向导第1个步骤中，去掉“Document/View architecture support”选项，如图12-16所示。8）在主框架类CMainFrame类的头文件中，添加一些成员变量并去掉原有的CChildView类变量。9）在CMainFrame类的源文件中，去除m_wndView相关的代码。10）在CMainFrame类中，添加OnCreateClient虚函数并修改函数代码。图12-19 查看运行结果12）在CLeftView类中添加OnInitialUpdate虚函数，并修改代码初始化树形视图。①在框架类的虚函数OnCreateClient回调时，调用CSplitterWnd：：CreateStatic创建多行多列的分隔器。......
2023-11-25
-
PWM控制原理详解详细阅读
PWM 控制的理论基础是面积等效原理，即冲量相等而形状不同的窄脉冲加在具有惯性的环节上时，其效果基本相同。对于正弦波的负半周，也可以用同样的方法得到PWM 波形。像这种脉冲宽度按正弦规律变化而和正弦波等效的PWM 波形，称为SPWM 波形。图6.2冲量相等的各种窄脉冲的响应波形图6.3用PWM 波代替正弦半波要改变等效输出正弦波的幅值时，只要按照统一比例系数改变上述各脉冲的宽度即可。......
2023-06-23
-
电饭煲的工作原理详解详细阅读
当加热盘开始加热时，微处理器将显示信号输入到显示部分，以显示电饭煲当前的工作状态。指示灯由微处理器控制，根据当前电饭煲的工作状态，进行相应的指示。......
2023-06-26
相关推荐