莫兰指数I用标准化统计量Z来检验n个区域是否存在空间自相关关系，当Z值为正且显著时，表明存在正的空间自相关；当Z值为负且显著时，表明存在负的空间自相关，相似的观测值趋于分散分布；当Z值为零时，观测值呈独立随机分布。交通事故发生率的莫兰指数I为0.28，G观测值为0.001126，表明交通事故发生率具有强烈的空间相关性、聚集性，即某地的交通事故与该地区的位置有关。图3.21局部莫兰指数......
2023-06-15
全局自相关分析方法探讨
【摘要】：全局莫兰指数I是评价全局自相关性最常用的指标。全局莫兰指数I需要进行零假设检验，首先假定研究对象不存在空间相关性，然后通过Z得分检验来验证假设是否成立。表5.2全局自相关分析结果图5.9是2020年新冠肺炎确诊病例率全局自相关莫兰散点图，每个点代表了一个街区的集聚类型，第一象限为高-高集聚区，第二象限为低-高聚集区，第三象限为低-低集聚区，第四象限为高-低集聚区。
全局莫兰指数I是评价全局自相关性最常用的指标。其计算公式如下:
莫兰指数I的取值范围为(－1，1)，如果值为正表示空间对象的属性值的分布具有正相关性，负值表示该空间对象的属性值分布具有负相关性，0则表示空间对象的属性值不存在空间相关，即空间随机分布。
全局莫兰指数I需要进行零假设检验，首先假定研究对象不存在空间相关性，然后通过Z得分检验来验证假设是否成立。Z得分可以由莫兰指数I系数及其期望值和方差计算得到:
在零假设条件下(即不存在空间相关性)，期望值为:
当n趋于无穷大时，期望值为0。莫兰指数I的方差有两个假设:空间对象属性取值的正态分布假设和空间对象随机分布假设。当为正态分布时，方差为:
一般情况下，当｜Z｜＞1.96时，拒绝零假设，即在95%的概率下认为存在着空间自相关性。
以2020年12月下半月至2021年3月上半月这一时间段美国纽约市177个街区的新冠肺炎发病率数据为数据源进行全局自相关分析，每半个月为一个时间周期，分析结果见表5.2。从表5.2可以看出，莫兰指数I的值均大于0，且｜Z｜＞1.96，说明发病率数据呈现出明显集聚特征，P值为0.001，则说明这组数据随机生成的概率很小。莫兰指数I指数值范围在0.7439～0.79525之间，表示纽约街区的新冠肺炎发病率存在正向的自相关关系。
表5.2 全局自相关分析结果
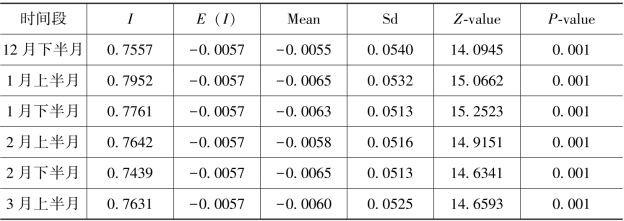
图5.9是2020年新冠肺炎确诊病例率全局自相关莫兰散点图，每个点代表了一个街区的集聚类型，第一象限为高-高集聚区，第二象限为低-高聚集区，第三象限为低-低集聚区，第四象限为高-低集聚区。大部分点位于一、三象限，斜率为正，表示正的空间自相关性。
图5.9 莫兰指数I散点图
有关应急大数据的空间分析与多因素关联挖掘的文章
- 详细阅读
-
自化之道：无为而民自化，探讨成才的格言详细阅读
一个人的求学、求知以致成长、成才，可看作是一个自身与所处环境发生实质性变化的过程。其中“我无为而民自化”，这是体现老子无为变化思想的名句，也是启发我们探讨成才之道的格言。简言之，我们称之为“自化之道”。......
2023-08-14
-
分层法的应用及分析方法探讨详细阅读
分层法又叫分类法，是将调查收集的原始数据，根据不同的目的和要求，按某一性质进行分组、整理的分析方法。现举例说明分层法的应用。钢筋焊接质量的调查分析，共检查了50 个焊接点，其中不合格19 个，不合格率为38%，存在严重的质量问题，试用分层法分析质量问题的原因。分层法是质量控制统计分析方法中最基本的一种方法，其他统计方法一般都要与分层法配合使用，如排列图法、直方图法、控制图法、相关图法等。......
2023-11-19
-
探讨中国奇迹：解析与相关问题详细阅读
对于中国经济增长的奇迹，钱颖一等的解释特别关注于制度安排。双轨制这一制度在价格、区域发展和不同所有制部门发展中的贯彻，可以看作解除管制逐步实现的明证，这些都有利于经济的平稳过渡。此外，体制外经济增量对一些国有企业的最终产品部门也形成竞争压力，硬化其预算约束，缓解其内在的激励问题。......
2023-12-02
-
关于变量相关关系的探讨与分析详细阅读
以两个变量为例进行讨论。这种关系x与y的关系点杂乱无章，如图X3.15所示。相关关系，指两个变量x与y之间的关系介于完全相关和零相关之，这种关系x与y的关系点呈带状分布趋势，如图X3.16所示。图X3.15零相关示意图图X3.16相关关系示意图直线相关；曲线相关例如，流域年径流深与年降水量之间的关系，就是相关关系。......
2023-06-21
-
基于贝叶斯网络的相关分析方法优化详细阅读
贝叶斯网络是基于概率分析和图论对不确定性知识进行表示的推理模型，它是一种模拟人类推理过程中因果关系的不确定性处理模型。贝叶斯分类器是用于分类的贝叶斯网络，它是各种分类器中分类错误概率最小或者在预先给定代价的情况下平均风险最小的分类器。通过对纽约市曼哈顿区2014年至2017年的交通事故数据构造朴素贝叶斯网络，对事故中伤亡人数进行分析。图4.1相关性分析结果......
2023-06-15
-
基于距离的全局特异数据挖掘概念和方法探讨详细阅读
Zhong Ning等人提出了一种基于距离的全局特异数据挖掘的构架[101]。其中，Mj和σj分别代表aj所有PF值的均值和标准差。Pr=RPF均值+γ×RPF的标准差（3.4）可以看出，此构架是基于距离的，并且找到的特异数据是全局的。从式（3.1）得出，属性xij和xkj间的距离d是后续计算的基础。由前述可知，此构架可以处理各类属性值，并且可以处理多个相关数据集的特异挖掘问题。......
2023-06-16
-
线性相关性分析方法简介详细阅读
相关性分析可以分为线性相关分析、偏相关分析、距离分析等。对交通事故与相关要素之间相关性进行计算时，由于数据不符合正态分布，所以选择Kendall相关系数、Spearman相关系数分析计算，得到Kendall及Spearman相关系数分析结果见表4.3，依次表示事故伤亡等级、日夜、季节、假期、风速、温度、天气、酒精、车速、大型车辆之间的相关系数和显著性。表4.3Kendall及Spearman相关系数分析结果......
2023-06-15
相关推荐