另外,随机森林法可以评价各种指标的重要程度。装袋算法通过自助抽样法有效地提高了随机森林算法的准确度。Breiman在1984年提出的分类回归树是一种不稳定的学习算法,因此CART方法与装袋算法结合就形成了随机森林算法,可以提高模型预测准确率。随机森林模型中某一特征的重要性,是所有决策树得到的该特征重要性的平均值。......
2023-06-15
交通事故影响因素涉及环境、人、车等因素,结合数据收集与文献查阅等方法,筛选了相关性较高的自变量作为预测交通事故的主要指标,见表4.12。
表4.12 影响指标

续表

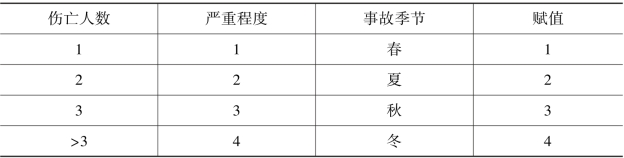
对于本研究数据,需要进行数量化处理,其中“是否在白天”、“是否在假期”是布尔型变量,直接赋值0和1即可。对于其他本研究变量,依次编码数值。把事故严重程度作为因变量进行训练和预测,事故的严重程度是根据伤亡人数来确定的,见表4.13,其他数据同理。
表4.13 数据量化示例
本研究共统计了5618起交通事故样本,随机选取全部样本的80%作为训练样本,20%作为测试样本。随机森林模型中有两类需要调整的参数,两类参数分别来自装袋算法框架和分类回归树。
装袋算法框架有两个重要参数:①最大决策树个数,最大决策树个数太小或太大,可能会导致模型的欠拟合或过拟合,而且当该参数大到一定程度时,对模型的提升不会有明显的帮助。因此我们需要寻找一个合适的值,一般情况下默认是100;②袋外分数,袋外分数是随机森林模型泛化能力的直接体现,是评估一个模型好坏与否的重要标准。
分类回归树的参数主要用来控制决策树,防止决策树过拟合。决策树中最重要、对模型影响最大的4个参数:①决策树划分节点时考虑的最大特征个数,需要一个合适的值来控制决策树的生成速度和质量;②决策树允许的最大深度,在数据量和特征数较多的情况下决策树会很庞大,通过限制决策树的最大深度,可以减小决策树,防止过拟合;③内部节点再划分所需的最小样本数,该参数值限制了决策树内部节点继续划分的条件,如果某个节点的样本数量小于这个值,则该节点处不会再选择最佳特征来进行划分;④叶子节点处含有的最小样本数,如果叶子节点处的样本数小于这个值,则应剪掉该节点和它的兄弟节点。
建立模型时用调参的过程和结果:将最大决策树个数的索引范围设置为(10,200),当最大决策树个数取79时,准确率最高,为0.9982;将决策树划分节点时考虑的最大特征个数的索引范围设置为(1,10),当决策树划分节点时考虑的最大特征个数取4时,准确率最高,为0.9986;将决策树允许的最大深度的索引设置范围为(1,50),当决策树允许的最大深度取24时,准确率最高,为0.9984;将内部节点再划分所需的最小样本数的索引设置范围为(2,50),当内部节点再划分所需的最小样本数取2时,准确率最高,为0.9986;将叶子节点处含有的最小样本数的索引设置范围为(1,50),当叶子节点处含有的最小样本数取1时,准确率最高,为0.9986。
为了分析影响纽约交通事故的特征,输出特征重要性如图4.6所示,由此可知,风速、温度、事故原因、涉及车辆等指标对纽约交通事故的伤亡程度影响较大。

图4.6 随机森林模型指标权重
为了验证模型的预测性能和泛化性能,利用测试集进行预测,准确率为81.32%,测试集的拟合程度如图4.7所示。这意味着模型不仅对训练样本具有较好的拟合效果,对于测试集也具有较好的预测能力和泛化能力,由此验证了该模型在预测纽约市交通事故严重程度的可行性和有效性。
将全部样本代入模型,以此来预测纽约市的交通事故,准确率为96.16%,拟合效果如图4.8所示。
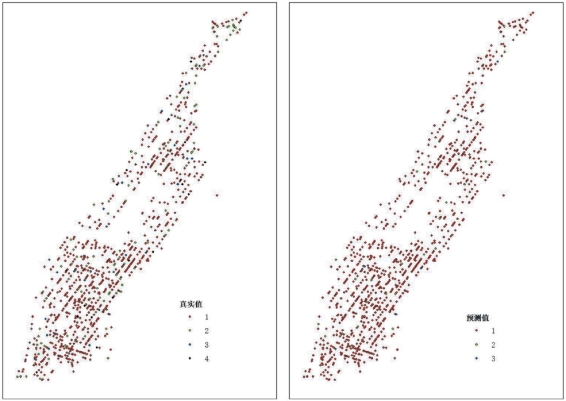
图4.7 测试样本真实值与预测值对比
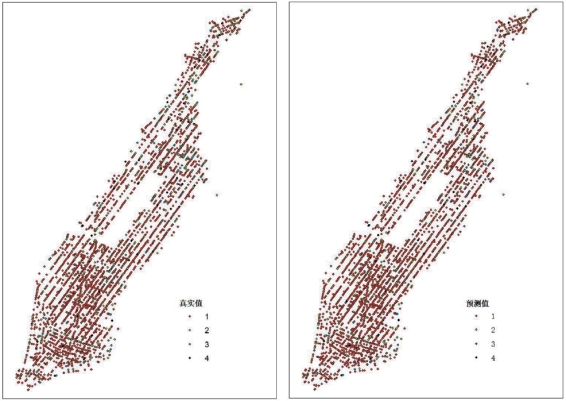
图4.8 全部样本真实值与预测值对比
有关应急大数据的空间分析与多因素关联挖掘的文章

另外,随机森林法可以评价各种指标的重要程度。装袋算法通过自助抽样法有效地提高了随机森林算法的准确度。Breiman在1984年提出的分类回归树是一种不稳定的学习算法,因此CART方法与装袋算法结合就形成了随机森林算法,可以提高模型预测准确率。随机森林模型中某一特征的重要性,是所有决策树得到的该特征重要性的平均值。......
2023-06-15

随机森林在运算量没有显著提高的前提下提高了预测精度。随机森林对多元共线性不敏感,结果对缺失数据和非平衡的数据比较稳健,可以很好地预测多达几千个解释变量的作用,被誉为当前最好的算法之一。随机森林是一个树型分类器的集合。随机森林在建立模型以及进行预测的具体步骤如图6-8所示。图6-8随机森林建模预测步骤①用N表示原始训练集样本的个数,用M表示变量的数目。这也是随机森林的一个非常重要的优点和特点。......
2023-06-28

电力负荷量会随着工业生产和气候的变化而变化,所以本书将数据按月份和日期类型来预测电力负荷。为了较充分地利用与电力负荷预测密切相关的天气语言信息,有必要引入模糊逻辑来确定预测日的电力负荷曲线形状。......
2023-08-25

本书在MATLAB语言平台编制五参数的随机车流模拟程序,该程序界面如图6.8所示。图6.8基于MATLAB语言的随机车流模拟软件图6.9随机车流模拟流程图在随机车流模拟软件的基础上,可方便快捷地实现随机车流模拟。图6.10随机车流统计数据与随机样本图车辆的日通行数量具有一定的波动性,但随着运营时间的增长总体呈上涨趋势。与多项式函数相比,指数函数与对数函数对预测车流模型有较好的效果。......
2023-09-19

描述工程结构中不确定性的基本方法就是随机变量与随机过程。随机变量的概率分析是描述随机变量概率特征的重要依据。简而言之,随机过程就是依赖于时间t的一主随机变量,则X称为随机过程在t1时刻的随机变量[15]。图1.2随机过程样本与均值的关系随机过程的方差D表示随机过程在t时刻对于均值点的偏离程度。仅对于正态随机过程而言,两者一致,工程中常用的是平稳随机过程。......
2023-09-19

回归模型分析预测法是根据事物内部因素变化因果关系来预测事物未来发展趋势。4)利用模型进行预测。图6-11 社会总产值预测值置信区域示意图6.3.3.2 多元线性回归预测法当预测对象Y受到多个因素X1、X2、…、Xm的影响,如果各个因素Xi与Y相关关系可以同时近似用函数关系来表示,则可以用多元线性回归预测模型进行预测。......
2023-07-15

计算结果从定性上与相应河段模型试验结果一致,定量上略有差别。小浪底水库调节后,出库沙量大幅度下降,特别是大于0.025m 的中、粗沙大部分被拦截在库区。......
2023-06-23
相关推荐