基于贝叶斯网络的相关分析方法优化

2025-09-29 历史故事版权反馈

【摘要】：贝叶斯网络是基于概率分析和图论对不确定性知识进行表示的推理模型，它是一种模拟人类推理过程中因果关系的不确定性处理模型。贝叶斯分类器是用于分类的贝叶斯网络，它是各种分类器中分类错误概率最小或者在预先给定代价的情况下平均风险最小的分类器。通过对纽约市曼哈顿区2014年至2017年的交通事故数据构造朴素贝叶斯网络，对事故中伤亡人数进行分析。图4.1相关性分析结果

贝叶斯网络(BN)是基于概率分析和图论对不确定性知识进行表示的推理模型(陈云，2015)，它是一种模拟人类推理过程中因果关系的不确定性处理模型。它是由节点和连接节点的有向边构成的有向无环图(DAG)，其中，节点表示可观察到的变量、隐变量、未知参数等随机变量；有向边表示的是节点之间的因果关系(父节点“因”指向子节点“果”)，节点之间因果关系强度用条件概率表示。

贝叶斯网络可以将决策相关的各种信息纳入网络结构中，按节点的方式统一进行处理，并用条件概率表达各个信息要素之间的相关关系，能在不完整、不确定的信息条件下进行学习和推理(陈坤，2013)。贝叶斯网络作为一种不确定性的因果关联模型，具有多元知识图解可视化形式，强大的不确定性问题处理能力以及多源信息表达和融合能力(曾华军，2003)，通过概率推理来实现事件发生的预测，在统计决策、专家系统和学习预测方面得到了较为广泛的应用。

贝叶斯分类器是用于分类的贝叶斯网络，它是各种分类器中分类错误概率最小或者在预先给定代价的情况下平均风险最小的分类器(李娜，2008)。其分类原理是通过某对象的先验概率，利用贝叶斯公式计算出其后验概率，即该对象属于某一类的概率，选择具有最大后验概率的类作为该对象所属的类。

贝叶斯决策论通过相关概率已知的情况下利用误判损失来选择最优的类别分类(宫明秀，2002)。将样本的类别记为c，样本的特性记为x，则“风险”(误判损失)就可以用原本为cj的样本误分类成ci产生的期望损失来衡量，期望损失可通过下式计算:

其中，λ是误分类所导致的损失。为了最小化总体风险，只需在每个样本上选择能够使条件风险R(c｜x)最小的类别标记。

朴素贝叶斯分类器是贝叶斯分类器中最简单，也是最常见的一种分类方法。朴素贝叶斯算法是有监督的学习算法，解决的是分类问题。基于属性条件独立性假设，后验概率P(c｜x)的估计公式为:(https://www.chuimin.cn)

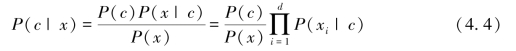
pagenumber_ebook=90,pagenumber_book=83

式中，d为属性数目；xi为x在第i个属性上的取值；P(c)是类“先验”概率，P(x｜c)是样本x相对于类标记c的类条件概率；P(x)是用于归一化的“证据”因子，对于给定样本x，证据因子P(x)与类标记无关。于是，估计P(c｜x)的问题变为基于训练数据来估计P(c)和P(x｜c)。P(c)可通过各类样本出现的频率来进行估计。

通过对纽约市曼哈顿区2025年至2025年的交通事故数据构造朴素贝叶斯网络，对事故中伤亡人数进行分析。数据集内容包括伤亡人数、季节、工作/休息日、节假日、天气、时间段、风速、气温、邮政区、事故因素、事故车是否是大型车辆、事故车车辆类型1及事故车车辆类型2等数据属性。数据集中5500条数据用于训练，525条数据用于验证。

计算结果如图4.1所示。根据结果显示，该地区的交通事故的伤亡人数主要与天气、时间段、工作/休息日、气温、事故因素类型、事故车辆是否是大型车辆、事故车辆类型等因素有关。同时，事故因素类型、事故车辆类型与时间段、天气等又存在内在联系。

在验证数据集中，有525条验证数据，411条数据得到正确分类，在95%的置信区间内，分类正确率为78.29%±3.53%。

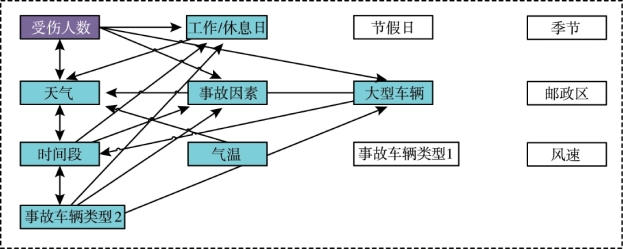
pagenumber_ebook=91,pagenumber_book=84

图4.1　相关性分析结果

基于贝叶斯网络的相关分析方法优化

相关推荐