，σ（αn）是线性无关的.因此，n≤m.综合上面的结论可以得到n=m，即V1，V2有相同的维数.充分性.设V1，V2都是n维线性空间，下面我们来建立一个从V1到V2的同构映射，从而证明V1V2.分别取V1的一组基α1，α2，…，αn之下的坐标是唯一确定的，而向量组β1，β2，…......
2023-11-22
线性相关性分析方法简介
【摘要】：相关性分析可以分为线性相关分析、偏相关分析、距离分析等。对交通事故与相关要素之间相关性进行计算时，由于数据不符合正态分布，所以选择Kendall相关系数、Spearman相关系数分析计算，得到Kendall及Spearman相关系数分析结果见表4.3，依次表示事故伤亡等级、日夜、季节、假期、风速、温度、天气、酒精、车速、大型车辆之间的相关系数和显著性。表4.3Kendall及Spearman相关系数分析结果
相关性分析是研究现象之间是否存在某种依存关系，并对具体有依存关系的现象探讨其相关方向以及相关程度(孙逸敏，2007)。相关性分析可以分为线性相关分析、偏相关分析、距离分析等。
说明两个样本量为n的变量(x，y)间关系密切程度的统计指标叫相关系数，用r表示。计算线性相关系数的基本公式如下:
有三种相关系数:Pearson相关系数、Spearman相关系数、Kendall相关系数。Pearson相关系数，是对定距连续变量数据进行计算；Spearman相关系数、Kendall相关系数，当分类变量的数据或变量值的分布明显非正态或分布不明时，计算时先对离散数据进行排序或对定距变量值求秩。
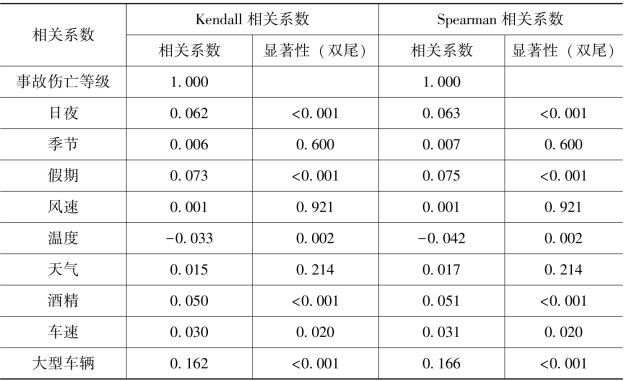
对交通事故与相关要素之间相关性进行计算时，由于数据不符合正态分布，所以选择Kendall相关系数、Spearman相关系数分析计算，得到Kendall及Spearman相关系数分析结果见表4.3，依次表示事故伤亡等级、日夜、季节、假期、风速、温度、天气、酒精、车速、大型车辆之间的相关系数和显著性。
结果显示，交通事故与日夜、假期、温度、酒精、车速、大型车辆的影响是显著相关的。
表4.3 Kendall及Spearman相关系数分析结果
有关应急大数据的空间分析与多因素关联挖掘的文章
- 详细阅读
-
敏感度分析方法简介详细阅读
然而，在不确定性情况下，这种方式就较难实现敏感度分析。因此，相关研究引入了许多解决不确定问题的方法，最常用的是蒙特卡洛模拟，并引进了等级相关系数来进行敏感度分析。因此，敏感度分析已经被广泛应用于各个领域，尤其在投资项目经济效益评估中使用较多。通过对已设置不同的概率分布函数的输入变量，进行多次独立的蒙特卡洛抽样，从而获得相应的预测变量值，用于随后的敏感度分析。......
2023-06-20
-
张宇线性代数9讲：判断相关性的7大定理详细阅读
，αn（n≥2）线性相关，则存在n 个不全为零的数k1，k2，…，αn 线性表示的表示法唯一.定理3 如果向量组β1，β2，…，αn 线性相关有非零解.仿定理4的研究方法，便有下面所给的定理5.定理5 向量β可由向量组α1，α2，…，αm 线性无关，则其任一部分向量组也线性无关.总之，向量组部分线性相关，则整体也线性相关；整体线性无关，则任一部分也线性无关.定理7 如果一组n维向量α1，α2，…......
2023-11-21
-
SERS技术简介：基于表面增强拉曼散射的分析详细阅读
通常认为信号增强是由两个基本机制解释的，即化学机制和电磁机制。CM是一种短距离效应，与表面吸附的分子和基材表面之间的电荷转移有关。与之对应的是，EM是一种远距离效应，源于增强的电磁场，通常能够提供比CM高得多的信号增强。与主要依靠LSPR诱导的EM的金属基板不同，非金属的信号增强来自分别对应于EM或CM的结构共振或电荷转移共振。......
2023-06-30
-
《左传》文学研究：线性和非线性叙述比较详细阅读
[2]这段来自西方叙事学的话语其实已经跨越了东西方的文化界限，而从本质上揭示了叙事过程中点、线、面的关系，也就是线性时间和非线性叙述的关系。正如前面所说的，时间对古代中国有着特别重要的指示意义，没有了线性时间，农事和以农事为核心的绝大多数社会活动都将失去依据和参照。......
2023-11-30
-
非线性数学模型线性化方法详细阅读
在建立控制系统的数学模型时，常常会遇到非线性的问题。严格地说，实际物理元件或系统都是非线性的。这种线性化方法称为小偏差线性化方法。通过上述讨论，在非线性数学模型进行线性化时应注意以下几点。若非线性特性是不连续的，处处不能满足展开成为泰勒级数的条件，这时就不能进行线性化处理。这类非线性称为本质非线性，对于这类问题，要用非线性自动控制理论来解决。......
2023-06-28
-
线性代数讲义：求极大线性无关组及相关问题详细阅读
，αn.初等行变换不改变列向量组的线性相关性.求此极大线性无关组.①构造A＝［α1，α2，…并在此时将向量α＝［4，1，6，10］T用α1，α2，α3，α4 线性表示；p为何值时，该向量组线性相关？......
2023-11-21
-
空间自相关分析方法介绍详细阅读
莫兰指数I用标准化统计量Z来检验n个区域是否存在空间自相关关系，当Z值为正且显著时，表明存在正的空间自相关；当Z值为负且显著时，表明存在负的空间自相关，相似的观测值趋于分散分布；当Z值为零时，观测值呈独立随机分布。交通事故发生率的莫兰指数I为0.28，G观测值为0.001126，表明交通事故发生率具有强烈的空间相关性、聚集性，即某地的交通事故与该地区的位置有关。图3.21局部莫兰指数......
2023-06-15
相关推荐