主成分分析法(PCA)通过降维的数据处理技术，将多个存在一定关联度的指标简化成几个综合指标，即我们所说的主成分(张拯，2016)。每个主成分可以反映出原始变量中的大部分信息，另外每个主成分所包含的信息是不会存在叠加、重复情况的，因此在对多个变量进行分析研究的时候，主成分分析法不仅可以简化原本复杂、冗杂的数据信息，并且在一定程度上可以将复杂的问题进行简化性处理，使得通过主成分分析法获得的数据更加具有科学性，并且更为直观地反映出我们想看到的信息。
用方程表示多个变量(x1，x2，…，xn)转化成几个综合变量(主成分)(Z1，Z2，…，Zn)，各个主成分之间互不相关(王莺等，2014):
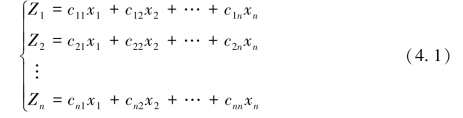
其中，x是原始变量X的标准化变量；cij(i，j＝1，2，…，n)为线性组合系数，叫做因子负荷量，它的大小以及正负号可以直接反映主成分与相应变量之间关系的密切程度和方向(王强等，2005)。
主成分分析法的主要优点包括:①可消除评估指标之间的相关影响。因为主成分分析法在对原始数据指标变量进行变换后形成了彼此相互独立的主成分，而且实践证明指标间相关程度越高，主成分分析效果越好。②可减少指标选择的工作量。对于其他评估方法，由于难以消除评估指标间的相关影响，所以选择指标时要花费较多精力，而主成分分析法可以消除这种相关影响，所以在指标选择上相对容易些。③主成分分析中各主成分是按方差大小依次排序的，在分析问题时，可以舍弃一部分主成分，只取前面方差较大的几个主成分来代表原变量，从而减少了计算工作量。用主成分分析法作综合评估时，由于选择的原则是累计贡献率≥85%，不至于因为节省了工作量却把关键指标漏掉而影响评估结果(杨勇等，2009)。
在计算时可以采用SPSS进行主成分分析，包括对描述、抽取、旋转、得分等参数设置后，便可以得到主成分分析报表，需要关注如下几个关键指标或报表:
(1)KMO和巴特利特检验
KMO检验根据变量间简单相关系数和偏相关系数的关系来检验变量数据。当所有变量的简单相关系数平方和远远大于偏相关系数平方和时，变量间的相关性越强，越适合进行主成分分析；反之，则不适合进行主成分分析。
巴特利特检验以原有变量的相关系数矩阵为出发点，其原假设是相关系数矩阵为单位矩阵，检验的统计量根据相关系数矩阵的行列式得到，根据自由度和统计量观测值查询卡方分布表，可近似得到相应的相伴概率值。根据相伴概率与显著性水平之间的关系来判定变量之间是否存在相关关系且适合主成分分析(解坤等，2017)。
对纽约交通事故进行主成分分析，从分析结果可以看出，KMO取样适宜性数量为0.491，巴特利特球形度检验的近似卡方值为1533.013，自由度为36，显著性小于0.001。
(2)总方差解释报表
总方差解释报表见表4.1，结果显示各个成分初始特征值中，有4个特征值大于1的成分，累计解释了原始指标53.085%的信息，略大于50%。
表4.1 总方差解释报表
(3)旋转成分矩阵
旋转成分矩阵结果见表4.2，表中第一列代表每个主题项的名称，一行代表一个主题项与每个提取因子的对应关系。在一般情况下，提取旋转成分矩阵中，因子载荷系数大于0.4的指标，作为对应主成分指标的构成指标，并根据指标构成对指标反映的维度进行概括。
结果显示:第一主成分由季节、温度组成，反映的是外界季节性的天气状况、温度等；第二主成分由假期、酒精组成，反映的是驾驶员自身的饮酒状态以及假期，社会人文因素影响；第三主成分主要由日夜、风速组成，反映的是每日光照、风力影响；第四主成分主要由车速以及大型车辆组成，反映的是车辆自身的条件状态对交通事故的影响。
表4.2 旋转后的成分矩阵
有关应急大数据的空间分析与多因素关联挖掘的文章
，xp 表示p 门课程，c1，c2，…＋cp xp．我们希望选择适当的权重能更好地区分学生的成绩．每个学生都对应一个这样的综合成绩，记为s1，s2，…，sn．如果这些值很分散，表明区分得好，就是说，需要寻找这样的加权，能使s1，s2，…，sn 尽可能的分散，下面来看它的统计定义．设X1，X2，…，Xp 表示以x1，x2，…，xp 为样本观测值的随机变量，如果能找到c1，c2，…，c1p）使得Var的值达到最大；（c21，c22，…，c3p）同时垂直于（c11，c12，…......
2023-11-18
为了说明什么是数据的主成分，先从数据降维说起。一般来讲，n维空间中的n个点一定能在一个n－1维子空间中分析。在上一段中，我们可以认为数据降维后并没有丢弃任何东西，因为这些数据在平面以外的第三个维度的分量都为0。主成分分析的思想:将n维特征映射到k维上(k＜n)，这k维是全新的正交特征。这k维特征称为主成分，是重新构造出来的k维特征，而不是简单地从n维特征中去除其余n－k维特征。......
2023-06-21
实际上主成分分析可以说是因子分析（factor analysis）的一个特例．主成分分析从原理上是寻找椭球的所有主轴．因此，原先有几个变量就有几个主成分．而因子分析是事先确定要找几个成分（component），也称为因子（factor）（从数学模型本身来说是事先确定因子个数，但统计软件是事先确定因子个数，或者把符合某些标准的因子都选入）．变量和因子个数的不一致使得不仅在数学模型上，而且在计算方法上......
2023-11-18
2009年14个首批沿海开放城市（大连市、秦皇岛市、天津市、烟台市、青岛市、连云港市、南通市、上海市、宁波市、温州市、福州市、广州市、湛江市、北海市）实现地区生产总值达到60 003．47亿元，全国国内生产总值为335 353．00亿元，首批沿海开放城市地区生产总值占全国的17．9%，大大高出了人口占全国的比重（7．1%）．在遵循合理性、代表性、系统性、可比性、可操作性及可获得性的原则下，选取了能......
2023-11-18
USJudgeRatings数据集（R 自带），该数据集来自psych包，需加载以及调用psych包．（1）首先查看USJudgeRatings数据集的信息该数据集包含了律师对美国高等法院法官的评分，数据包含43个观测值，12个变量．12个变量如下：CONT：律师与法官的接触次数；INTG：法官正直程度；DMNR：风度；DILG：勤勉度；CFMG：案例流程管理水平；DECI：决策效率；PREP：审......
2023-11-18
主成分分析也称主分量分析，旨在利用降维的思想，把多指标转化为少数几个综合指标。当然，这种情况也可以使用因子分析做到，所以它们的区分不是绝对的。可以说，因子分析是主成分分析的推广，也是一种把多个变量化为少数几个综合变量的多变量分析方法，其目的是用有限个不可观测的隐变量来解释原始变量之间的相关关系。因子分析主要用于：减少分析变量个数；通过对变量间相关关系探测，将原始变量进行分类。......
2023-08-23
那就是这些被选的主成分所代表的主轴的长度之和占了主轴长度总和的大部分．有些文献建议，所选的主轴总长度占所有主轴长度之和的大约80%即可．其实，这只是一个大体的说法；具体选几个，要看实际情况而定．但如果所有涉及的变量都不那么相关，就很难降维．不相关的变量就只有自己代表自己了．......
2023-11-18
对4 种植物不同器官的生物量、δ13C 值组成及N、P、K 营养元素含量进行主成分分析，结果如表6-5 所示，最终得到3 个特征值大于1的主成分，累计百分比为78.95%，可以反映原始指标的大部分信息。表6-5不同主成分的特征值和累积贡献值 Table 6-5Principal component variance analysis表6-6主成分载荷矩阵 Table 6-6Principal Component Load Matrix图6-5干旱胁迫对4 种植物生物量、δ13C 值及营养元素影响的主成分分析 Fig.6-5The principal component analysis of the effects of drought stress on biomass， δ 13C value and nutrient elements of 4 plant species......
2023-11-04
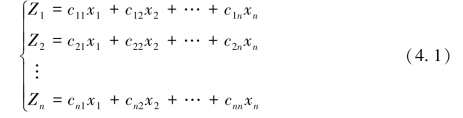
相关推荐