全局莫兰指数I是评价全局自相关性最常用的指标。全局莫兰指数I需要进行零假设检验，首先假定研究对象不存在空间相关性，然后通过Z得分检验来验证假设是否成立。表5.2全局自相关分析结果图5.9是2020年新冠肺炎确诊病例率全局自相关莫兰散点图，每个点代表了一个街区的集聚类型，第一象限为高-高集聚区，第二象限为低-高聚集区，第三象限为低-低集聚区，第四象限为高-低集聚区。......
2023-06-15
空间自相关分析方法介绍
【摘要】：莫兰指数I用标准化统计量Z来检验n个区域是否存在空间自相关关系，当Z值为正且显著时，表明存在正的空间自相关；当Z值为负且显著时，表明存在负的空间自相关，相似的观测值趋于分散分布；当Z值为零时，观测值呈独立随机分布。交通事故发生率的莫兰指数I为0.28，G观测值为0.001126，表明交通事故发生率具有强烈的空间相关性、聚集性，即某地的交通事故与该地区的位置有关。图3.21局部莫兰指数
空间自相关反映的是一个区域单元上的某种地理现象或某一属性值与邻近区域单元上同一现象或属性值的相关程度，是一种检测与量化从多个区域单元取样值变异的空间依赖性的空间统计方法(刘爱利，2012)。空间自相关理论认为彼此之间距离越近的事物越相像。当某一测样点的属性值高，而其相邻点同一属性值也高，称为正相关；反之称为负相关(刘渤海，2019)。当空间自相关仅与两点间距离有关，称为各向同性；当考虑方向的影响时，可能在不同方向上属性值与距离的关系不同时，称为各向异性。
空间自相关性使用全局和局部两种指标。全局指标用于探测整个研究区域的空间模式，使用单一的值来反映该区域的自相关程度。局部指标计算每一个空间单元与邻近单元就某一属性的相关程度。莫兰指数(Moran's I)和Geary系数就是两个用来度量空间自相关的全局指标。莫兰指数反映的是空间邻接或空间邻近的区域单元属性值的相似程度，Geary系数与莫兰指数存在负相关关系。
对于位置的观测值，该变量的全局莫兰指数I，用如下公式计算(温惠英，2008):
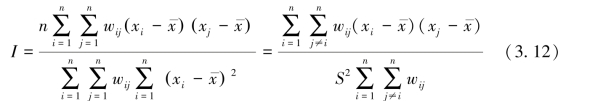
空间关联局部莫兰指数计算公式如下:
统计量Z的得分计算公式如下:
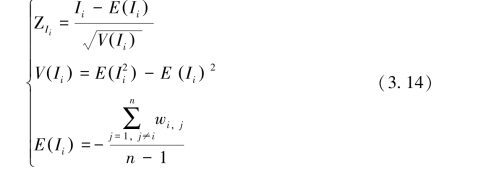
当Ii的取值为正值时，说明具有同样高或同样低的加权邻近采样；当Ii的取值为负值时，说明不具有同样高或同样低的加权邻近时空采样。
莫兰指数I用标准化统计量Z来检验n个区域是否存在空间自相关关系，当Z值为正且显著时，表明存在正的空间自相关；当Z值为负且显著时，表明存在负的空间自相关，相似的观测值趋于分散分布；当Z值为零时，观测值呈独立随机分布。
以纽约市2020年交通事故的数据为例，其作为国际化大都市，不仅拥有地铁、汽车客运站、火车站、飞机场等一批重要的交通枢纽，而且其境内道路网络纵横交错，交通情况较为复杂。对交通事故数据进行全局指标的空间自回归，得到莫兰指数和Geary系数的计算结果见表3.7。交通事故发生率的莫兰指数I为0.28，G观测值为0.001126，表明交通事故发生率具有强烈的空间相关性、聚集性，即某地的交通事故与该地区的位置有关。Z得分约为158，表明是标准差的158倍，结果分布在正态分布的两端，结合莫兰指数为正，可以得出结果分布在正态分布的右端，为聚集型。
表3.7 交通事故的空间自相关计算结果
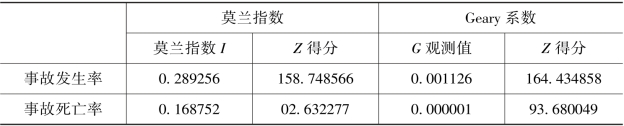
计算结果表明，交通事故发生率、死亡率具有强烈的空间相关性、聚集性，在具有较多车道数和较大宽度的城市主干道上，交通流量较大；同时，较大的交通流量又很容易导致拥堵状态，从而更容易引发交通事故。而支路、郊区路段车流量少，发生的交通事故数相对较少。但由于车速快，一旦出现交通事故，更容易导致伤亡事件发生。
局部莫兰指数的空间自回归计算结果如图3.21所示。从局部相关的角度来看，高值(HH)聚类、低值(LL)聚类的点明显多于HL、LH的点，即表示“低-低”型和“高-高”型聚集的区域较“高-低”型、“低-高”型的区域更多。结果说明，发生交通事故数较低(高)的区域在空间上更易聚集。从差异的角度来看，若“低-低”型和“高-高”型区县数量多，即说明此时的空间差异较小。
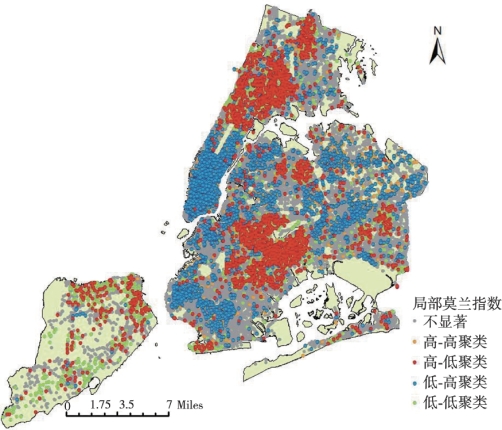
图3.21 局部莫兰指数
有关应急大数据的空间分析与多因素关联挖掘的文章
- 详细阅读
-
一维信号分析方法介绍详细阅读
图7-1 抽取器和内插器yD=x （7-1）即信号通过抽取器后，只有在M的整数倍时刻点被保留下来。式（7-3）说明，内插后的信号带宽压缩为原来的1/L，周期为2π/L。式（7-8）表明，抽取后的频谱等于原信号频谱膨胀M倍后再分别平移2kπ得到的M个谱之和，幅度则为原来的1/M。图7-8 一维信号抽取和内插实验图7-8 一维信号抽取和内插实验......
2023-06-23
-
电压空间矢量技术介绍详细阅读
2）在开关状态SASBSC=110时，即K1、K3、K2接通，，，将uA、uB、uC代入式（5.1）得图5.2 三相逆变器电压空间矢量式（5.4）表明，逆变器开关状态为110时uS2的幅值为2，方向为。依次类推，可得逆变器六种开关工作状态下的电压空间矢量uS1～uS6，电压空间矢量uS1～uS6的幅值相同，方向依次相隔60°，如图5.2所示。开关状态000和111，即下桥臂开关K4、K6、K2或上桥臂开关K1、K3、K5同时导通，空间电压矢量uS7=uS8=0，在坐标原点。......
2023-06-19
-
空间相关性分析：方法与应用详细阅读
图6.25入室盗窃犯罪数量分时间分区域统计图为探明哪些社会经济指标对抗议事件的发生有影响，哪些指标的影响是正面的，哪些指标的影响是负面的，本研究使用了栅格数据相关性分析方法。图6.27栅格相关性分析矩阵由于相关矩阵的对称性，可以用三角矩阵的形式描述相关性。......
2023-06-15
-
应急大数据的空间分析方法详细阅读
应急大数据的时空分析从地理空间位置和时间的角度分析了突发事件的演变情况，按照时间尺度的长短可以分为长期发生规律和短期内突发事件发展过程研究；根据空间范围的大小则可以分为大、中、小尺度的分布特性、发展趋势研究。国内发表的论文主要研究内容包括灾害时空变化、空间格局和影响因素。......
2023-06-15
-
涂层评价体系相关因素介绍详细阅读
同样的喷涂材料，选用不同的喷涂方法，其涂层性能，如结合强度、硬度、孔隙率等有明显的差别。3）涂层性能与试样制备有关。进行抗拉强度试验时，涂层表面的平整性和对偶件表面的表面粗糙度都会影响检测结果。由于涂层组织中的硬质相与基体结合力较低时，取样抛光不当，就可能发生硬质相脱落，而误判为涂层孔隙。由于上述原因，给热喷涂涂层性能评价带来很大难度。......
2023-06-18
-
图书馆财务分析方法的分析介绍详细阅读
财务分析是根据有关信息资料，运用特定方法，对图书馆财务活动过程及其结果进行总结和评价的一项工作。图书馆财务分析过程一般包括如下几个阶段：确定题目，明确目标。即把某些彼此相关联的指标以比率的形式加以对比，据以确定图书馆经济活动变动程度，揭示图书馆财务状况的一种分析方法。通过动态比率，可分析图书馆财务活动及相关指标的发展方向及增减速度。......
2023-07-25
-
目标的向量空间表示模型方案介绍详细阅读
一个目标在上述约定下可以看成是n维空间中的一个向量，这就是向量空间模型的由来。下面结合目标的表示，给出其定义。，td}；2）依据目标特征项序列，对训练集和测试集中的各个目标样本进行权重赋值、规范化等处理，将其转化为机器学习算法所需的模式向量。图6-2 目标的向量空间模型示意图......
2023-06-28
相关推荐