由于不同的分段起点，可能存在N个不同的数据段都包含待插值的样点I，即将产生N个不同的插值结果，全相位插值就是取这N个插值的均值作为最终结果。正反变换定义如下：式中Walsh变换基只有±1离散值，傅里叶变换基有复数，因此选择DCT基作为插值的正交变换。图8-23 八点全相位DCT内插核时频图（N=5）对与上面实验中相同的Chirp信号进行插值重建，实验结果如图8-24所示。......
2023-06-23
克里金插值优化技巧与应用
【摘要】：同时，克里金插值能给出插值的误差，使插值的可靠程度一目了然。例如，对纽约市的交通事故数据进行克里金插值分析。最终得到的普通克里金插值结果如图3.20所示。从普通克里金插值结果中还能清晰地看出交通事故是沿城市的主要道路分布的。
克里金插值是利用区域化变量的原始数据和变异函数的结构特点，对未采样点的区域化变量的取值进行线性无偏最优估计的一种方法(冯锦霞，2007)。相对于普通变量，区域化变量具有随机性、结构性、空间局限性、不同程度的连续性和不同类型的各向异性的特点。
变异函数描述的是区域化变量空间变化特征和强度，被定义为区域化变量增量平方的数学期望。变异函数有自己的自变量、因变量和函数表达式(刘爱利，2012)，其因变量为步长(h)，自变量为变异值，计算公式为:
在数据网格化的过程中，克里金插值考虑了描述对象的空间相关性质，使插值结果更科学、更接近于实际情况。同时，克里金插值能给出插值的误差(克里金方差)，使插值的可靠程度一目了然。克里金插值的公式(翁敏，2019)如下:
式中，z∗(x0)是点(x0，y0)处的估计值；λi是权重系数。它同样是用空间上所有已知点的数据加权求和来估计未知点的值。但权重系数并非距离的倒数，而是能够满足点(x0，y0)处的估计值与真实值的差最小的一套最优系数。
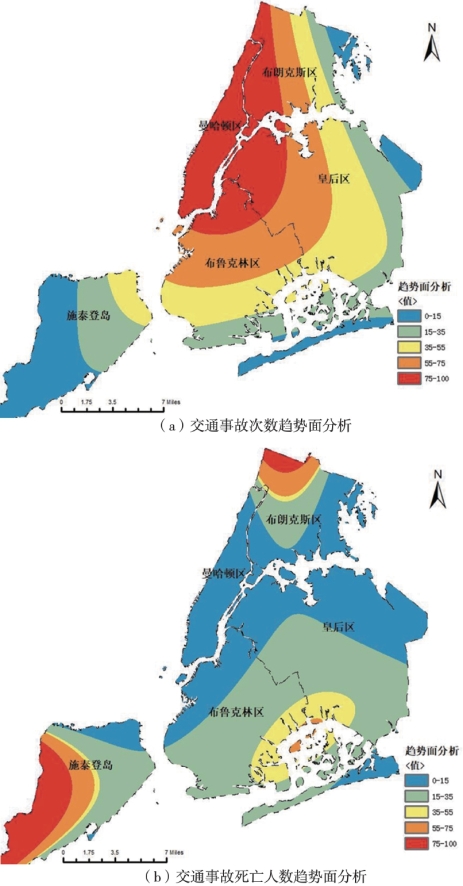
图3.18 纽约市交通事故次数和死亡人数趋势面分析
克里金插值可以分为6种类型:普通克里金插值满足本征假设，区域化变量的平均值是未知的常数；简单克里金插值满足二阶平稳假设，变量的平均值是已知的常数；泛克里金插值的变量的数学期望是未知的变化值，即样本非平稳；对数正态克里金插值则是在数据不服从正态分布时使用；指示克里金插值有真实的特异值，在需估计风险、概率分布时使用；协同克里金插值适合于相互关联的多元区域化变量(王艳妮，2008)。
例如，对纽约市的交通事故数据进行克里金插值分析。采用普通克里金插值的方法进行分析，首先创建半变异函数，半变异函数有球面函数、指数函数、高斯函数、线性函数等多种类型，所选模型会影响未知值的预测，尤其是当接近原点的曲线形状明显不同时，接近原点处的曲线越陡，最接近的相邻元素对预测的影响就越大，每个模型都用于更准确地拟合不同种类的现象。采用指数函数作为半变异函数，如图3.19所示，图(a)为指数函数拟合情况，图(b)为半变异图。
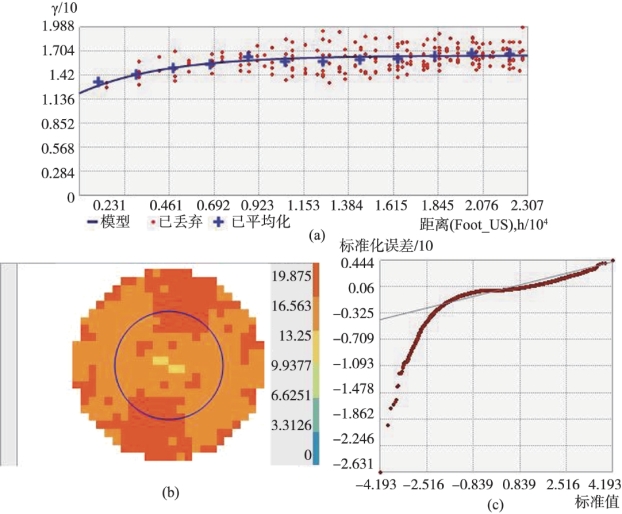
图3.19 指数函数、半变异图和内部检核精度结果图
创建经验半变异函数之后，根据点拟合模型，形成经验半变异函数。半变异函数建模和在回归分析中拟合最小二乘直线相似。拟合后变异函数的用途是确定局部内插需要的参数。用变异函数测定空间相关要素，如果不存在空间相关，那么变程很小；相反，较远距离的已知点之间的变异函数较大。图3.19(c)为内部检核精度结果。
最终得到的普通克里金插值结果如图3.20所示。可以看出，交通事故多发生在布朗克斯区、曼哈顿区和布鲁克林区的城市中心地带。从普通克里金插值结果中还能清晰地看出交通事故是沿城市的主要道路分布的。因此，对交通事故频发的路段，可以考虑通过添加道路辅路、合理设置交通信号灯等措施以改善交通状况。
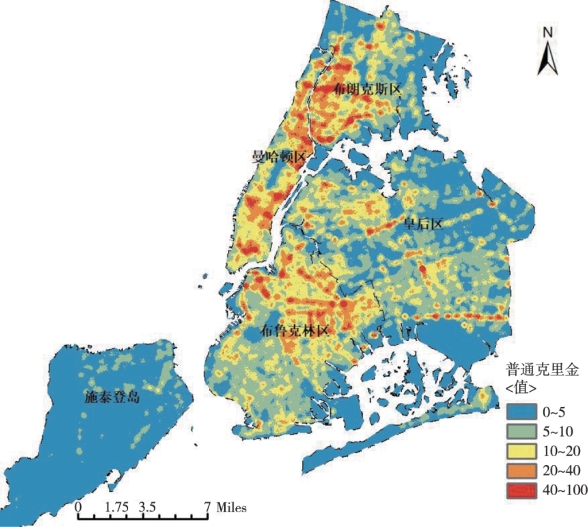
图3.20 普通克里金插值结果图
有关应急大数据的空间分析与多因素关联挖掘的文章
- 详细阅读
-
内插与外推VI多种插值方法解析详细阅读
内插与外推VI可以用于进行一维和二维插值、分段插值、多项式插值和傅里叶插值如图9-30所示。图9-31 一维插值 VI节点下面介绍各输入、输出端选项含义。如果xi输入端已连线，则该VI将忽略n次。将错误连接至“错误代码至错误簇转换”VI，可将错误代码或警告转换为错误簇。该VI可提供5种不同的插值方法。图9-32 “多项式插值 VI”节点图9-33 “样条插值VI”节点在区间[xi,xi+1]，下列等式为输出插值y。......
2023-11-07
-
时空配准运动插值方法在虚拟现实应用中的实践详细阅读
我们研究基于时空配准的运动插值算法，解决人体运动的参数插值问题，包括时间配准、空间配准、帧插值和约束重建四个步骤。下面以两个运动M1、M2为例，介绍基于时空配准的运动插值算法。图5-13显示了采用贪心算法得到的配置曲线的效果图。严格来说，方位配准曲线与时间配准曲线完全不同，并非一条坐标系下的曲线，而是基于时间配准曲线的一系列数值。......
2023-10-17
-
克里金系统模型解析储层裂缝与多相流耦合详细阅读
为了考察裂缝尖端扩展动力学因素对裂缝属性随机分布的影响，我们在趋势克里金估计系统的基础上，建立多场趋势克里金系统模型，该模型将裂缝特征属性（）Z X的分布估计模型写作两项之和：其中 X是确定部分，也就是根据裂缝反演系统获得的裂缝分布趋势， X则是具有空间相关性的随机变量。根据公式，定义小尺度裂缝多场趋势克里金估计结果的方均根相对误差和绝对值相对误差。......
2023-08-20
-
UGNX10.0钣金概述及应用技巧详细阅读
图8.1.2 “钣金首选项”对话框（一）◆ 在区域中可以设置以下四个参数。图8.1.4 “钣金首选项”对话框（三）在“钣金首选项”对话框中单击选项卡，此时“钣金首选项”对话框（四）如图8.1.5所示。图8.1.6 “钣金首选项”对话框（五）......
2023-10-17
-
针通孔插装技术优化为：针孔插装技术简介详细阅读
正因如此，这种技术被称作针通孔插装技术。相较于表面贴装技术，这种针通孔插装技术具有更好的机械可靠性，但成本也更高。图1.6镀铜、浸锡后的通孔截面照片针通孔插装技术的潜在应用是用于硅片上大尺度通孔的镀覆。在1.4.3节倒装芯片技术中的热应力问题讨论后，这将会被明确提出。通孔的直径是10~100μm，这与倒装芯片的焊球尺寸接近。此时，当硅片和硅基板连接时，热应力会非常小甚至不存在。......
2023-06-20
-
方向控制插装阀的应用与优势详细阅读
图4-57 插装阀用作单向阀图4-58 插装阀用作液控单向阀2.插装阀用作换向阀每个插装单元都具有通、断两种状态，若将几个插装单元组合起来，用电磁换向阀作先导控制阀，便可组成m位n通插装式换向阀。供给电磁先导阀的控制液压油亦可以是独立的，如图4-59c所示，控制盖板的X口接外控油液，电磁先导阀换向则插装阀开启或关闭。图4-62 四位四通插装换向阀图4-63 十二位四通插装阀......
2023-06-15
-
桥涵水文学：资料插补与延长技巧详细阅读
采用水文统计法推算设计流量时，如果水文站的流量观测资料系列较短或有缺测年份，则应尽量利用上下游或邻近流域内的水文站观测资料，进行插补和延长。位于同一河流上、下游的两个水文站，若两站之间无较大支流汇入，而且两站已有的流量观测资料中，相同年份的年最大洪峰流量大致成比例关系，则可利用两站对应的年最大洪峰流量，绘制两站的流量关系曲线，进行插补和延长。若上游的两支流河道上均有水文站，可以作为参证站。......
2023-11-20
相关推荐