太极推手中的技击方法一般分击法、拿法、跌法,其中击法最为常用。传统太极推手以锻炼为主,如拳击、脚踢、顶肘、撞膝、撩阴、锁喉、拿穴等伤人的狠毒招式禁止使用。太极拳被称为哲学拳、文化拳、道德拳,不是主动去找人打斗,也不采取先下手为强去攻击别人,是在被动的情况下化而击之。太极的无敌便是不与人争斗,“不争而善胜,不召而自来”,引进落空,四两拨千斤。现在一般认为以控制关节为手段的技法统称为擒拿。......
2023-10-17
概率论与数理统计学的一个关键问题是通过已知的数据对原始数据的概率分布密度函数进行估计(Elvik R,1997),估计的方法通常有参数估计法与非参数估计法两大类。参数估计法是指假定已知事件数据的分布具有比如线性、可化线性或指数形态以及其他特定形态等特定的规律,然后对假定的特定模型中的待求参数进行求解。在参数估计中,对已知原始数据的总体分布规律作出的假设会严重影响参数估计的结果。而非参数估计方法仅仅通过已知事件数据的分布情况,完全根据事件数据本身的分布规律对事件在整个区域内的分布情况进行估计,因此越来越多地被应用于相关的研究中。
Parzen(1962)和Rosenblatt(1956)提出的核密度估计法(KDE)是非参数估计方法中一种重要的方法。核密度估计法的核心继承自直方图法,但是其分析精度和连续程度较直方图法更优,因此被广泛应用于犯罪、交通事故以及传染病等公共安全事件的热点分析中。
在核密度估计方法中,通过以某点为中心的一定范围内所包含的数据点来计算该中心点处的密度值,其基本原理如图3.8所示。在图3.8中,以区域内某一点S作为圆心,以宽窗h为半径,通过计算搜索半径范围之内的数据点对点S处的核密度估计值之和,进而得到点S处的核密度值大小。数据点对点S处的核密度的估计值大小是根据核函数K计算而确定的,事件点i对点S处的核密度估计值根据核函数的不同而随着其与点S之间距离的变化而变化。
点S处的核密度估计值的计算公式如下:


图3.8 欧氏距离和网络距离的对比
点i到点S的距离表示方法有很多种,在普通的核密度估计方法中使用的是欧氏距离法,但这种距离描述方法在交通事故的核密度估计中却不太适合,因为交通事故通常发生在城市道路上,故研究区域不是整个MN17区,而应该具体到MN17区的路网中。因此,应该对核密度估计法进行相应的改进。
如图3.8所示,在路网中,以点S为圆心,窗宽h为半径形成的圆形区域内的交通事故点均为欧氏距离下所包含的点;而以点S为起始点,窗宽h为网络距离阈值,所覆盖的道路网络的路段范围如图3.8中加粗直线所示,在此加粗线上的交通事故点为网络距离下所包含的点。图中,点S在欧氏距离下的核密度估计值受11个事故点影响,而在网络距离下受其中9个事故点影响。在对交通事故进行核密度估计时,采用网络距离代替欧氏距离能够更真实地体现点S处的核密度估计值。
采用网络距离的核密度估计首先对路网进行分割,形成长度相等的道路子路段,然后以道路子路段S为核中心,窗宽h为网络距离阈值,进而得到该子路段的核密度估计值,如图3.8所示。需要注意的是,只有在道路子路段S的网络距离阈值h范围内的事件点才会对道路子路段S处的密度估计值有影响。因此,路网中子路段S的网络核密度估计值计算公式如下(陈金林,2015):


由Knox时空交互检验的分析结果可知,交通事故在空间和时间上的分布都是聚集的,而网络核密度估计只考虑空间维度,没有涉及时间维度,因此,为找出交通事故在时间上的差异,需要对网络核密度估计进行时间维度的扩展。如图3.9所示,AB为路网中的一个子路段,对AB进行时间的拓展就可以构造出时空子路段(Romano B,et al,2017)。

图3.9 时空子路段
时空网络核密度估计法,是以时空子路段为核中心,以空间宽窗hS为网络距离阈值,以时间宽窗ht为时间间隔阈值,进而计算在时空网络距离阈值范围内的事件点对时空子路段的核密度估计值的贡献(王颖志等,2019)。时空子路段(S,t)的核密度估计值计算公式如下:

在所构建的加权时空网络核密度估计模型的基础上,对MN17区交通事故点进行识别。具体步骤如下:
(1)将路网分割成时空子路段
将经过处理的MN17区的城市道路网络划分成等距离的线性子路段,如图3.10所示,图中实线为路网,白色点为分割路网的点。划分的线性子路段长度通常为最佳空间窗宽的1/10,最佳窗宽计算公式为:
![]()
其中的σ以交通事故数据空间距离和时间间隔的标准差来替代。
图3.10 路网分割后的子路段
通过计算,可以得到最佳空间窗宽hs为117.2m,线性子路段的长度为11.72m。分割后可能存在不足11.72m的路段,也将其视为完整的线性子路段进行保留。通过划分,可以得到4821条线性子路段。同理,通过计算得到最佳时间窗宽ht为0.78h,取其1/10作为时空子路段的时间间隔,但是当时空子路段的时间间隔小于lh时,计算量会成倍地增加,而且对实际的参考价值不大。因此,将最佳时间窗宽ht定成3h,时空子路段的时间间隔定成1h,因此可以得到4821×24条时空子路段。
(2)找出子路段在宽窗范围内的所有事故点
分割好时空子路段之后,找出时空子路段时空宽窗范围内所有的交通事故点并存储,存储的属性见表3.7。
表3.7 时空子路段R0宽窗范围内事故点属性

(3)计算时空子路段节点的核密度估计值
得到每个时空子路段时空宽窗范围内所对应的所有事故点之后,计算每个时空子路段所对应的加权时空网络核密度值,其算法伪代码如算法3.1所示。
算法3.1 加权时空网络核密度估计算法伪代码

计算2015年至2018年MN17区各时空子路段的加权核密度估计值,即各子路段在一天中的24个时段的加权核密度估计值,对计算结果进行可视化,如图3.11所示。

图3.11 交通事故加权时空网络核密度估计
各个时空子路段的加权网络核密度估计值如图3.12所示。然后,选用合适的统计方法对核密度估计结果进行进一步的处理,进而识别出纽约市MN17区的交通事故黑点。
从图3.13中可以看出,80%的核密度估计值小于最大值的二分之一,仅有少部分的核密度估计值比较高。为定量地识别出交通事故黑点(频发和严重程度较高)路段,需要在上述分析结果的基础上采用科学可行的方法对交通事故黑点进行识别。

图3.12 交通事故网络核密度估计结果
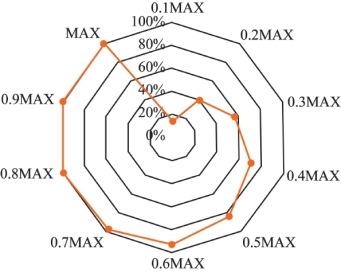
图3.13 子路段核密度估计值累计频率雷达图
有关应急大数据的空间分析与多因素关联挖掘的文章

太极推手中的技击方法一般分击法、拿法、跌法,其中击法最为常用。传统太极推手以锻炼为主,如拳击、脚踢、顶肘、撞膝、撩阴、锁喉、拿穴等伤人的狠毒招式禁止使用。太极拳被称为哲学拳、文化拳、道德拳,不是主动去找人打斗,也不采取先下手为强去攻击别人,是在被动的情况下化而击之。太极的无敌便是不与人争斗,“不争而善胜,不召而自来”,引进落空,四两拨千斤。现在一般认为以控制关节为手段的技法统称为擒拿。......
2023-10-17

底筋长度=板跨净长+伸入长度×2+2×弯钩底筋深入长度有以下几种情况:支座为混凝土梁、墙(图59)图58 板底筋长度翻样简图图59 支座为混凝土梁、墙注:hc为支座宽度。图512 板上部纵筋翻样简图a)端部为梁 b)端部为墙 c)柱上板带板上部纵筋支座内水平投影长度=la-a如果板制作宽度较大,远远大于时,板上部纵筋需要弯折。......
2023-08-26

解:L1=1/3边净跨长度+0.4laE=5000/3+14.8d≈mm≈2022mmL2=15d=15×24mm=360mm下料长度=L1+L2-外皮差值=2022+360-2.931d=mm≈2312mm3.边跨上部二排直角筋的加工、下料尺寸计算边跨上部二排直角筋的加工、下料尺寸和边跨上部一排直角筋的加工、下料尺寸的计算方法,基本相同。......
2023-08-26

它只是一棵极为普通、极其平常的树种,落叶乔木,叶子宽卵形,花单性,白或粉红色,果实圆形,成熟时黄红色,味道酸甜的杏子的杏树。而我家的甜核大杏,因味甜核香总是供不应求的。甜核杏树从利斧下救了下来,我用泥巴糊住了树干上那个深深的伤口,又用草绳缠裹结实,时间不长,它竟长合痊愈了。我家的甜核杏树是那次劫难中唯一的幸存者......
2023-08-09

图420 角柱顶筋计算角柱顶筋中的向边筋三、四排计算公式,如图422和图423所示。图421 角柱顶筋中的远梁筋二排计算注:钢筋用于焊接连接。......
2023-08-26

图331 中间跨下部筋的示意图下料长度L1=中间净跨长度+锚入左柱部分+锚入右柱部分锚入左柱部分、锚入右柱部分经取较大值后,各称为“左锚固值”“右锚固值”。请注意,当左、右两柱的宽度不一样时,两个“锚固值”是不相等的。具体计算见表321~表326。表324 HRB400级钢筋C30混凝土框架梁中间跨下部筋计算 表325 HRB400级钢筋C35混凝土框架梁中间跨下部筋计算 表326 HRB400级钢筋≥C40混凝土框架梁中间跨下部筋计算 解:参见表325。......
2023-08-26

效价单位是衡量抗生素有效成分的尺度,也是衡量抗生素性能的指标,其表示方法一般可以分成两类。质量单位以抗生素的有效成分的质量作为抗生素的单位,称为质量单位。某些抗生素的效价基准有特殊规定。一种抗生素有一个效价基准,同一种抗生素的各种盐类的效价可根据其相对分子质量与标准盐类进行换算而得。一般应根据医疗要求及生产技术水平,由中国药典作出有关规定,药厂生产的抗生素成品效价必须符合药典规定水平。......
2023-06-24
相关推荐