空间探索分析技巧

2023-06-15 历史故事版权反馈

【摘要】：图3.6MN17区交通事故的空间分布特征一组数据点在空间上的聚集性和方向性可以用标准差椭圆来描述。通过计算，得到MN17区交通事故点的平均最邻近距离为2.25 m，计算事故点之间的平均时间间隔为6.63小时。采用置信度为95%的统计显著性对结果进行判断，结果表明，MN17区的交通事故具有时空聚集性和显著的时空交互性，即交通事故在时间上也呈现出聚集模式。

以纽约市2015—2018年交通事故发生次数最多的曼哈顿区的MN17人口普查区为研究对象，利用平均中心和标准差椭圆进行交通事故空间分布模式分析，再通过Knox时空交互检验方法对交通事故是否呈时空聚集分布进行判断，分析出MN17区的交通事故具有时空聚集性和显著的时空交互性。

1.平均中心与标准差椭圆

一组事件点的平均中心是指对所有事件点的空间位置进行算术平均计算，可以根据一组事件点的平均中心发现该组事件点的空间集中位置和随时间偏移的规律(Mitchel A E，2005)，通过计算交通事故数据平均中心位置，可以直观地发现交通事故的聚集情况。通过不同时间下平均中心的位置偏移，可以挖掘出交通事故随时间变化的偏移趋势。交通事故数据平均中心的计算公式如下:

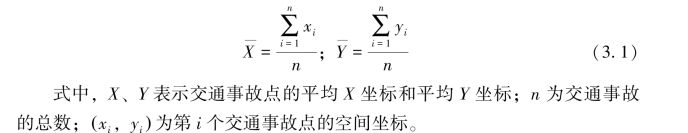
pagenumber_ebook=49,pagenumber_book=42

研究区域MN17，人口普查区面积为2.805km2，2015年至2018年共发生交通事故18414起，平均每平方公里发生6565起，是曼哈顿区平均水平的2.23倍。交通事故的空间分布如图3.6所示，红色点为交通事故点，从图中可以看出交通事故几乎全部分布在道路上。

使用平均中心法(MC)和标准差椭圆法(SDE)对MN17区的交通事故的空间分布特征进行整体描述(刘尧，2019)。通过计算，可以得到MN17区2015—2018年交通事故点的平均中心，如图3.6中绿色圆点所示。查阅地图发现，平均中心位于第六大道和西44街交叉口，处于MN17区的中心，附近地标性建筑为纽约竞技场剧院。

pagenumber_ebook=50,pagenumber_book=43

图3.6　MN17区交通事故的空间分布特征

一组数据点在空间上的聚集性和方向性可以用标准差椭圆(Lefever D W，1926)来描述。以所有事件点的平均中心为基准，计算所有事件点x坐标和y坐标的标准差，然后由标准差的大小来确定椭圆的长半轴和短半轴，此时作出的椭圆就是事件点的标准差椭圆(忻红，2018)。标准差椭圆的计算公式如下(杨迪，2018):

pagenumber_ebook=51,pagenumber_book=44

椭圆的长半轴方向代表事件点在空间上的延伸方向，短半轴的长度则体现了事件点的聚集程度，短半轴越短，说明事件点在空间上越聚集。椭圆的扁率越大，即长短半轴的值之比越大，说明事件点越具有明显的方向性；反之，如果椭圆扁率越小，说明事件点越不具有方向性，当椭圆扁率为1时，说明事件点在空间上的分布不具有方向性。

为了探究交通事故在空间上分布的方向性和集中程度，使用标准差椭圆对其进行研究。通过计算，可以作出标准差椭圆，如图3.6中黄色椭圆所示。通过观察图中标准差椭圆的长半轴方向可以发现，MN17区的交通事故呈现从西南至东北方向扩散的趋势；通过观察标准差椭圆的短半轴可以发现，交通事故在空间上呈聚集分布。从MN17区的自然地理位置及道路交通网络可以发现，交通事故的扩散方向与第五大道、第六大道、第七大道等方向一致，即城市主干道，并且在空间上呈现出聚集分布。

2.Knox时空交互分析

事件是否呈时空聚集分布通常用Knox时空交互检验方法来判断，例如在探究传染病学(刘巧兰，2007)、犯罪学的时空分析研究中，首先计算N个事件点中每两个事件点之间的空间距离Tij和时间间隔Sij。然后选取Knox时空交互检验的空间距离阈值与时间间隔阈值，分别为St和Tt。分别判断N·(N－1)/2个空间距离Tij、时间间隔Sij与相应的空间阈值St、时间阈值Tt之间的大小，如果Sij≤St，则表示事件点i和事件点j在空间上是邻近的，反之是非邻近的；如果Tij≤Tt，则表示事件点i和事件点j在时间上是邻近的，反之是非邻近的。通过对每两个事件点的空间邻近性与时间邻近性进行计算，能够统计出该事件的时空邻近性，见表3.4。

表3.4　事件时空邻近性统计表

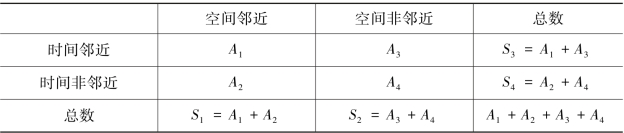
pagenumber_ebook=52,pagenumber_book=45

其中，A1代表两个事件点同时在时间和空间上邻近的个数，A2表示两个事件点只在空间上邻近的个数，A3表示两个事件点只在时间上邻近的个数，A4表示两个事件点在空间上和时间上都不邻近的个数。

通常使用卡方检验方法对事件时空邻近性的统计值进行统计显著性检验(岳瀚，2018)。以交通事故不存在时空交互性为零假设，卡方检验将χ2分布作为其基础，通过χ2分布能够计算得到零假设情况下的p值，然后根据p值的大小判断此零假设是否成立，进而可以得到交通事故的时空分布模式。首先，计算零假设条件下Knox指数实际值A1、A2、A3、A4的期望值E1、E2、E3、E4，见表3.5。

表3.5　Knox指数期望值

pagenumber_ebook=52,pagenumber_book=45

然后，根据Knox指数的实际值和期望值计算卡方值，计算公式如下:

pagenumber_ebook=52,pagenumber_book=45

准确地确定时间和空间阈值是Knox时空交互检验方法的关键所在，时空阈值的大小会影响对事件进行时空聚集性探究的结果，一般通过引用其他领域相应的研究成果作为空间阈值确定的方法，比如许多研究中对不同事件进行时空交互检验时确定空间阈值为100m。但是这种方法对某些事件的检验是不合理的，因为不同事件中事件点之间的距离往往是不同的，比如一个人口普查区的交通事故之间的距离相对较小。因此，有学者对不同事件中空间阈值的确定进行了研究。通过计算事件的平均最邻近距离，然后将其作为空间距离阈值。平均最邻近距离法的计算公式如下:

pagenumber_ebook=53,pagenumber_book=46

式中，dij是事件点i和事件点j之间的空间距离，n为事件点的个数。

将交通事故点的平均最邻近距离作为空间距离阈值，将事故点之间的时间间隔平均值，即平均时间间隔作为时间间隔阈值，来对其进行Knox时空交互检验。通过计算，得到MN17区交通事故点的平均最邻近距离为2.25 m，计算事故点之间的平均时间间隔为6.63小时。在此阈值下，通过统计计算，得出A1＝994861，A2＝968650，A3＝924137062，A4＝918243175；E1＝993132.04，E2＝970378.96，E3＝924138791，E4＝918241446。计算得到此阈值下，χ2＝74.86，p＝5.05×10－18＜0.05。采用置信度为95%的统计显著性对结果进行判断，结果表明，MN17区的交通事故具有时空聚集性和显著的时空交互性，即交通事故在时间上也呈现出聚集模式。

空间探索分析技巧

相关推荐