所谓运算负荷功率，实质上是变电所高压母线上从系统吸取的等值功率。如图3-5所示，变压器二次母线负荷功率为加上变压器损耗得到进入变压器的功率再减掉变电所母线所连线路末端电纳中功率Qc，得到的即为该变电所的运算负荷功率。应该说明的是，在计算运算负荷功率和运算电源功率时变压器损耗和线路电纳功率都是按额定电压计算的。......
2025-09-29
如何用改进欧拉法计算故障切除后电磁功率影响？
【摘要】：应该着重指出，用改进欧拉法对故障切除后的第一个时间段的计算，与用分段计算法不同，电磁功率只用故障切除后的网络方程来求得而不必用故障切除前后的平均值。这是因为改进欧拉法的递推公式中实际已计及了故障切除前瞬间的电磁功率的影响。改进欧拉法和分段计算法的精确度是相同的。如果在输电线路始端发生两相接地短路，线路两侧开关经0.1s同时切除，试用分段计算法和改进欧拉法计算发电机的摇摆曲线，并判断系统能否保持暂态稳定。
设一阶线性微分方程为
且已知t＝t0时刻的初始值x（t0）＝x0，现在求出t＞t0以后满足上述方程的x（t）。暂态稳定计算就是给定了扰动时刻的初值，求扰动后转子运动规律δ（t）的过程，但是在等号右边的非线性函数中，不显示时间变量t，所以只需求解方程
即可。
在t＝0瞬刻，已给定初值x（0）＝x0，于是可以求得此瞬间非线性函数值f（x0）及x的变化速度
在一个很小的时间段Δt内，假设x的变化速度不变，并等于
则第一个时间段内x的增量Δx为
第一个时间段末（即t1＝Δt）的x值为
知道x（1）的值后，便可求得f（x（1））的值以及
从而求得第二个时间段末（即t＝2Δt）的x值
以后时间段的递推公式为
上述算法的特点是算式简单、计算量小，但不够精确，一般不能满足工程计算的精度要求，必须加以改进。改进后的算法如下。
对于任一时间段，先计算时间段初x的变化速度（例如第一个时间段）
于是可以求得时间段末x的近似值
然后再计算时间段末x的近似速度
最后，以时间段初的初始速度和时间段末的近似速度的平均值，作为这个时间段的不变速度来求x的增量，即
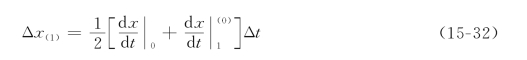
从而求得时间段末x的修正值
这种算法称为改进欧拉法。它的递推公式为
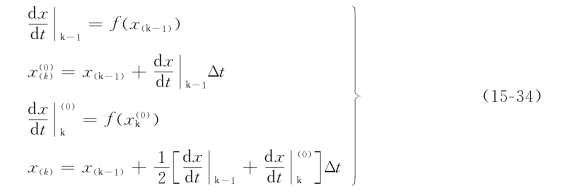
对于一阶微分方程组，递推算式的形式和式（15-34）相同，只是式中的x、f（x）等要换成列相量或列相量函数。
下面，以简单电力系统为例来说明改进欧拉法在暂态稳定计算中的应用。对于转子运动方程
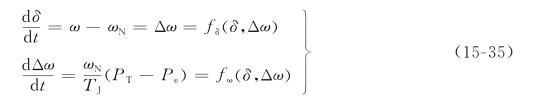
假定计算已进行到第k个时间段。计算步骤及递推公式如下。
确定时间段初的电磁功率
解微分方程求时间段末功角等的近似值（设PT＝P0＝常数）分别为
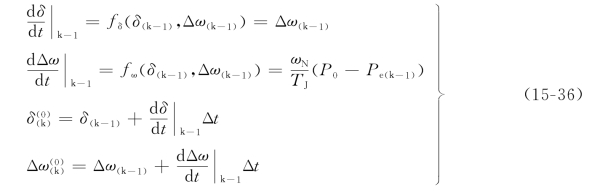
计算时间段末电磁功率的近似值
解微分方程分别求时间段末功角的修正值
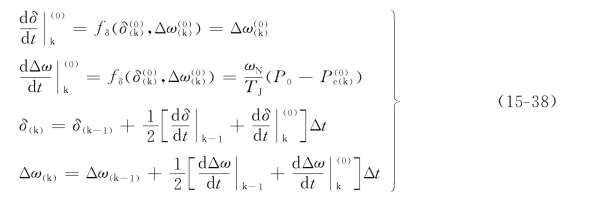
从递推公式可以看到，用改进欧拉法计算暂态稳定，也是把时间分成一个个小段，在每一小段内按等速运动进行微分方程求解，从而求得发电机的转子摇摆曲线。(https://www.chuimin.cn)
应该着重指出，用改进欧拉法对故障切除后的第一个时间段的计算，与用分段计算法不同，电磁功率只用故障切除后的网络方程来求得而不必用故障切除前后的平均值。这是因为改进欧拉法的递推公式中实际已计及了故障切除前瞬间的电磁功率的影响。
改进欧拉法和分段计算法的精确度是相同的。对于简单电力系统（包括某些多机系统的简化计算）来说，分段计算法的计算量比改进欧拉法少得多。
【例15-1】对图13-20所示的系统，发电机的负序电抗x2＝0.2，转子的惯性时间常数TJN＝8s。如果在输电线路始端发生两相接地短路，线路两侧开关经0.1s同时切除，试用分段计算法和改进欧拉法计算发电机的摇摆曲线，并判断系统能否保持暂态稳定。假定线路每回路零序电抗为正序电抗的5倍。
解 由例13-1的计算已得到一些原始运行参数及网络参数，如P0＝1.0，E′0＝1.47，δ′0＝31.54°，x′d＝0.238，xT1＝0.13，xT2＝0.108，xL＝0.586。
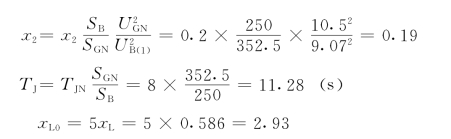
图15-7 序网及短路时的等值电路
（a）负序网络；（b）零序网络；（c）短路时的等值电路
输电线路始端短路时的负序和零序等值网络如图15-7（a）、（b）所示，由图得
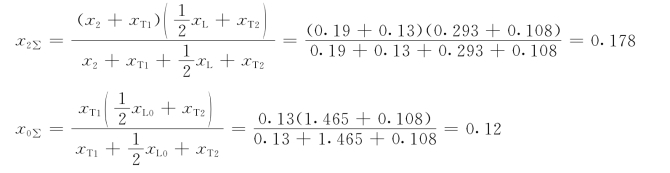
两相接地短路时的附加电抗
等值电路如图15-7（c）所示，系统的转移电抗和功率特性分别为
故障切除后系统的转移电抗及功率特性为
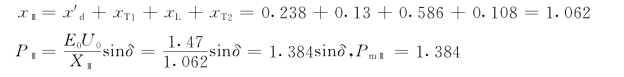
（1）用分段计算法计算。
第一个时间段
第二个时间段
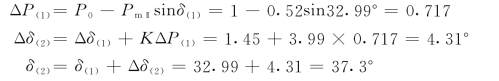
第三个时间段开始瞬间，故障被切除，故
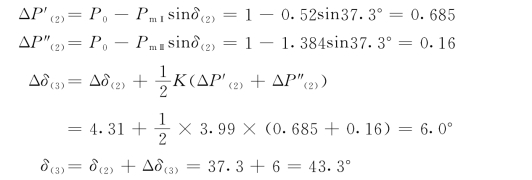
以后时间段的计算结果列于表15-1中。
表15-1 发电机转子摇摆曲线计算结果
（2）用改进欧拉法计算。
第一个时间段
第二个时间段末的功角及相对速度分别为δ（2）＝37.32°，Δω（2）＝114.4（°）/s。
第三个时间段开始瞬间切除故障，应该用切除故障后的网络来求电磁功率，即
以下的计算结果列于表15-1中。由表可以绘出发电机转子摇摆曲线，如图15-8所示。从表及图可以看出，两种算法的结果是极接近的，但分段计算法的计算量少得多。
相关文章
- 详细阅读
-
自动励磁调节器对功率特性的影响详细阅读
图13-18自动励磁调节器对功率特性的影响发电机装设自动励磁调节器后，当功角增大、UG下降时，调节器将增大励磁电流，使发电机电势Eq增大，直到端电压恢复（或接近）整定值UG0为止。为了定性分析调节器对功率特性的影响，用不同的Eq值，做出一组正弦功率特性族，它们的幅值与Eq成正比例，如图13-18所示。实际上，一般的励磁调节器并不能完全保持UG不变，因而UG将随功率P及功角δ的增大而有所下降。......
2025-09-29
-
高斯-塞德尔法潮流计算方法详解详细阅读
应用高斯—塞德尔法进行潮流计算的步骤如下：根据网络结构和参数形成节点导纳矩阵YB；迭代计算各节点电压对PQ节点的处理（i＝1，2，…，n－1）是已知的，因此PV节点的电压初值取为并且在每次迭代完均要修正，具体方法见PV节点。这一迭代过程一直进行到满足收敛条件为止。因为PV节点已知的是Pi、Ui，所以迭代初值应设为然后应用式进行计算，并且作如下修正：a.修正节点电压。......
2025-09-29
-
对称分量法在不对称短路计算中的应用详细阅读
现以图11-3所示简单电力系统为例来说明应用对称分量法计算不对称短路的一般原理。应用对称分量法将这组不对称电势源分解成正序、负序和零序三组对称分量，如图11-4所示。它说明了各种不对称短路时各序电流和同一序电压间的相互联系，表示了不对称短路的共性。根据不对称短路的类型可以得到三个说明短路性质的补充条件，它们表示了各种不对称短路的特性，通常称为故障条件或边界条件。......
2025-09-29
-
牛顿-拉夫逊法在潮流计算中的应用详细阅读
用牛顿—拉夫逊法进行潮流计算时，节点导纳矩阵的形成、平衡节点和支路功率计算都和运用高斯—塞德尔法时相同，区别仅在于迭代过程。根据式可得式即是用牛顿—拉夫逊法潮流计算时的功率方程。图4-4是牛顿—拉夫逊法潮流计算的流程图。给定值为容许误差ε＝10－5试用牛顿—拉夫逊法计算潮流分布。......
2025-09-29
-
变频器功率需按电动机功率以上进行配置，对自动详细阅读
但是，由于各个厂家的具体设计方式不一样，因此变频器的功率需要通过计算仔细确认，同时需要通过试验进行确认。拖动方式 以图8-4-1变频电路为例，对于全变频方式，自动扶梯全程采用变频器拖动。1）变频器功率需按大于电动机功率进行配置。变频器功率大，使用寿命相对较短；自动扶梯发电的再生能量通过电阻消耗，浪费能源；制动电阻功率大，发电时产生的热量对楼宇空调系统有影响。......
2025-09-29
-
安全隐患清单：自动扶梯电磁辐射、电路接地故障详细阅读
3）相邻盖板部件导致的割破危险。6）围裙板和梯级之间夹住的危险。控制电路接地不良，导致漏电保护开关无法起作用，也会造成人员触电的危险。安全功能失效，产生故障导致不能停梯也会造成危险。自动扶梯正常运行期间可能产生电磁辐射，影响建筑物内的其他设备。变频控制系统中由于变频器的选用不当，令其产生较大的电磁辐射。2）受到外界的电磁辐射危险。在危险状态下，如超速、逆转，发生夹伤事故时，如不......
2025-09-29
-
用电势表示的功率特性详细阅读
1．用q轴电势Eq、E′q、UGq表示的功率特性由凸极发电机供电的简单电力系统的相量图如图13-19所示。应用相量图可求出用电势和功角表示的Id，即将式中的Iq及式中的Id代入式中，经整理后可得图13-19凸极发电机供电的简单电力系统相量图这些算式与一样，都包含磁阻功率项，而且当电势、电压均为常数时，功率与功角δ成非正弦的关系。应用上述公式计算功率特性时，须要根据给定的运行条件去确定E′q0、UGq0的值。......
2025-09-29
相关推荐