随机森林在运算量没有显著提高的前提下提高了预测精度。随机森林对多元共线性不敏感，结果对缺失数据和非平衡的数据比较稳健，可以很好地预测多达几千个解释变量的作用，被誉为当前最好的算法之一。随机森林是一个树型分类器的集合。随机森林在建立模型以及进行预测的具体步骤如图6-8所示。图6-8随机森林建模预测步骤①用N表示原始训练集样本的个数，用M表示变量的数目。这也是随机森林的一个非常重要的优点和特点。......
2023-06-28
分段计算法：提高运动计算精度的方法
【摘要】：分段计算法就是把时间分成一个个小段，在每一个小段时间内，把变加速运动近似地看成是等加速运动来解。为了提高计算精度，我们取时间段初和时间段末的加速度的平均值，作为计算每个时间段速度增量的加速度。图15-5切除故障瞬间的过剩功率图15-6转子摇摆曲线1—稳定；2—不稳定分段计算法的计算精度与所选用的时间段的长短（即步长）有关，Δt太大，固然精度下降；Δt过小，除增加计算量外，也会增加计算过程中的累计误差。
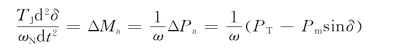
上式中功角对时间的二阶导数为发电机的加速度，当取ω≈1时，转子运动方程为
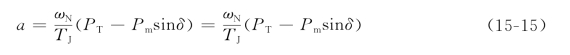
因为δ是时间的函数，所以发电机转子运动是变加速运动。
分段计算法就是把时间分成一个个小段，在每一个小段时间内，把变加速运动近似地看成是等加速运动来解。具体算法如下：
在短路瞬间，发电机电磁功率突然减小，原动机的功率PT＝P0＝常数，转子上出现了过剩功率，ΔP（0）＝PT（0）－Pe（0）＝P0－PmⅡsinδ0，发电机转子获得一个加速度，即
在一个时间段Δt内，近似地认为加速度为恒定值a（0），于是在第一个时间段末，发电机的相对速度和相对角度的增量为
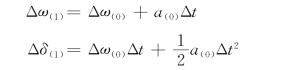
因为发电机的速度不能突变，故Δω（0）＝0，于是
式中，
为一常数。
知道了第一个时间段内的功角增量，即可求得第一个时间段末，第二个时间段开始瞬间的功角值
有了功角新值δ（1）后，便能确定第二个时间段开始瞬间的过剩功率和发电机的加速度分别为
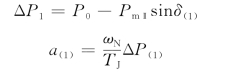
同样假定在第二个时间段内加速度为恒定值a（1），则第二个时间段内角度增量
上式中的相对速度Δω（1）如果按式（15-16）计算，结果并不十分准确。因为在第一个时间段内，加速度毕竟还是变化的。为了提高计算精度，我们取时间段初和时间段末的加速度的平均值，作为计算每个时间段速度增量的加速度。这样，第一个时间段末的速度
将此式代入式（15-19）中，得到
第二个时间段末的角度
同理，我们可以得到第k个时间段的递推公式
设在第m个时间段开始的瞬刻（即第m－1个时间段末）切除故障，发电机的工作点便由PⅡ突然变到PⅢ上。过剩功率也由ΔP′（m－1）＝P0－PmⅡsinδ（m－1），突然变到ΔP″（m－1）＝P0－PmⅢsinδ（m－1）（见图15-5）。在切除故障后的第一个时间段内，计算角度增量时，过剩功率取操作前后瞬间的平均值，即
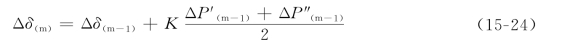
这样，便可以把暂态过程中功角变化计算出来并绘成曲线，如图15-6所示。这种曲线通常称为发电机的转子摇摆曲线。如果功角随时间不断增大（单调变化），则系统在所给定的扰动下是不能保持暂态稳定的。如果功角增加到某一最大值后便开始减小，以后振荡逐渐衰减，则系统是稳定的。
图15-5 切除故障瞬间的过剩功率
图15-6 转子摇摆曲线
1—稳定；2—不稳定
分段计算法的计算精度与所选用的时间段的长短（即步长）有关，Δt太大，固然精度下降；Δt过小，除增加计算量外，也会增加计算过程中的累计误差。Δt的选择应与所研究对象的时间常数相配合，当发电机采用简化模型时，Δt一般可选为0.01～0.05s。
有关电力系统分析的文章
- 详细阅读
-
运动对儿童的好处，运动方法讨论详细阅读
接下来，我觉得还有这么几个问题非常有趣，可以讨论一下。其中最为有害的当属“运动惩罚”。研究发现，孩子运动习惯完全是被父母主导的。小贴士¤运动可以帮助少年儿童增加身高。¤运动有助于预防近视。¤运动有助于控制体型，降低肥胖率。¤运动要遵循少年儿童的生长规律，应循序渐进，不可操之过急。具体见本节的“学龄前儿童与学龄后儿童的运动方法”。......
2023-11-23
-
三十六计走-提高胜率的行动策略详细阅读
“三十六计，走为上计”计语出自《南齐书·王敬则传》：“檀公三十六计，走为上计”。檀公指南朝名将檀道济，相传有《檀公三十六计》，但未见刊本。所谓上计，不是说，“走”在三十六计中是上计，而是说，在敌强我弱的情况下，我方有几种选择：1.求和；2.投降；3.死拼；4.撤退。降则全败，和则半败，走则未败。......
2023-08-13
-
量子遗传优化算法的优化方法详细阅读
量子遗传算法是一种将遗传算法和量子计算相结合的概率优化方法，两者相互作用。量子遗传算法是一种将量子比特的概率幅用于染色体编码，用量子门的调整操作来实现染色体更新，以完成进化搜索的方法。量子遗传算法的流程如下：初始化种群Q，随机生成n个用量子比特编码的染色体。......
2023-06-29
-
社会网络算法的优化方法详细阅读
1）BA网络算法初始设定m0个孤立节点。此算法来自于对分子网络中蛋白质组织结构的分析。研究发现，对于交互和规律的网络来说，高度连接的蛋白质连接被系统的抑制，然而在那些处于高度连接和稀少连接之间的蛋白质结构却没有被抑制。表3-1算法1表3-2算法23）中心分析中心性分析用来检测网络中的关键点以及对网络元素进行排序。......
2023-07-02
-
提高睡前肌肉放松的方法详细阅读
睡前是肌肉放松练习的好时机，肌肉放松有利于更快更好地进入睡眠，当然有利于肌体的恢复。下面介绍一组睡前肌肉放松练习，以使关节的灵活性得到提高。5．站立，两臂在体前放松甩动并抖动，以放松上肢肌肉。9．床上放松下肢。球形滚动是放松背部肌肉比较安全的方法，可减轻腰痛症状。11．仰卧身体，目视天花板，放松全身肌肉，做腹式深呼吸运动10次。......
2023-11-08
-
提高耐力素质的常见方法详细阅读
耐力素质练习的方法较多，而且各种方法都有其各自的特点。总的来说，这些特点基本上又体现在耐力素质练习过程中，在练习强度、持续时间、间歇时间与方式、重复次数等因素的组合与变化上。目前，常用的耐力练习方法主要有以下几种。图4-2耐力素质练习的一般方法（一）持续练习法持续练习法是指在相对较长的时间里，以较为恒定的强度持续地进行练习的方法。但是练习时的强度较小，而且比较恒定，变化不大，一般在60%的强度上下波动。......
2023-11-02
-
孩子运动的好处：增进亲子互动，提高学习效率详细阅读
体育运动不但对于孩子的身体健康很有帮助，还可以增进亲子间的互动，对孩子的成长是很有好处的。虽然做这些运动会占用孩子的学习时间，但是，运动后，孩子的注意力会变得更加集中，不容易被外界干扰，学习效率更高，更容易取得好成绩。......
2024-03-03
相关推荐