在计算机实习过程中，我深入了解了实际工作中的技术应用，提升了编程能力和团队协作意识，同时也积累了珍贵的实践经验，对未来职业发展更加充满信心。......
2025-04-09
如何利用等面积定则计算转子动能？
【摘要】：在标么值计算中，可以认为转子在加速过程中获得的动能增量就等于面积Aabce。当转子由δc变动到δmax时，转子动能增量为由于ΔPa＜0，上式积分为负值，也就是说，动能增量为负值，这意味着转子储存的动能减小了，即转速下降了，减速过程中动能增量所对应的面积称为减速面积，如图中的阴影面积Aedfg。式也可写成即加速面积等于减速面积，这就是等面积定则。同理，根据等面积定则，可以确定摇摆的最小角度δmin，即根据式求得。
从前面的分析可知，在功角由δ0变到δc的过程中，原动机输入的能量大于发电机输出的能量，多余的能量将使发电机转速升高并转化为转子的动能而储存在转子中；而当功角由δc变到δmax时，原动机输入的能量小于发电机输出的能量，不足部分由发电机转速降低而释放的动能转化为电磁能来补充。
转子由δ0到δc时，过剩转矩所做的功为
用标么值计算时，因发电机转速偏离同步速度不大，ω≈1，于是
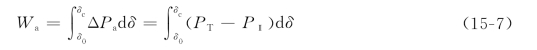
上式右边的积分，代表P-δ平面上的面积，如图15-3阴影部分的面积Aabce。在不计能量损失时，加速期间过剩转矩所做的功，将全部转化为转子动能。在标么值计算中，可以认为转子在加速过程中获得的动能增量就等于面积Aabce。这块面积称为加速面积。当转子由δc变动到δmax时，转子动能增量为
(https://www.chuimin.cn)
由于ΔPa＜0，上式积分为负值，也就是说，动能增量为负值，这意味着转子储存的动能减小了，即转速下降了，减速过程中动能增量所对应的面积称为减速面积，如图中的阴影面积Aedfg。
显然，根据能量守恒原理，动能的增量应等于0，即
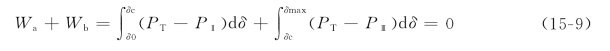
应用这个条件，并将PT＝P0，以及PⅡ和PⅢ的表达式（15-4）、式（15-6）代入，便可求得δmax。式（15-9）也可写成
即加速面积等于减速面积，这就是等面积定则。同理，根据等面积定则，可以确定摇摆的最小角度δmin，即根据式（15-11）求得。
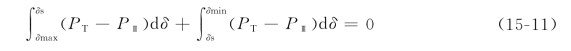
相关文章
- 详细阅读
- 详细阅读
-
如何利用仿真辅助技术提升工作效率？详细阅读
图3-48不同导航数据更新率下仿真得到的弹药射击精度从图3 -48 可知, 随着导航数据更新率的增大, 纵向标准差和CEP 呈现出逐渐增大的变化趋势, 受随机干扰的影响, 中间会出现振荡。......
2025-09-29
- 详细阅读
- 详细阅读
- 详细阅读
- 详细阅读
-
发电机转子的运动方程详细阅读
从前面几节的讨论中可以看到，电力系统受扰动后发电机之间相对运动的特性，表征电力系统稳定的性质。为了较准确和较严格地分析电力系统的稳定性，必须首先建立描述发电机转子运动的动态方程—发电机转子运动方程。这一节，将导出适合电力系统稳定计算用的发电机转子运动方程。发电机转子运动方程，是电力系统稳定分析计算中最基本的方程。......
2025-09-29
相关推荐