磁脱扣器的静态场分析采用三维有限元方法,借助ANSYS有限元分析软件进行,包括载流导体内的电流场分析和脱扣器的磁场分析。脱扣器的三维磁场计算完毕后,与载流导体匝链的磁链ψ采用式(4-1)进行计算。图4-4 磁脱扣器载流导体电流密度分布在有限元分析中,模型的剖分对计算结果的精度有至关重要的影响,若剖分不合理,往往会造成很大的误差,甚至可达20%以上。......
2023-06-15
从电力系统运行可靠性要求出发,我们不能允许电力系统运行在稳定极限的附近,否则,运行情况稍有变动或者扰动,系统便会失去稳定。为此,我们要求电力系统有相当的稳定度。稳定度的大小,通常用稳定储备系数来表示,即

要求电力系统运行时具有多大的储备系数,必须从技术和经济等方面综合考虑。若储备系数定得较大,则要减小正常运行时发电机输送的功率P0(当稳定极限变化不大时)。因而限制了输送能力,恶化输电的经济指标。储备系数定的过小,虽然可以增大正常运行的输送功率,但运行的安全可靠性较低,若出现稳定破坏事故,将造成经济上的巨大损失。电力系统不仅要求正常运行下有足够的稳定储备,而且要求在非常运行方式下(例如双回路的一回路被切除,有待重新投入。这时系统的联系被削弱了,即Xd∑增大了,Psl减小),也应有一定的稳定储备,但稳定储备系数可以小一些。
我国现行《电力系统安全稳定导则》规定:正常运行方式和正常检修运行方式下,KP≥(15%~20%);事故后运行方式和特殊运行方式下,KP≥10%。
电力系统静态稳定实际计算的目的,就是按给定的运行条件,求出以运行参数表示的稳定极限,从而计算出该运行方式下的稳定储备系数,检验它是否满足规定的要求。
从本章第二节可以看出,稳定极限不等于功率极限,并且由于自动励磁调节器的调节作用,稳定极限的求解过程要比功率极限复杂,但从本章第二节中看出,根据励磁调节器的调节能力,可以将求解问题简单化。
(1)将功率极限代替稳定极限。确定发电机的模型(即以何种电势作为常量),然后根据给定的运行方式,进行潮流计算,求出发电机的电势,计算功率特性和功率极限Pm,然后用下列公式计算静态稳定储备系数。
![]()
(2)按某一种电势为常量的功率特性求出稳定极限角度(如图14-8中的点6对应于δEqm,点4对应于δE′qm),将此稳定极限角度代入按另一种电势为常量表示的功率特性中(如图14-8中按PGU0变化的曲线),求出相应的稳定功率Psl,用公式(14-43)计算静态稳定储备系数。
【例14-2】一简单电力系统,已知各元件参数如下:xq=0.8,x′d=0.3,xTL=0.61,无限大系统母线电压为U0=1.0,![]() ,试计算当发电机有励磁调节,E′q=E′q0=常数时的静态稳定储备系数。(均为统一基准下的标么值)
,试计算当发电机有励磁调节,E′q=E′q0=常数时的静态稳定储备系数。(均为统一基准下的标么值)
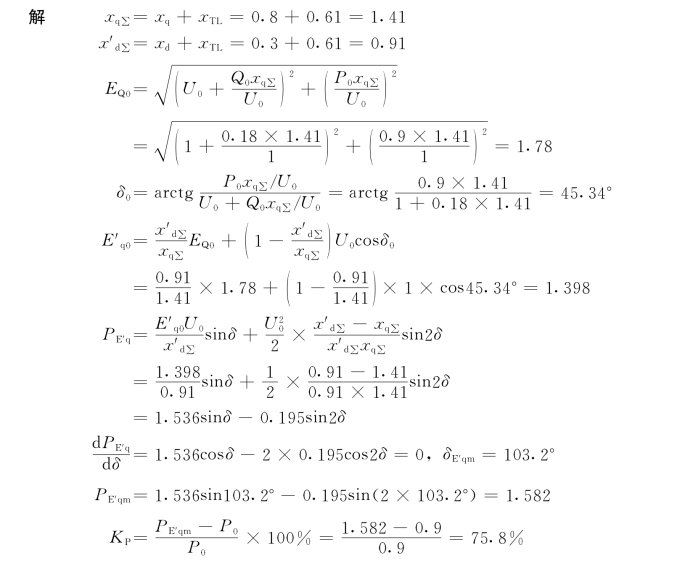
【例14-3】有一简单电力系统,其中发电机为隐极机,xd=1.0,xTL=0.3(均以发电机额定功率为基准值)。无限大系统母线电压为![]() 其等值电路如图14-9所示。如果在发电机端电压为1.05时,发电机向系统输送的功率为0.8,没有进行励磁调节。试计算此时系统的静态稳定储备系数。
其等值电路如图14-9所示。如果在发电机端电压为1.05时,发电机向系统输送的功率为0.8,没有进行励磁调节。试计算此时系统的静态稳定储备系数。

图14-9 例14-3的等值电路
解 设发电机端电压![]() 与无限大系统电压
与无限大系统电压![]() 之间的夹角为δG0。
之间的夹角为δG0。
(1)求δG0。
据![]() 得
得

(2)求系统通过的电流![]()
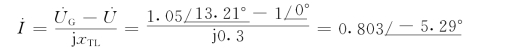
(3)计算![]()
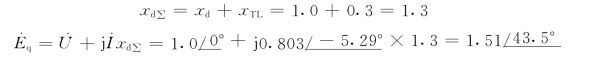
所以![]()
则![]()
【例14-4】求例13-2两机电力系统中发电机G-1的静态稳定储备系数。
解 利用例13-2中的计算结果,则

有关电力系统分析的文章

磁脱扣器的静态场分析采用三维有限元方法,借助ANSYS有限元分析软件进行,包括载流导体内的电流场分析和脱扣器的磁场分析。脱扣器的三维磁场计算完毕后,与载流导体匝链的磁链ψ采用式(4-1)进行计算。图4-4 磁脱扣器载流导体电流密度分布在有限元分析中,模型的剖分对计算结果的精度有至关重要的影响,若剖分不合理,往往会造成很大的误差,甚至可达20%以上。......
2023-06-15

在发电机装设了励磁调节器之后,电力系统静态稳定的情况,与无励磁调节的不同。下面以简单电力系统为例,对电力系统静态稳定作一简要评述,以便简化计算中关于发电机模型处理问题,并有较清晰的理解。图14-8电力系统静态稳定的一般情况无励磁调节的发电机在运行情况缓慢变化时,发电机励磁电流保持不变,即发电机电势Eq=Eq0=常数。电力系统静态稳定极限,将由SEq=0确定,它与功率极限PEqm相等,即由图14-8的点1确定。......
2023-06-15

极端情况下,电力系统会变得不稳定。众所周知,现有的电力系统在电力产量和负载需求之间缺少密切的相关性。美国曾在20世纪发现,如果将6%~12%的发电容量作为能量储存系统安装,那么电网的运行将是最高效的。输入功率和释放功率的大小则与能量转换器的特性有关。换句话说,采用的储能装置和能量转换器的特性决定了能量储存的动态特性。......
2023-06-23

每台主机都分配有一个唯一的二进制编号,称为IP地址。IPV4的IP地址按8位一组分节转换成十进制数并用小数点分隔,这种表示法称为“点分十进制数”表示法,如10101100 00010000 00000000 01100101表示成点分十进制数为172.16.0.101。网络号为127的IP地址不能指派给主机,它被保留用于环路测试。A、B、C类IP地址默认的子网掩码分别是:255.0.0.0、255.255.0.0和255.255.255.0。在配置IP地址时,要指定“默认网关”的IP地址。友情提示●具体IP地址的静态配置方法参考模块一的相关内容。......
2023-10-19

电压静态稳定性计算与负荷增长方式、电网运行方式和发电机功率增长方式、发电方式和潮流断面增长方式等因素密切相关。本节结合电网运行特点和高压直流输电系统运行特点,在不同的视角下进行交直流电网的电压稳定裕度计算。......
2023-06-29

因为电压稳定与无功功率的强相关性,所以风电场引起的电压稳定性降低或电压崩溃现象在本质上与常规电力系统电压失稳的机理是一致的。稳态情况下,风电并网的一个显著特点就是引起接入点的稳态电压上升。也就是说,风电并网对电网静态电压稳定性的影响可以是正面的也可以是负面的,它跟风力发电机的运行点密切相关。......
2023-06-23

例如,当负荷点的运行电压过低或异步电动机的机械负荷过重时,异步电动机会迅速减速以致停转,从而破坏了负荷的正常运行。因此,负荷稳定问题,也是电力系统稳定性的一个重要方面。图13-10负荷稳定的概念现在以一台异步电动机为例来说明负荷静态稳定的概念。如果扰动产生负的ΔS,运行点也将回到点a,所以在点a的运行是稳定的。因此,可以用ΔM/ΔS>0作为负荷静态稳定的判据。......
2023-06-15

1.线性求解器SAMCEF Linear线性求解器属于通用的有限元分析软件包,其功能包括线性静态、线性动力学和屈曲稳定性分析,以及动力响应和随机响应分析。......
2023-10-27
相关推荐