大型电力系统的供电地区幅员宽广，电源和负荷的分布情况比较复杂，频率调整难免引起网络中潮流的重新分布。图6-7互联系统的功率交换图6-7表示系统A和B通过联络线组成互联系统。因此，对于系统A有对于系统B有互联系统应有相同的频率，故，ΔfA＝ΔfB＝Δf。当A、B两系统都进行二次调整，而且两系统的功率缺额又恰同其单位调节功率成比例，即满足条件时，联络线上的交换功率增量ΔPAB便等于零。这时，系统频率质量无法保证。......
2025-09-29
不计发电机组阻尼，风电场转子系统的振动研究
【摘要】：当SEq＜0时，特征值p1、p2为两个实数，其中一个为正实数，所以电力系统受扰动后，功角偏差Δδ最终以指数曲线的形式随时间不断增大，因此系统是不稳定的。这种丧失稳定的形式称为非周期性地失去同步。称为实用判据，常被应用于简单电力系统和一些定性分析的实用计算中。在稳定工作范围内，自由振荡的频率为图14-2fe、SEq随δ的变化这个频率通常又称为固有振荡频率。
发电机的转子运动方程为
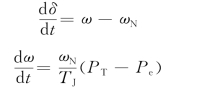
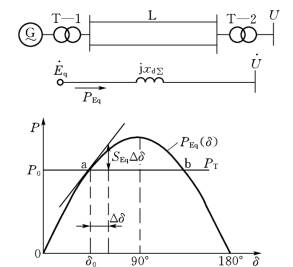
图14-1 简单电力系统及其功角特性
发电机的电磁功率方程为
将上式代入到转子运动方程中去，得到简单电力系统的状态方程为
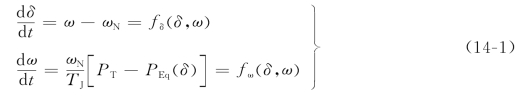
由于PEq（δ）中含有sinδ，所以方程是非线性的。如果扰动很小，可以在平衡点，例如在点a对应的δ0附近将PEq（δ）展开成泰勒级数
略去二次及以上各项得到
因为PEq（δ0）＝P0，所以SEqΔδ为受扰动后功角产生微小偏差引起的电磁功率增量，即
从ΔPe的表达式可以看到，略去功角偏差的二次项及以上各项，实质上是用过平衡点a的切线来代替原来的功率特性曲线（见图14-1），这就是线性化的含义。
将式（14-2）代入式（14-1），并且令ω＝ωN＋Δω，于是得到小扰动方程
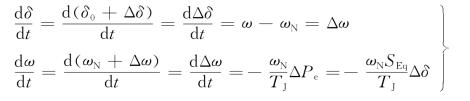
写成矩阵的形式为
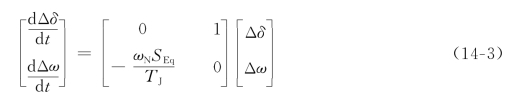
对于这样的二阶微分方程组，其特征值很容易求得，即从下面的特征方程
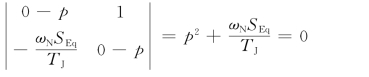
解出
所以，方程组的解为
(https://www.chuimin.cn)
为确定SEq的值，要进行给定运行方式的潮流计算。例如给定系统电压U0、发电机送到系统的功率P0、Q0，算出Eq0、δ0，于是可算得
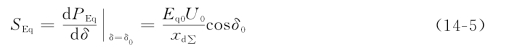
代入式（14-4），即可确定特征值p1、p2，从而判断系统在给定的运行条件下是否具有静态稳定性。
从式（14-4）可以看到，TJ和ωN均为正数，而SEq则与运行情况有关。当SEq＜0时，特征值p1、p2为两个实数，其中一个为正实数，所以电力系统受扰动后，功角偏差Δδ最终以指数曲线的形式随时间不断增大，因此系统是不稳定的。这种丧失稳定的形式称为非周期性地失去同步。当SEq＞0时，特征值为一对共轭虚数
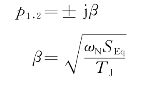
方程组的解为
从实际意义出发，Δδ（t）应为实数，因此kδ1和kδ2应为一对共轭复数。设kδ1＝A＋jB，kδ2＝A－jB，于是
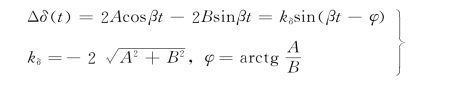
由此可知，电力系统受扰动后，功角将在δ0附近作等幅振荡。从理论上说，系统不具有渐近稳定性，但是考虑到振荡中由于摩擦等原因产生能量消耗，可以认为振荡会逐渐衰减，所以系统是稳定的。
由以上分析可以得出简单电力系统静态稳定的判据为
从式（14-5）可以看到，当系统运行参数δ0＜90°时，系统是稳定的。当δ0＞90°时，系统是不稳定的。所以用运行参数表示的稳定判据为
稳定极限情况为
与此对应的稳定极限运行角
与此运行角对应的发电机输出的电磁功率为
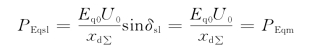
这就是系统保持静态稳定时发电机所能输送的最大功率，把PEqsl称为稳定极限。在上述简单电力系统中，稳定极限等于功率极限。
称为实用判据，常被应用于简单电力系统和一些定性分析的实用计算中。在稳定工作范围内，自由振荡的频率为
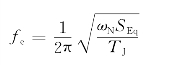
图14-2 fe、SEq随δ的变化
这个频率通常又称为固有振荡频率。它与运行情况即SEq有关，其变化如图14-2所示。从图中可以看出，随着功角的增大，SEq减小，fe减小，当δ＝90°时，SEq＝0，fe＝0，即电力系统受扰动后功角变化不再具有振荡的性质，因而系统将会非周期地丧失稳定。
相关文章
- 详细阅读
-
梯级系统的设计与配置优化详细阅读
一般采用F级绝缘、IP54外壳保护等级。各品牌对公共交通型自动扶梯的动力配置不尽相同，但一般以80%左右的制动载荷作为额定载荷计算电动机功率，通常比普通自动扶梯高20%以上。减速箱 普通自动扶梯多采用造价较低的单级蜗轮蜗杆减速箱。常采用的有全齿轮减速箱、一级齿轮一级蜗轮的减速箱。减速箱的工作寿命设计应不小于140000h。梯级链条的安全系数应不小于5。一般要求在制动载荷条件下，销轴比压不大于25N/mm2。......
2025-09-29
-
发电机转子的运动方程详细阅读
从前面几节的讨论中可以看到，电力系统受扰动后发电机之间相对运动的特性，表征电力系统稳定的性质。为了较准确和较严格地分析电力系统的稳定性，必须首先建立描述发电机转子运动的动态方程—发电机转子运动方程。这一节，将导出适合电力系统稳定计算用的发电机转子运动方程。发电机转子运动方程，是电力系统稳定分析计算中最基本的方程。......
2025-09-29
-
迫击炮武器系统的发展历程详细阅读
由于这种曲射火炮具有优势, 各国开始重视迫击炮的研制和发展。第二次世界大战以来, 随着科学技术的进步, 迫击炮的发展日趋成熟, 迫击炮的性能得到较大提高。迫击炮弹是伴随着迫击炮的发展而发展的。迫击炮弹由早期的近程超口径长炮榴弹逐渐发展为适口径多弹种的弹药。......
2025-09-29
-
智能产品的理论研究详细阅读
例如最近备受关注的话题：“人机大战”即智能产品AlphaGo对阵李世石，就是智能产品具有学习能力的典型。图1-2智能产品AlphaGo对阵李世石3.记忆和思维能力一些智能产品能够存储感知的外部世界的信息，并且能够对信息进行再分析，有选择地消化吸收，并对信息展开联想且能自己做出相对应的判断。......
2025-09-29
-
智能动感单车研究的方法详细阅读
（三）系统的项目方法智能化的运动锻炼器械和它的服务体系设想实现其规模较大且其涉及的要素繁多，是较为复杂化的一个体系。（四）案例的分析方法通过将互联网的技艺能力作为基础后开启的智能化动感自行车的设想实现，和其服务的客户端的设想实现作为方案例子，来探讨以互联网的技艺能力作为基础后其健身类器械的详细设想实现与详细运用方略。......
2025-09-29
-
电力系统的组成及其重要性详细阅读
为了保证一次系统的正常、安全、可靠、经济地运行，还需要各种信号监测、调度控制、保护操作等系统，它们也是电力系统中不可缺少的部分，通常称为二次系统。电力系统中输送和分配电能的变压器和电力线路构成电力网。在交流电力系统中，各组成部分都是三相的，一般用单线图来表示三相交流电力系统各元件间的电的联系。在交流电力系统内或者两个交流电力系统之间嵌入直流输电系统，便构成了现代交、直流联合系统。......
2025-09-29
-
供配电系统的组成分析详细阅读
电能是由发电部门的发电机产生的，这些电能需要通过供配电系统传输给用户。从发电部门的发电机产生电能开始到电能供给最终用户，电能经过了电能的产生、变换、传输、分配和使用环节，这些环节组成的整体称为电力系统。电网是电力系统的一部分，它不包括发电部门和电能用户。......
2025-09-29
相关推荐