首页历史故事发电机转子的运动方程

发电机转子的运动方程

2023-06-15 历史故事版权反馈

【摘要】：从前面几节的讨论中可以看到，电力系统受扰动后发电机之间相对运动的特性，表征电力系统稳定的性质。为了较准确和较严格地分析电力系统的稳定性，必须首先建立描述发电机转子运动的动态方程—发电机转子运动方程。这一节，将导出适合电力系统稳定计算用的发电机转子运动方程。发电机转子运动方程，是电力系统稳定分析计算中最基本的方程。

从前面几节的讨论中可以看到，电力系统受扰动后发电机之间相对运动的特性，表征电力系统稳定的性质。为了较准确和较严格地分析电力系统的稳定性，必须首先建立描述发电机转子运动的动态方程—发电机转子运动方程。这一节，将导出适合电力系统稳定计算用的发电机转子运动方程。

发电机转子的运动状态可用下式表示

式中　J——转动惯量，kg·m·s2；

　　　α——角加速度，rad/s2；

　　　ΔMa——净加速转矩，ΔM＝MT－Me（MT为原动机的转矩，Me为发电机输出的电磁转矩），kg·m。

若以Θ表示从某一固定参考轴算起的机械角位移（rad），Ω表示机械角速度（rad/s），

则有于是可以得到转子运动方程

由电机学知道，如果发电机的极对数为p，则实际空间的几何角、角速度、角加速度与电气角θ、电气角速度ω、加速度α之间有如下关系：

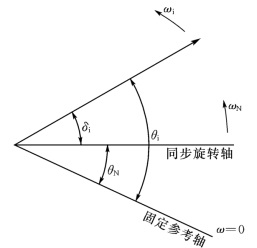
pagenumber_ebook=236,pagenumber_book=229

pagenumber_ebook=236,pagenumber_book=229

图13-11　参考轴与角度

图13-11为以电气量表示的各发电机转子轴线的位置。以某一固定参考轴表示的发电机电气角位移为

如果用某一个以同步速度旋转的轴作为参考轴，则可得

pagenumber_ebook=236,pagenumber_book=229

式中　δi——第i台发电机相对于同步旋转的角位移；

　　　Δωi——相对于同步旋转轴的角速度。

对式（13-11）两边对时间求导得

pagenumber_ebook=236,pagenumber_book=229

再次求导后得

pagenumber_ebook=236,pagenumber_book=229

计及可得转子运动方程为如果选基准转矩则上式两边除以MB得

pagenumber_ebook=237,pagenumber_book=230

我们定义为惯性时间常数。

通常制造厂家提供的发电机组的数据是飞轮转矩（或称回转力矩）GD2，它和额定惯性时间常数TJN之间的关系为

pagenumber_ebook=237,pagenumber_book=230

式中　GD2——飞轮转矩，t·m2；

　　　SN——发电机的额定容量，kVA；

　　　n——发电机的额定转速，r/min。

在电力系统的稳定计算当中，当已选好全系统的基准功率SB时，必须将各发电机的额定惯性时间常数归算为统一基准值下的值，即

有时，须将几台发电机合并成一台等值发电机，合并后的等值发电机的惯性时间常数为

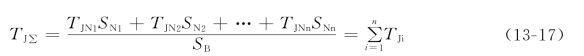
pagenumber_ebook=237,pagenumber_book=230

于是转子运动方程为

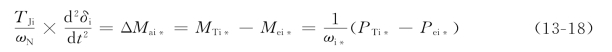
pagenumber_ebook=237,pagenumber_book=230

当ωN＝2πfN时，δi为弧度；当ωN＝360fN时，δi为度。TJi的单位为s。

发电机转子运动方程，是电力系统稳定分析计算中最基本的方程。在多机电力系统中，对于第i台发电机有（略去表示标么值的星号）

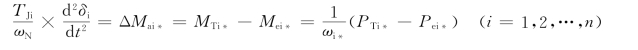
pagenumber_ebook=237,pagenumber_book=230

电力系统受到扰动后发电机之间的相对运动，是用这些方程的解δi（t）－δj（t）来描述的，这些解也是用来判断系统稳定性的最直接的判据。

上述方程中等号右边的不平衡转矩（或功率）是很复杂的非线性函数。等号右边的第一项是第i台发电机的原动机的转矩（或功率），它主要取决于本台发电机的原动机及其调速系统的特性。等号右边的第二项是第i台发电机的电磁转矩（或功率），它不但与本台发电机的电磁特性、励磁调节系统特性等有关，而且还与其他发电机的电磁特性、负荷特性、网络特性等有关，它是电力系统稳定分析计算中最为复杂的部分。