极端情况下，电力系统会变得不稳定。众所周知，现有的电力系统在电力产量和负载需求之间缺少密切的相关性。美国曾在20世纪发现，如果将6%～12%的发电容量作为能量储存系统安装，那么电网的运行将是最高效的。输入功率和释放功率的大小则与能量转换器的特性有关。换句话说，采用的储能装置和能量转换器的特性决定了能量储存的动态特性。......
2023-06-23
电力系统稳定性中的负荷稳定问题
【摘要】：例如，当负荷点的运行电压过低或异步电动机的机械负荷过重时，异步电动机会迅速减速以致停转，从而破坏了负荷的正常运行。因此，负荷稳定问题，也是电力系统稳定性的一个重要方面。图13-10负荷稳定的概念现在以一台异步电动机为例来说明负荷静态稳定的概念。如果扰动产生负的ΔS，运行点也将回到点a，所以在点a的运行是稳定的。因此，可以用ΔM/ΔS＞0作为负荷静态稳定的判据。
在电力系统的负荷中，大部分负荷是异步电动机。由于异步电动机也是一种旋转电机同样存在与转矩平衡有关的运行稳定性。例如，当负荷点的运行电压过低或异步电动机的机械负荷过重时，异步电动机会迅速减速以致停转，从而破坏了负荷的正常运行。停转时，异步电动机吸收的有功功率变得很小，这将使电力系统中发电机输出功率发生变化，从而引起发电机转子间的相对运动，有时还可能导致发电机之间失去同步。因此，负荷稳定问题，也是电力系统稳定性的一个重要方面。
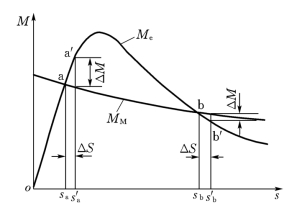
图13-10 负荷稳定的概念
现在以一台异步电动机为例来说明负荷静态稳定的概念。电动机转子上作用着两种转矩：一是电磁转矩，它是推动转子旋转的；二是机械转矩，它是制动性的。在正常运行时，两种转矩相互平衡，电动机保持恒定的转差运行。
我们把电磁转矩—转差特性和机械转矩—转差特性画出来（见图13-10），从图中可以看到有两个平衡点a、b。在点a运行时，如果受到扰动后转差变为s′a，增加了一个微小的增量Δs＝s′a－sa，则电磁转矩将大于机械转矩，转子上产生了加速性的不平衡转矩ΔM＝Me－MM，使电动机的转速增大，转差减小，最终恢复到点a运行。如果扰动产生负的ΔS，运行点也将回到点a，所以在点a的运行是稳定的。
在点b运行时，如果扰动产生正的ΔS，则从图13-10中可以看到，此时，电磁转矩小于机械转矩，转子上产生减速性的不平衡转矩。在此不平衡转矩作用下，电动机转速下降，转差继续增大，如此下去直到电动机停转为止。所以在点b的运行是不稳定的。
从以上的分析可以看到，在点a运行时，转差增量ΔS与不平衡转矩具有相同的符号；而在点b运行时两者符号则相反。因此，可以用ΔM/ΔS＞0作为负荷静态稳定的判据。当用功率的形式表示，机械功率与转差无关且恒定时，极限形式的判据为
有关电力系统分析的文章
- 详细阅读
-
如何计算电力系统的静态稳定性？详细阅读
为此，我们要求电力系统有相当的稳定度。电力系统静态稳定实际计算的目的，就是按给定的运行条件，求出以运行参数表示的稳定极限，从而计算出该运行方式下的稳定储备系数，检验它是否满足规定的要求。试计算此时系统的静态稳定储备系数。据得求系统通过的电流计算所以则求例13-2两机电力系统中发电机G-1的静态稳定储备系数。......
2023-06-15
-
提升电器的电动稳定性详细阅读
电器的电动稳定性是指电器能短时耐受短路电流的作用，且不致产生永久性形变或遭到机械损伤的能力。在短路电流产生的巨大电动力作用下，载流导体以及与工作刚性连接的绝缘件和结构件均可能发生形变乃至损坏，故电动稳定性也是考核电器性能的重要指标之一。此电动力为视闸刀为两端固定的横梁，闸刀断面内的最大应力为因此，开关的电动稳定性是合格的。......
2023-06-30
-
提升电源-电弧系统稳定性的措施详细阅读
如图1-1-15a所示，在电弧焊中，弧焊电源是供电者，焊接电弧是用电者，两者构成“电源-电弧”系统。该系统的稳定性包含如下两方面的含义。这两个交点确定了系统的静态稳定状态。在干扰消失之后，系统能够自动地达到新的稳定平衡，使焊接参数重新恢复。系统自动恢复速度与弧焊电源Uy和电弧Uf之差及回路L有关，Kw越大，电感越小，恢复越快，稳定性越好。......
2023-06-25
-
解析8.7OLED封装问题：稳定性和寿命优化详细阅读
通常，电路的保护或封装的作用是保护有源有机层和敏感性高的阴极金属。图8-15列出了有图8-15 OLED器件的封装问题机半导体所遇到的问题并定义了OLED封装的概念。图8-17 PET塑料衬底上的OLED 3″无源显示器（见彩页）然而，为了使这些应用保持热度，有机器件的封装不能有坚硬的部分。然而，OLED商业应用中对寿命的要求较高，对封装的要求也与上述方法有着明显不同，而获得合适的有抵抗力的OLED保护存在一定难度。......
2023-06-15
-
熔滴过渡形态对电弧稳定性的影响详细阅读
在两个虚线框中以外还有两个标有黑色圆点的结点，即Ⅳ-B、Ⅲ-B，分别表示具有粗熔滴过渡和爆炸过渡同时具有敞开型电弧，这种情况下电弧稳定性居中。表2-3列出了几种代表性常用焊条熔滴过渡形态、电弧类型、电弧稳定性结点位置和电弧稳定性系数值。......
2023-06-30
-
稳定性试验设计及意义探讨详细阅读
在稳定期内实施检测程序，控制不稳定的因素，是确保检测结果有效性的前提和基础。分析方法的稳定性是通过稳定性试验评价获得的。稳定性试验主要是研究样品、样品前处理后的基质、标准溶液在规定条件保管下目标分析物的稳定期限。根据《GB/T 32465—2015化学分析方法验证确认和内部质量控制要求》的规定，在稳定性试验的保管条件及其试验样品数按照表2－11进行研究。......
2023-06-29
-
微波通信的稳定性与特点详细阅读
微波频段占用的频带约300GHz，一套微波中继通信设备可以容纳几千甚至几万条话路同时工作，或传输图像信号等宽带信号。由于微波频段频率高，这些干扰对微波通信的影响极小。因此，微波通信稳定、可靠。微波中继通信采用中继方式可以实现地面上的远距离通信，并且可以跨越沼泽、江河、高山等特殊地理环境。对于数字微波通信系统来说，是利用微波信道传输数字信号，因为基带信号为数字信号，所以称为数字微波通信系统。......
2023-06-27
相关推荐