电控系统由控制柜、变频器、电气配线、开关与插座、维修控制盒、故障显示装置等组成。对室外型自动扶梯，机房需要有强制通风，控制柜内温度不能大于电子器件的最高工作温度。变频器的外壳保护等级应与控制柜相同，室外型自动扶梯不小于IP55；室内型自动扶梯不小于IP43，能适应50℃的工作环境温度。一旦发生火灾，可以降低电缆燃烧时所产生的烟雾对人体的危害。......
2025-09-29
从群体错乱到系统稳定：暂态稳定初探
【摘要】：电力系统具有静态稳定性是稳定运行的必要条件。电力系统受大扰动后能否保持稳定性的问题，乃是暂态稳定研究的内容。下面简要介绍它的初步概念。图13-8暂态稳定的概念在切除线路瞬间，发电机输出的电磁功率由PⅡ曲线上的b确定。如果电力系统受大扰动后功角不断增大，则表明发电机之间已不再同步，系统失去了暂态稳定。因此，可以用电力系统受大扰动后功角随时间变化的特性作为暂态稳定的判据。
电力系统具有静态稳定性是稳定运行的必要条件。但是不能肯定地说，当电力系统受到大的扰动（各种短路、切除输电线路等）时，也能保持稳定运行。电力系统受大扰动后能否保持稳定性的问题，乃是暂态稳定研究的内容。下面简要介绍它的初步概念。
讨论简单电力系统突然切除一回输电线路的情况。如图13-7所示，在正常运行时，系统的总电抗为
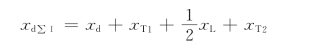
此时的功率特性为
切除一回线路后，系统的总电抗为
相应的功率特性为
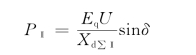
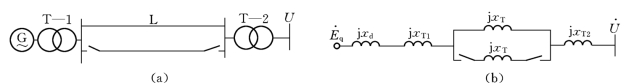
图13-7 切除一回输电线路
如果不考虑发电机的电磁暂态过程和励磁调节作用，即假定Eq保持不变，则由于线路电抗增大，从而功率的幅值减小（见图13-8）。(https://www.chuimin.cn)
线路切除前瞬间，发电机处于正常运行状态，它输出的电磁功率由PⅠ曲线上的点a确定，其值为P0。原动机的功率，在正常运行时与电磁功率相平衡，即PT＝Pe＝P0。
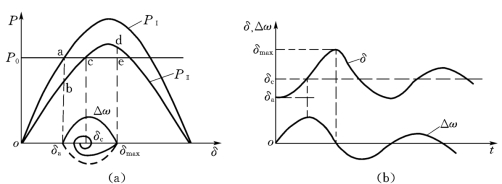
图13-8 暂态稳定的概念
在切除线路瞬间，发电机输出的电磁功率由PⅡ曲线上的b确定。这是由于转子具有惯性，其转速不能瞬时改变，所以线路切除瞬间，功角保持原值不变。由于发电机的工作点由a突然变到点b，它输出的电磁功率突然减小。与此同时，原动机的功率仍然等于原值。这是由于原动机调速器不可避免滞迟，加之在暂态过程的初始阶段转速变化不大，调速器的调节量也很小，为简单起见，假定原动机的功率一直保持不变值。
在切除线路瞬间，原动机功率大于电磁功率，作用在转子上的不平衡转矩（用功率表示为ΔPa＝PT－Pe）是加速性的，因而使发电机加速。于是在送、受端发电机之间出现了正的相对速度，功角开始增大，发电机工作点将由点b向点c变动，发电机输出的电磁功率也逐渐增大。在到达点c以前，虽然加速性的不平衡转矩逐渐减小，但它一直是加速性的，因此相对速度不断增大［见图13-8（a）］。
在点c处，虽然转子上的转矩又相互平衡，但过程并不会到此结束，因为此刻送端发电机的转速已高于受端发电机的转速，由于转子的惯性，功角将继续增大而越过点c。越过点c之后，当功角继续增大时，电磁功率将超过原动机的功率，不平衡转矩加速性变成减速性的了。在此不平衡转矩作用下，发电机开始减速，相对速度Δω也开始减小并在点d达到零值。
在点d，送、受端发电机恢复了同步，功角不再增大，并抵达它的最大值。此刻电磁功率仍大于原动机的功率，发电机仍受减速性的不平衡转矩作用而继续减速。于是发电机的转速开始小于受端发电机的转速，相对速度Δω＜0，功角开始减小，工作点将沿相反方向变动到点c。而且由于惯性作用它将越过点c而在b附近Δω再次等于零，功角不再减小并抵达它的最小值。以后功角又开始增大。由于各种损耗，功角变化将是一种减幅振荡［图13-8（b）］。最后在点c处，同时达到Δω＝0和ΔPa＝0，建立了新的稳定运行状态。
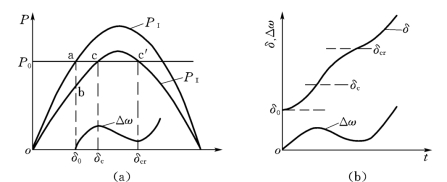
图13-9 失去暂态稳定的情况
可是过程也可能有另外一种结局。如图13-9所示，从点c开始，转子减速，Δω减小。但Δω是大于零的，所以功角仍继续增大。如果Δω还未降到零时，功角已达到临界角（对应于c′），则因为Δω＞0，故功角将继续增大而越过点c′，因而转子上的不平衡转矩又变成加速性的了。于是Δω又开始增加，功角将继续增大，使发电机与受端系统失去同步，破坏了电力系统的稳定运行。
由以上分析可以得到暂态稳定的初步概念：电力系统具有暂态稳定性，一般是指电力系统在正常运行时，受到一个大的扰动后，能从原来的运行状态（平衡点），不失去同步地过渡到新的运行状态，并在新运行状态下稳定地运行。
从以上的讨论中可以看到，功角变化的特性，表明了电力系统受大扰动后发电机转子运动的情况。若功角经过振荡后能稳定在某一个数值，则表明发电机之间重新恢复了同步运行，系统具有暂态稳定性。如果电力系统受大扰动后功角不断增大，则表明发电机之间已不再同步，系统失去了暂态稳定。因此，可以用电力系统受大扰动后功角随时间变化的特性作为暂态稳定的判据。
相关文章
- 详细阅读
-
弹道测量技术：GPS测量系统详细阅读
GPS 整个卫星导航系统包括空间部分、地面支撑系统、用户设备三部分。图4-4弹载接收机组成图弹载接收机GPS 测量系统的特点是可对炮弹或火箭弹进行实时定位, 向地面发送定位信息所需的线路带宽较窄, 被测目标数量不受限制。弹载设备接收GPS 卫星L 波段信号, 经变频放大后, 通过遥测信道转发到地面,在地面完成对GPS 信号的测量和数据处理。地面设备包括GPS 接收设备和数据处理分系统。......
2025-09-29
-
互联系统频率的调节方法详细阅读
大型电力系统的供电地区幅员宽广，电源和负荷的分布情况比较复杂，频率调整难免引起网络中潮流的重新分布。图6-7互联系统的功率交换图6-7表示系统A和B通过联络线组成互联系统。因此，对于系统A有对于系统B有互联系统应有相同的频率，故，ΔfA＝ΔfB＝Δf。当A、B两系统都进行二次调整，而且两系统的功率缺额又恰同其单位调节功率成比例，即满足条件时，联络线上的交换功率增量ΔPAB便等于零。这时，系统频率质量无法保证。......
2025-09-29
-
迫击炮武器系统的发展历程详细阅读
由于这种曲射火炮具有优势, 各国开始重视迫击炮的研制和发展。第二次世界大战以来, 随着科学技术的进步, 迫击炮的发展日趋成熟, 迫击炮的性能得到较大提高。迫击炮弹是伴随着迫击炮的发展而发展的。迫击炮弹由早期的近程超口径长炮榴弹逐渐发展为适口径多弹种的弹药。......
2025-09-29
-
梯级系统的设计与配置优化详细阅读
一般采用F级绝缘、IP54外壳保护等级。各品牌对公共交通型自动扶梯的动力配置不尽相同，但一般以80%左右的制动载荷作为额定载荷计算电动机功率，通常比普通自动扶梯高20%以上。减速箱 普通自动扶梯多采用造价较低的单级蜗轮蜗杆减速箱。常采用的有全齿轮减速箱、一级齿轮一级蜗轮的减速箱。减速箱的工作寿命设计应不小于140000h。梯级链条的安全系数应不小于5。一般要求在制动载荷条件下，销轴比压不大于25N/mm2。......
2025-09-29
-
弹道测量系统：精准测量瞄准目标详细阅读
目前, 常用的弹道探测方式包括雷达探测、惯性导航、卫星导航等。在弹道修正迫击炮弹飞行过程中, 雷达不断探测弹丸实际弹道信息、解算出控制指令信息并发送给弹丸。弹道修正弹的发展方向是 “发射后不管”, 因此这种探测方式在弹道修正技术中并不常用。目前北斗导航系统的导航区域已覆盖全球, 使用民码的定位精度可达10 m, 定速精度可达0.2 m/s, 使用军码可达到更高的定位、定速精度。......
2025-09-29
-
电力系统接线方式详解详细阅读
电力系统的接线方式按供电可靠性分为有备用接线方式和无备用接线方式两种。无备用接线方式是指负荷只能从一条路径获得电能的接线方式。但一级负荷的比重不大，并可为这些负荷单独设置备用电源时，仍可采用这种接线，这种接线方式广泛应用于二级负荷。可见，接线方式的选择要经技术经济比较后才能确定。所选的接线方式在满足安全、优质、经济的指标外，还应保证运行灵活和操作方便、安全。......
2025-09-29
-
如何保证系统无功功率平衡？详细阅读
所谓无功功率的平衡就是要使系统的无功电源所发出的无功功率与系统的无功负荷及网络中无功损耗相平衡。如系统电源所能供应的无功功率仅为∑QGc，则无功功率虽也能平衡，平衡条件所决定的电压将为低于正常的电压U。从而可见，系统中应保持一定的无功功率备用，否则负荷增大时，电压质量仍无法保证。这个无功功率备用容量一般可取最大无功功率负荷的7%～8%。......
2025-09-29
相关推荐