在发电机装设了励磁调节器之后，电力系统静态稳定的情况，与无励磁调节的不同。下面以简单电力系统为例，对电力系统静态稳定作一简要评述，以便简化计算中关于发电机模型处理问题，并有较清晰的理解。图14-8电力系统静态稳定的一般情况无励磁调节的发电机在运行情况缓慢变化时，发电机励磁电流保持不变，即发电机电势Eq＝Eq0＝常数。电力系统静态稳定极限，将由SEq＝0确定，它与功率极限PEqm相等，即由图14-8的点1确定。......
2023-06-15
静态稳定的初步理解
【摘要】：图13-5静态稳定的概念在a点运行时，假定系统受到某种微小的扰动，使发电机的功角产生了一个微小的增量Δδ，由原来的运行值δa变到δa′。由以上的分析，可以得到静态稳定的初步概念：所谓电力系统静态稳定性，一般是指电力系统在运行中受到微小扰动后，独立地恢复到它原来的运行状态的能力。我们看到，对于简单电力系统，要具有运行的静态稳定性，必须运行在功率特性的上升部分。
从以上的分析可知，送端发电机要稳定地与系统同步运行，作用在发电机转子上的转矩必须相互平衡。但是，转矩相互平衡是否就一定能稳定地运行呢？从图13-5可知，平衡点有a、b两个。下面进一步分析这两个平衡点的运行特性。
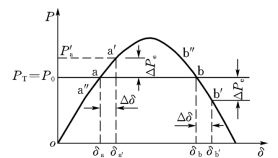
图13-5 静态稳定的概念
在a点运行时，假定系统受到某种微小的扰动，使发电机的功角产生了一个微小的增量Δδ，由原来的运行值δa变到δa′。于是，电磁功率也相应地增加到Pa′。从图中可以看到，正的功角增量Δδ＝δa′－δa产生正的电磁功率增量ΔPe＝Pa′－P0。至于原动机的功率则与功角无关，仍然保持PT＝P0不变。发电机电磁功率的变化，使转子上的转矩平衡受到破坏。由于此时电磁功率大于原动机的功率，转子上产生可制动性的不平衡转矩。在此不平衡转矩作用下，发电机转速开始下降，因而功角开始减小。经过衰减振荡后，发电机恢复到原来的运行点a［见图13-6（a）］。如果在点a运行时受扰动产生一个负值的角度增量Δδ＝δa″－δa，则电磁功率的增量ΔPe＝Pa″－P0也是负的，发电机将受到加速性的不平衡转矩作用而恢复到点a运行。所以在点a的运行是稳定的。
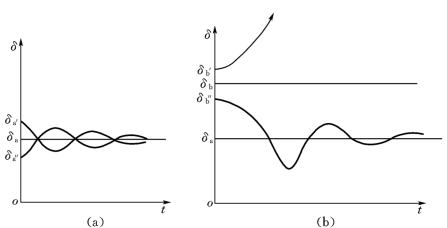
图13-6 小扰动后功角的变化
（a）点a运行；（b）点b运行
点b运行的特性完全不同。这里，正值的角度增量Δδ＝δb′－δb，使电磁功率减小而产生负值的电磁功率增量ΔPe＝Pb′－P0（见图13-5）。于是，转子在加速性不平衡转矩作用下开始升速，使功角增大。随着功角δ的增大，电磁功率继续减小，发电机转速继续增加。这样送端和受端的发电机便不能继续保持同步运行，即失去了稳定。如果在点b运行时受到微小扰动而获得一个负值的角度增量，则将产生正值的电磁功率增量，发电机的工作点将由点b过渡到点a，其过程如图13-6（b）所示。由此得出，点b运行是不稳定的。
由以上的分析，可以得到静态稳定的初步概念：所谓电力系统静态稳定性，一般是指电力系统在运行中受到微小扰动后，独立地恢复到它原来的运行状态的能力。我们看到，对于简单电力系统，要具有运行的静态稳定性，必须运行在功率特性的上升部分。在这部分，电磁功率增量和角度增量总是具有相同的符号。而在功率特性下降部分，ΔPe和Δδ总是具有相反的符号。因此，可以用比值的符号来判别系统在给定的平衡点运行时是否具有静态稳定性，即可以用
作为简单电力系统具有静态稳定性的判据。写成极限的形式为
有关电力系统分析的文章
- 详细阅读
-
研究静态电压稳定性对风电并网的影响详细阅读
因为电压稳定与无功功率的强相关性，所以风电场引起的电压稳定性降低或电压崩溃现象在本质上与常规电力系统电压失稳的机理是一致的。稳态情况下，风电并网的一个显著特点就是引起接入点的稳态电压上升。也就是说，风电并网对电网静态电压稳定性的影响可以是正面的也可以是负面的，它跟风力发电机的运行点密切相关。......
2023-06-23
-
如何计算电力系统的静态稳定性？详细阅读
为此，我们要求电力系统有相当的稳定度。电力系统静态稳定实际计算的目的，就是按给定的运行条件，求出以运行参数表示的稳定极限，从而计算出该运行方式下的稳定储备系数，检验它是否满足规定的要求。试计算此时系统的静态稳定储备系数。据得求系统通过的电流计算所以则求例13-2两机电力系统中发电机G-1的静态稳定储备系数。......
2023-06-15
-
线性静态、动力学与屈曲稳定性分析详细阅读
1.线性求解器SAMCEF Linear线性求解器属于通用的有限元分析软件包，其功能包括线性静态、线性动力学和屈曲稳定性分析，以及动力响应和随机响应分析。......
2023-10-27
-
基于连续型潮流法的交直流输电系统静态稳定性计详细阅读
电压静态稳定性计算与负荷增长方式、电网运行方式和发电机功率增长方式、发电方式和潮流断面增长方式等因素密切相关。本节结合电网运行特点和高压直流输电系统运行特点，在不同的视角下进行交直流电网的电压稳定裕度计算。......
2023-06-29
-
通风机稳定与非稳定工作区的优化详细阅读
因为在这一区间工作时，通风机的工作状态能自动地与管网的工作状态保持平衡，稳定地工作，所以我们把这一区间叫做通风机的稳定工作区。喘振现象发生后，风机运行的声音发生突变，风量和风压急剧地波动，机器及管网强烈地振动，如果不立即停机或采取其他人为措施消除之，将会造成机器严重破坏，故选用通风机时必须注意，应尽量避免在非稳定区工作，绝对禁止在喘振区工作。......
2023-06-22
-
确定液压系统参数的初步步骤详细阅读
系统工作压力p 的确定由于主机的性能和使用场合不同,液压系统的工作压力也不尽相同。因此,系统工作压力的选择取决于尺寸、成本、使用可靠性等多方面因素,一般可参考现有的同类液压系统来初步确定系统工作压力。表8.2常用液压设备工作压力执行元件主要结构参数的确定这里主要确定液压缸的有效工作面积、活塞直径和活塞杆直径,确定液压马达的每转排量。......
2023-06-18
-
静态时序分析的作用及优化方法详细阅读
图6.9 DC的静态时序分析静态时序分析可以不通过动态仿真就确定电路是否满足时间的约束。静态时序分析主要包括3个主要步骤。图6.10 时序路径如图6.11所示，图中共有5个终点，CLK1控制3个终点，共有8条路径。这12条路径被分为3个路径组分别是CLK1、CLK2和默认路径组。图6.11 时序路径组在计算路径延迟时，DC把每一条路径分成时间弧，时间弧描述单元或连线的时序特性。......
2023-06-26
相关推荐