当系统频率略有下降时，负荷的有功功率成正比例自动减小。图中直线的斜率为或用标么值表示图6-2负荷的有功功率—频率静态特性曲线KD、KD*称为负荷的频率调节效应系数或简称为负荷的频率调节效应。在实际系统中KD*＝1～3，它表示频率变化1%时，负荷有功功率相应变化1%～3%。KD*的数值是调度部门必须掌握的一个数据，因为它是考虑按频率减负荷方案和低频率事故时用一次切除负荷来恢复频率的计算依据。......
2023-06-15
综合负荷的阻抗特性分析
【摘要】：在上述两种情况以外的短路计算中，负荷的正序参数常用恒定阻抗表示，即图11-23确定电动机正序阻抗的等值电路式中SLD、ULD——负荷的视在功率和负荷节点的电压。异步电动机是旋转元件，其负序阻抗不等于正序阻抗。我们看到，异步电动机的负序阻抗也是转差的函数。计及降压变压器及馈电线路的电抗，则以异步电动机为主要成分的综合负荷的负序电抗为它是以综合负荷的视在功率和负荷接入点的平均额定电压为基准的标么值。
电力系统负荷主要是工业负荷。大多数工业负荷是异步电动机。由电机学知道，异步电动机可以用图11-23所示的等值电路来表示（图中略去了励磁支路的电阻）。异步电动机的正序阻抗，就是图中机端呈现的阻抗。我们看到，它与电动机的转差s有关。在正常运行时，电动机的转差与机端电压及电动机的受载系数（即机械转矩与电动机额定转矩之比）有关，一般约为百分之几。在短路过程中，电动机端电压下降，将使转差增大，并随着端电压的变化而变化。所以，要准确计算电动机的正序阻抗较为困难。
在短路的实际计算中，对于不同的计算任务制作正序等值网络时，对综合负荷有不同的处理方法。在计算起始次暂态电流时，综合负荷或者略去不计，或者表示为有次暂态电势和次暂态电抗的电势源支路，视负荷节点离短路点电气距离的远近而定。在应用计算曲线来确定任意指定时刻的短路周期电流时，由于曲线制作条件已计入负荷的影响，因此等值网络中的负荷都被略去。
在上述两种情况以外的短路计算中，负荷的正序参数常用恒定阻抗表示，即
图11-23 确定电动机正序阻抗的等值电路
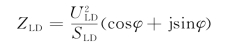
式中 SLD、ULD——负荷的视在功率和负荷节点的电压。
假定短路前负荷处于额定运行状态且cosφ＝0.8，则以额定值为基准的标么阻抗为
为避免复数运算，又可用等值的纯电抗来代表负荷，其值为
分析计算表明，负荷分别用这两种阻抗表示时，所得的计算结果极为接近。
异步电动机是旋转元件，其负序阻抗不等于正序阻抗。当电动机端施加基频负序电压时，流入定子绕组的负序电流将在气隙中产生一个与转子转向相反的旋转磁场，它对电动机产生制动性转矩。若转子相对于正序旋转磁场的转差为s，则转子相对于负序旋转磁场的转差为2－s。将2－s代替图11-23中的s，便可得到确定异步电动机负序阻抗的等值电路。我们看到，异步电动机的负序阻抗也是转差的函数。
为了简化计算，实用上常略去电阻，并取s＝1时，即以转子静止（或启动初瞬间）状态的阻抗模值作为电动机的负序电抗，此刻负序电抗就等于次暂态电抗。计及降压变压器及馈电线路的电抗，则以异步电动机为主要成分的综合负荷的负序电抗为
它是以综合负荷的视在功率和负荷接入点的平均额定电压为基准的标么值。
当系统某处发生不对称短路时，因为异步电动机及多数负荷常常接成三角形，或者接成不接地的星形，所以零序电流不能流通，故不需要建立零序等值电路。
有关电力系统分析的文章
- 详细阅读
-
单导线大地回路的自阻抗和互阻抗分析详细阅读
图11-14示出一“单导线－大地”回路。根据推导得，“单导线－大地”回路的自阻抗为上式中ra——单位长度导线aa的电阻；re——单位长度虚拟导线ee的等值电阻，它是所通交流电频率的函数，可用卡松经验公式计算：re＝π2f×10－4＝9.87f×10－4Ω/km，当f＝50Hz时为De——地中虚拟导线的等值深度，，它也是大地电阻率ρe和频率f的函数，即Ds——aa导线的自几何均距。......
2023-06-15
-
直线特性阻抗继电器的工作原理和应用详细阅读
在重负荷线路中，为了防止保护误动，可以采用直线特性阻抗继电器。由多个直线围成的共同区域就变成了多边形特性阻抗继电器。其中四边形阻抗继电器广泛用于距离保护中的测量元件。图3-7直线与四边形特性阻抗继电器图直线特性阻抗继电器；四边形阻抗继电器1.电抗继电器直线特性阻抗继电器的动作特性如图3-7 所示，图中直线阴影侧为动作区。......
2023-06-24
-
序阻抗的概念的分析介绍，详细阅读
我们以一个静止的三相电路元件为例来说明序阻抗的概念。根据以上的分析，所谓元件的序阻抗，是指元件三相参数对称时，元件两端某一序的电压降与通过该元件同一序电流的比值，即Z1、Z2、Z0分别称为该元件的正序阻抗、负序阻抗和零序阻抗。电力系统每个元件的正、负、零序阻抗可能相同，也可能不同，视元件的结构而定。......
2023-06-15
-
单相式圆特性阻抗继电器的特点和优势详细阅读
在手合或重合于故障时可以采用此类继电器。苹果型与橄榄型方向阻抗继电器是圆特性方向阻抗继电器的变形，当两个相交的圆特性方向阻抗继电器动作区取并集(逻辑或)时为苹果型方向阻抗继电器，当取交集(逻辑与)时为橄榄型方向阻抗继电器。下抛圆特性阻抗继电器如图3-6 所示，是用于发电机失磁保护中的测量元件。......
2023-06-24
-
电波传播特性分析详细阅读
图10.2电波的反射直射波TR 的行程与反射波TPR 的行程差为Δr=r2-r1假设d h1，h2则所以设地面反射波的反射系数为ρ。图10.3电波传播的刃形阻挡图10.4路径余隙造成的阻挡效应如图10.5所示，满足的所有点Q 的集合叫第n 菲涅尔区。图10.5电波传播的菲涅尔区第n菲涅尔区边界上的某个点P 到T、R 连线的距离Fn叫第n 菲涅尔区半径。......
2023-06-26
-
热和电气特性分析与优化详细阅读
如前所述，大多数LED具有保护功能，避免在电压达10kV或20kV的直接或反向静电放电情况下受到损坏。从热的角度看，LED具有以下特性：1）结和热沉之间的热阻为Rj-s，目前LED的Rj-s一般在5～15K/W，而多芯片LED的热阻低于5K/W；2）正向电压温度系数的单位是V/℃；3）最大结温；4）额定工作模式下的环境空气温度的最大范围。在5.3节中已经解释过最后一个特性非常依赖于热阻Rj-s，但也依赖于总热阻Rj-a。......
2023-06-15
-
典型装甲目标的特性分析详细阅读
图4.1披挂ERA的主战坦克图4.2ERA抗弹防护原理目前，俄罗斯、美国、德国、英国、法国、以色列、中国等国均已发展了系列化ERA，其中又以俄罗斯“接触/K”系列ERA最具代表性。图4.6美国“福特”级航母结构布局现代大中型......
2023-06-18
相关推荐