我们以一个静止的三相电路元件为例来说明序阻抗的概念。根据以上的分析，所谓元件的序阻抗，是指元件三相参数对称时，元件两端某一序的电压降与通过该元件同一序电流的比值，即Z1、Z2、Z0分别称为该元件的正序阻抗、负序阻抗和零序阻抗。电力系统每个元件的正、负、零序阻抗可能相同，也可能不同，视元件的结构而定。......
2023-06-15
单导线大地回路的自阻抗和互阻抗分析
【摘要】：图11-14示出一“单导线－大地”回路。根据推导得，“单导线－大地”回路的自阻抗为上式中ra——单位长度导线aa的电阻；re——单位长度虚拟导线ee的等值电阻，它是所通交流电频率的函数，可用卡松经验公式计算：re＝π2f×10－4＝9.87f×10－4Ω/km，当f＝50Hz时为De——地中虚拟导线的等值深度，，它也是大地电阻率ρe和频率f的函数，即Ds——aa导线的自几何均距。
图11-14（a）示出一“单导线－大地”回路。导线aa与大地平行，导线中流过电流I.a，经由大地返回。设大地体积无限大，且具有均匀的电阻率，则地中电流就会流经一个很大的范围，这种“单导线－大地”的交流电路，可以用卡松（carson）线路来模拟，如图11-14（b）所示。卡松线路就是用一虚拟导线ee作为地中电流的返回导线。该虚拟导线位于架空线aa的下方，与aa的距离为Dae。
根据推导得，“单导线－大地”回路的自阻抗为
上式中 ra——单位长度导线aa的电阻；
re——单位长度虚拟导线ee的等值电阻，它是所通交流电频率的函数，可用卡松经验公式计算：re＝π2f×10－4＝9.87f×10－4Ω/km，当f＝50Hz时为
De——地中虚拟导线的等值深度，
（Dse为虚拟导线ee的自几何均距），它也是大地电阻率ρe和频率f的函数，即
Ds——aa导线的自几何均距。
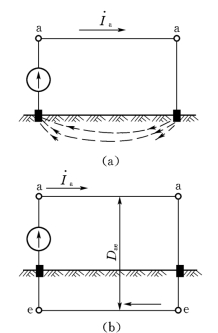
图11-14 “单导线—大地”回路
如果有两根平行长导线都以大地作为电流的返回路径，也可以用一根虚拟导线ee来代表地中电流的返回导线，这样就形成了两个平行的“单导线－大地”回路，如图11-15所示。记两导线轴线间的距离为D，两导线与虚拟导线间的距离分别为Dae和Dbe。两个回路之间单位长度的互阻抗Zm可以这样求得：当一个回路通以单位电流时，在另一个回路单位长度上产生的电压降，在数值上即等于Zm。因此，可推得
由于虚拟导线ee远离导线aa和bb，故有
上式可简写成
有关电力系统分析的文章
- 详细阅读
-
综合负荷的阻抗特性分析详细阅读
在上述两种情况以外的短路计算中，负荷的正序参数常用恒定阻抗表示，即图11-23确定电动机正序阻抗的等值电路式中SLD、ULD——负荷的视在功率和负荷节点的电压。异步电动机是旋转元件，其负序阻抗不等于正序阻抗。我们看到，异步电动机的负序阻抗也是转差的函数。计及降压变压器及馈电线路的电抗，则以异步电动机为主要成分的综合负荷的负序电抗为它是以综合负荷的视在功率和负荷接入点的平均额定电压为基准的标么值。......
2023-06-15
-
阻抗方程与Z参数简介详细阅读
式中的系数Z11、Z12、Z21、Z22具有阻抗性质，所以式称为阻抗方程或Z方程。由此得出即Z12是输入端口开路时的转移阻抗，称为开路转移阻抗。无源线性二端口网络如果同时满足式 时，则Z参数中只有两个参数是独立的。......
2023-06-24
-
求解线圈阻抗及复功率公式详细阅读
复功率的单位仍用。 如图4.15所示，把一个线圈接到f=50Hz的正弦电源上，分别用电压表、电流表、功率表测得电压U=50V、电流I=1A、功率P=30W，试求R、L之值，并求线圈吸收的复功率。解：根据三个电表的读数，可先求线圈阻抗图4.15[例4.8]电路图功率表的读数为线圈吸收的有功功率，则图4.15[例4.8]电路图功率表的读数为线圈吸收的有功功率，则还可以用另外一种方法，即还可以用另外一种方法，即......
2023-06-24
-
架空地线对输电线路零序阻抗和等效电路的影响分详细阅读
图11-19有架空地线的输电线路及其零序等值电路由方程式可以解出其中这就是具有架空地线的三相输电线路每相的等值零序阻抗。利用式可以求得Zgm0的单位长度的值式中DL—g——线路和架空地线间的互几何均距，即式表明，架空地线使输电线路的等值零序阻抗减小。各导线间的距离为试计算输电线路的零序阻抗。两回线路间的互几何均距两线路间的零序互阻抗于是可得求计及架空地线及另一回线路影响后每一线路的零序阻抗Z′0。......
2023-06-15
-
单相式圆特性阻抗继电器的特点和优势详细阅读
在手合或重合于故障时可以采用此类继电器。苹果型与橄榄型方向阻抗继电器是圆特性方向阻抗继电器的变形，当两个相交的圆特性方向阻抗继电器动作区取并集(逻辑或)时为苹果型方向阻抗继电器，当取交集(逻辑与)时为橄榄型方向阻抗继电器。下抛圆特性阻抗继电器如图3-6 所示，是用于发电机失磁保护中的测量元件。......
2023-06-24
-
阻抗继电器精确工作电流的优化方案详细阅读
其中的最小值称为最小精确工作电流Iac.min；最大值称为最大精确工作电流Iac.max，最大精确工作电流取决取于保护使用的变换器抗饱和能力。测量阻抗继电器的精确工作电流方法是给继电器加不同的电流，测出使得继电器刚好动作的电压，电压与电流的比值就是起动阻抗Zact。作出曲线Zact=f，并取与直线Zop=0.9Zset的交点，对应的电流值就是精确工作电流如图3-8所示。......
2023-06-24
-
二、三相输电线路的零序阻抗值分析详细阅读
如图11-16所示为以大地为回路的三相输电线路，地中电流返回路径仍以一根虚拟导线表示。当输电线路通以零序电流时，在a相回路每单位长度上产生的电压降为图11-15两平行的“单导线—大地”回路图11-16以大地为回路的三相输电线路因此，三相线路每单位长度的一相等值零序阻抗为此式与式的结果相同。由于输电线路所经地段的大地电阻率一般是不均匀的，因此零序阻抗一般要通过实测才能得到较为准确的数值。......
2023-06-15
相关推荐