对称分量法在不对称短路计算中的应用

2025-09-29 历史故事版权反馈

【摘要】：现以图11-3所示简单电力系统为例来说明应用对称分量法计算不对称短路的一般原理。应用对称分量法将这组不对称电势源分解成正序、负序和零序三组对称分量，如图11-4所示。它说明了各种不对称短路时各序电流和同一序电压间的相互联系，表示了不对称短路的共性。根据不对称短路的类型可以得到三个说明短路性质的补充条件，它们表示了各种不对称短路的特性，通常称为故障条件或边界条件。

现以图11-3所示简单电力系统为例来说明应用对称分量法计算不对称短路的一般原理。一台发电机接于空载输电线路，发电机中性点经阻抗Zn接地。在线路某处发生单相（例如a相）短路，使故障点出现了不对称的情况。a相对地阻抗为零（不计电弧等电阻），a相对地电压而b、c两相的电压［见图11-4（a）］。此时，故障点以外的系统其余部分的参数（指阻抗）仍然是对称的。因此，在计算不对称短路时，应设法把故障点的不对称转化成对称，使被短路破坏了的对称性的三相电路转化成对称电路，然后就可以用单相电路进行计算。

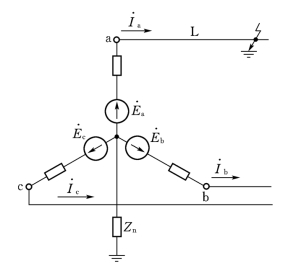
pagenumber_ebook=191,pagenumber_book=184

图11-3　简单电力系统的单相短路

短路点处的不对称电压为可用电势源表示，如图11-4（b）所示。应用对称分量法将这组不对称电势源分解成正序、负序和零序三组对称分量（各序具有独立性），如图11-4（c）所示。根据叠加原理，图11-4（c）所示的状态，可以当作是图11-4（d）、（e）、（f）三个图所示状态的叠加。

图11-4（d）的电路称为正序网络，其中只有正序电势在作用（包括发电机的电势和故障点的正序分量电势），网络中只有正序电流，各元件呈现的阻抗就是正序阻抗。图11-4（e）及（f）的电路分别称为负序网络和零序网络。因为发电机只产生正序电势，所以在负序和零序网络中，只有故障点的负序和零序分量电势在作用，网络中也只有同一序的电流，元件也只呈现同一序的阻抗。

根据这三个电路图，可以分别列出各序网络的电压方程式。因为每一序都是三相对称的，只需列出一相便可以了。在正序网络中，当以a相为基准相时，有

因为中性点接地阻抗Zn上的电压降为零，它在正序网络中不起作用。这样，正序网络的电压方程可写成

在负序网络中，由于而且发电机的负序电势为零，因此，负序网络的电压方程为

pagenumber_ebook=191,pagenumber_book=184

pagenumber_ebook=192,pagenumber_book=185

图11-4　对称分量法的应用

在零序网络中，由于在中性点接地阻抗中将流过三倍的零序电流，产生电压降。计及发电机的零序电势为零，零序网络的电压方程为

(https://www.chuimin.cn)

或写为

根据以上所得的各序电压方程式，可以绘出各序的等值网络（见图11-5）。必须注意，在一相的零序网络中，中性点接地阻抗必须增大为三倍。这是因为接地阻抗Zn上的电压降是由三倍的一相零序电流产生的，在数值上，它等于一相零序电流在三倍中性点接地阻抗上产生的电压降。

虽然实际的电力系统接线复杂，发电机的数目也很多，但是通过网络化简，仍然可以得到与以上相似的各序电压方程式

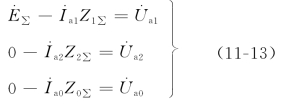
pagenumber_ebook=193,pagenumber_book=186

式中　——正序网络中相对短路点的戴维宁等值电势；

　　　Z1∑、Z2∑、Z0∑、——正序、负序和零序网络中短路点的输入阻抗；

　　　——短路点电流的正序，负序和零序分量；

pagenumber_ebook=193,pagenumber_book=186

图11-5　正序、负序和零序等值网络

（a）正序；（b）负序；（c）零序

　　　——短路点电压的正序，负序和零序分量。

方程式（11-13）又称为序网方程，它对各种不对称短路都适用。它说明了各种不对称短路时各序电流和同一序电压间的相互联系，表示了不对称短路的共性。根据不对称短路的类型可以得到三个说明短路性质的补充条件，它们表示了各种不对称短路的特性，通常称为故障条件或边界条件。例如，a相接地的故障条件为用各序对称分量表示可得

pagenumber_ebook=193,pagenumber_book=186

由式（11-13）和式（11-14）的六个方程，便可解出短路点电压和电流的各序对称分量。

对称分量法在不对称短路计算中的应用

相关推荐