图9-9暂态电势和暂态电抗的等值电路习惯上称E′q为暂态电势，它同励磁绕组的总磁链Ψf成正比。电势正比于磁链，由此可见，暂态电势E′q也是某种意义下的气隙电势，暂态电抗x′d则是某种意义下的定子漏抗。如果令便可将方程式改写成电势常称为暂态电抗后的电势。以上根据磁链平衡方程式导出了暂态电势和暂态电抗的表达式，并对这些参数的意义作了说明。暂态电势在运行状态发生突变瞬间能够守恒。......
2023-06-15
次暂态电势与电抗
【摘要】：图9-13次暂态电势E″q和次暂态电抗x″d的等值电路同样地，交轴方向的等值电路也可以作类似的简化［见图］。图中的E″d称为次暂态电势的直轴分量，x″q称为交轴次暂态电抗，这两个次暂态参数的表达式如下电势E″d同交轴阻尼绕组的总磁链φQ成正比，运行状态发生突变时，φQ不能突变，电势E″d也就不能突变。
对于有阻尼绕组电机，由式（8-19）的磁链平衡方程，可以做出等值电路如图9-12所示。
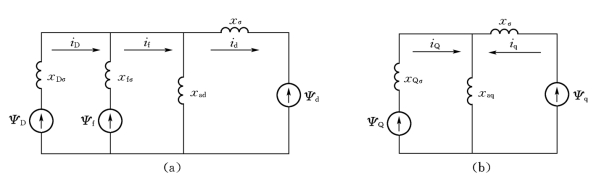
图9-12 有阻尼绕组电机磁链平衡的等值电路
（a）d轴方向；（b）q轴方向
直轴方向的等值电路又可简化为图9-13（a）所示的电路。应用戴维宁定理可以导出
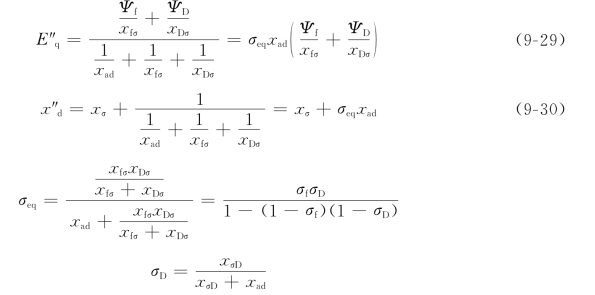
E″q称为次暂态电势交轴分量，它同励磁绕组的总磁链Ψf和直轴阻尼绕组的总磁链ΨD成线性关系。在运行状态突变瞬间Ψf和ΨD都不能突变，所以电势E″q也不能突变。x″d称为直轴次暂态电抗，如果沿同步电机直轴方向，把电机看做是三绕组变压器，次暂态电抗x″d就是这个变压器的两个副方绕组（即励磁绕组和直轴阻尼绕组）都短路时从原方（定子绕组侧）测得的电抗［见图9-13（b）］。σD是直轴阻尼绕组的漏磁系数。如果用一个等值绕组来代替励磁绕组和直轴阻尼绕组，σeq就是这个等值绕组的漏磁系数。
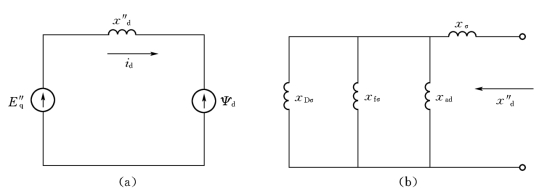
图9-13 次暂态电势E″q和次暂态电抗x″d的等值电路
同样地，交轴方向的等值电路也可以作类似的简化［见图（9-14）］。图中的E″d称为次暂态电势的直轴分量，x″q称为交轴次暂态电抗，这两个次暂态参数的表达式如下
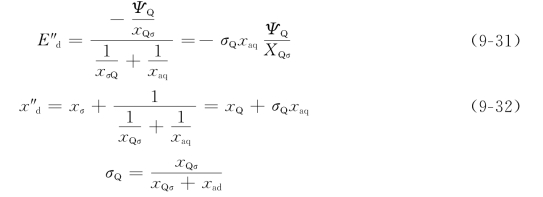
电势E″d同交轴阻尼绕组的总磁链φQ成正比，运行状态发生突变时，φQ不能突变，电势E″d也就不能突变。次暂态电抗x″q的等值电路示于图9-14（b）。称为交轴阻尼绕组的漏磁系数。
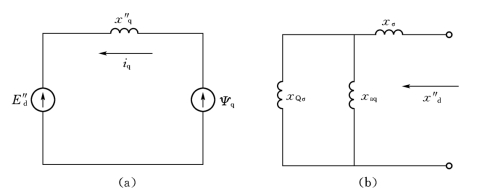
图9-14 次暂态电势E″d和次暂态电抗x″q的等值电路
引入次暂态电势和次暂态电抗以后，同步电机的磁链平衡方程可以改写为
当电机处于稳态或忽略变压器电势时，Ψd＝Uq，Ψq＝－Uq，便得定子电势方程如下
也可用交流相量的形式写成
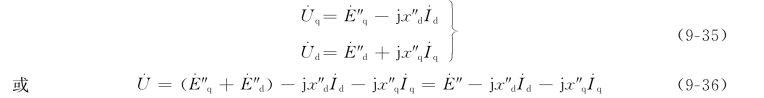
式中，
称为次暂态电势。电势相量图示于图9-15。
为了避免按两个轴向制作等值电路和列写方程，可采用等值隐极机的处理方法，将式（9-36）改写为
略去此式右端的第三项，便得
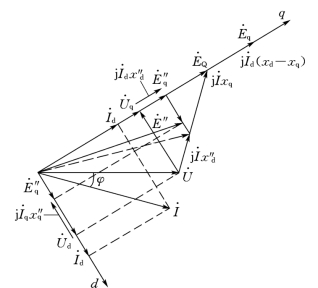
图9-15 同步电机相量图
这样确定的次暂态电势在图9-15中用虚线示出。由于x″d和x″q在数值上相差不大，由式（9-36）和式（9-37）确定的次暂态电势在数值上和相位上都相差很小。因此，在实用计算中，对于有阻尼绕组电机常根据式（9-37）做出等值电路见图（9-16），并认为其中的电势E″的数值是不能突变的。
还须指出，正如暂态参数一样，次暂态电抗x″d和x″q都是电机的实际参数，而次暂态电势E″d、E″q和E″则是虚拟的计算用参数。
【例9-2】同步发电机有如下的参数：
xd＝1.0，xq＝0.6，x′d＝0.3，x″d＝0.21，x″q＝0.31，cosφ＝0.85。试计算额定满载下Eq、E′q、E″q、E″d、E″。
解 本题电机参数除次暂态电抗外，都与例题9-1的电机的参数相同，可以直接利用例题8-2和例题9-1的下列计算结果：Eq＝1.73，E′q＝1.17，δ＝21.1°，Uq＝0.93，Ud＝0.36，Iq＝0.6，Id＝0.8。
根据上述数据可以继续算出
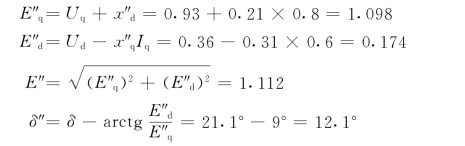
电势相量图示于图9-17
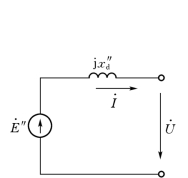
图9-16 简化的次暂态参数等值电路
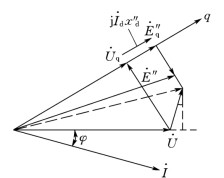
图9-17 例9-2的电势相量图
如果按近似公式（9-37）计算，由相量图9-15可知
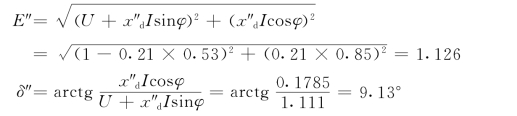
同前面的精确计算结果相比较，电势幅值相差甚小，相角误差略大。
我们已经导出了分别用稳态、暂态和次暂态参数列写的同步电机定子电势方程式，根据这些方程式可以做出相应的等值电路。各种不同的电势方程式（或相应的等值电路）都可用于稳态或暂态分析，并在工程计算中得到了实际的应用。但须注意，在每种电势方程（或相应的等值电路）中所用的电势同电抗间具有明确的对应关系，切不可混淆。
有关电力系统分析的文章
- 详细阅读
-
产业演变：三次大分工与三次革命详细阅读
到目前为止，产业的发展演变经历了三次社会大分工和三次产业革命。蒸汽机械化逐步被电力机械化所取代，电力、化工、汽车、石油、飞机、电讯等新兴产业得到迅猛发展，人类进入电气化、石油化、钢铁化的新阶段，再次使产业格局发生根本性的变革。......
2023-11-27
-
解析二次电路与一次电路的关系详细阅读
发电厂、变配电所的电气线路包括一次电路和二次电路：一次电路是指高电压、大电流电能流经的电路；二次电路是控制、保护、测量和监视一次电路的电路，二次电路一般通过电压互感器和电流互感器与一次电路建立电气联系的。图8-13是一次电路与二次电路的关系图。......
2023-06-15
-
用电势表示的功率特性详细阅读
1．用q轴电势Eq、E′q、UGq表示的功率特性由凸极发电机供电的简单电力系统的相量图如图13-19所示。应用相量图可求出用电势和功角表示的Id，即将式中的Iq及式中的Id代入式中，经整理后可得图13-19凸极发电机供电的简单电力系统相量图这些算式与一样，都包含磁阻功率项，而且当电势、电压均为常数时，功率与功角δ成非正弦的关系。应用上述公式计算功率特性时，须要根据给定的运行条件去确定E′q0、UGq0的值。......
2023-06-15
-
电路暂态分析技巧详解详细阅读
所谓 “控制”，实质上就是一个寻找各种期望的稳态值和缩短暂态时间，并减少暂态过程中出现危害的过程。“暂态”相对于“稳态”而言。电路的暂态过程实际上非常复杂，但在电路分析理论中研究它时，仅仅是对暂态过程中普遍遵循的最简单、最基本的规律进行研究和探讨，目的是让学习者建立起关于暂态的概念，并在认识“暂态”的过程中充分理解暂态过程中的三要素。......
2023-06-24
-
宴会座次安排与桌次策划详细阅读
(一)桌次排列中餐宴会活动的桌次安排有严格的礼仪规范和讲究。桌次的安排要根据宴会厅的形状和桌数的多少来确定。两桌组成的小型宴会,餐桌的排列,有时需要横排,有时则需要竖排。多桌宴会,应将排列序号放在餐桌上。安排就餐人数一般应限制在10人之内,并且以双数为好。主宾携夫人,而主人的夫人因故不能出席时,可请与主人有联系且身份相当的女士作第二主人；若无适当的女士出席,可把主宾夫妇安排在主人的左右两侧。......
2023-07-03
-
如何安装平波电抗器详细阅读
4）平波电抗器是直流滤波回路的组成部分，其电感值应与直流滤波器的参数统筹考虑，电感值大，则要求的直流滤波器规模小，反之亦然。因此，平波电抗器电感量的取值应与直流滤波器综合考虑，并进行费用的优化。......
2023-06-23
-
如何选择合适的电抗器？详细阅读
而接在变频器输出端和电动机之间的输出电抗器，其主要作用则是为了降低电动机的运行噪声。虽然输入电抗器容量的选择和电源容量有较大关系，但在一般情况下，可以按照在额定电压和额定电流条件使电抗器上的电压降低2%～5%之间的原则进行选择。当这些现象出现时，应该选用输出电抗器使变频器的输出平滑，以减小输出谐波产生的不良影响。常用直流电抗器的规格见表3-2。......
2023-06-19
相关推荐