重载型自动扶梯在国内外的公共交通建设中得到广泛使用，目的是希望自动扶梯能适应地铁等大客流公共交通场所恶劣的使用环境。可见美国的公共交通运输系统采用重载型自动扶梯的目的与我们是相同的。伦敦地铁是最早采用重载型自动扶梯的地铁，也是对自动扶梯的使用有深刻认识的地铁企业。自动扶梯经受了大客流、强载荷的使用考验。城市轨道交通的大规模发展，对重载型自动扶梯必然出现更大的需求。......
2025-09-29
暂态电势与电抗的分析与应用
【摘要】：图9-9暂态电势和暂态电抗的等值电路习惯上称E′q为暂态电势，它同励磁绕组的总磁链Ψf成正比。电势正比于磁链，由此可见，暂态电势E′q也是某种意义下的气隙电势，暂态电抗x′d则是某种意义下的定子漏抗。如果令便可将方程式改写成电势常称为暂态电抗后的电势。以上根据磁链平衡方程式导出了暂态电势和暂态电抗的表达式，并对这些参数的意义作了说明。暂态电势在运行状态发生突变瞬间能够守恒。
在电力系统分析中，常用等值电路来代表系统的各种元件，以便把某些待研究的问题归结为对电路的求解。对突然短路的计算分析也是这样。在图8-9所示的等值电路中，电势、电压和电流都是指基频分量，这种电路主要适用于稳态分析。在突然短路暂态过程中，定子和转子绕组都要出现多种电流分量，稳态等值电路显然不能适应这种复杂情况，即使是仅考虑定子方面的基频分量和转子方面的直流分量，由于其中包含有待求的自由分量，故稳态等值电路也不便应用。因此，必须制订更适合于暂态分析的等值电路。
暂态分析是以磁链守恒原则为基础的。可以设想，依据磁链平衡关系制订的等值电路将能适应暂态分析的需要。
根据方程组8-20，无阻尼绕组电机的磁链平衡方程如下
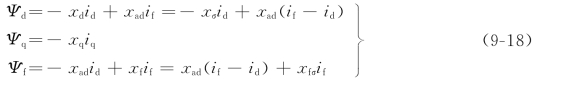
与方程式（9-18）相适应的等值电路示于图9-8。
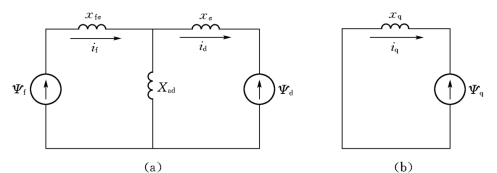
图9-8 无阻尼绕组电机的磁链平衡等值电路
（a）d轴方向；（b）q轴方向
如果从Ψd和Ψf的方程中消去励磁绕组电流if，又可得到
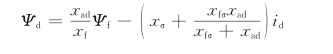
定义
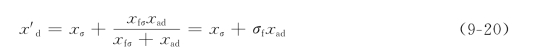
其中
是励磁绕组的漏磁系数。
这样，便得到下列方程
与方程式（9-21）相适应的等值电路示于图9-9（a）。
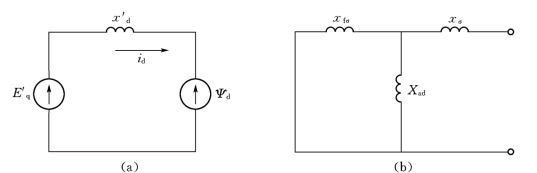
图9-9 暂态电势和暂态电抗的等值电路
习惯上称E′q为暂态电势，它同励磁绕组的总磁链Ψf成正比。运行状态突变瞬间，励磁绕组磁链守恒，Ψf不能突变，暂态电势E′q也就能突变。x′d称为暂态电抗，如果沿d轴方向把同步电机看做是双绕组变压器，当副方绕组（即励磁绕组）短路时，从原方（即定子绕组）测得的电抗即是x′d，其等值电路示于图9-9（b）。
现在我们对暂态电势和暂态电抗的物理意义再作一些说明。由方程式（9-18）的第一式，定子磁链的d轴分量可写成
上式右端的第一项代表电枢反应磁链与励磁绕组电流产生的有用磁链共同组成的气隙磁链Ψδd，第二项即是定子绕组的漏磁链Ψσ。
如果把电枢反应磁链作如下的分解，即
把电枢反应磁链的一部分（1－σf）xadid与励磁绕组电流产生的有用磁链合起来组成新的气隙磁链Ψ′δd，而把另一部分σfxadid与漏磁链合并为新的定子漏磁链Ψ′σ，便可得到
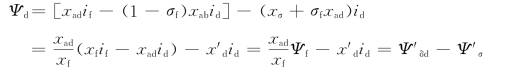
容易看出，这就是方程式（9-21）。电势正比于磁链，由此可见，暂态电势E′q也是某种意义下的气隙电势，暂态电抗x′d则是某种意义下的定子漏抗。由于0＜σf＜1，故知xσ＜x′d＜xd。如果励磁绕组没有漏磁，即σf＝0，便有Ψ′δd＝Ψδd和Ψ′σ＝Ψσ，暂态电势E′q就是普通意义下的气隙电势，x′d就是定子漏抗。因此，可以说，E′q和x′d是励磁绕组的漏磁效应以某种方式转移到定子方面时的一种等值的气隙电势和定子漏抗。(https://www.chuimin.cn)
当变压器电势Ψ.d＝Ψ.q＝0时，由于Ψd＝Uq和Ψq＝－Ud，定子磁链平衡方程便变为定子电势方程
这组方程既适用于稳态分析，也适用于暂态分析中将变压器电势略去或另作处理的场合。或者说，方程组（9-22）反映了定子方面电势、电压和电流的基频分量之间的关系。所以这组用暂态参数表示的电势方程式也可以写成交流相量的形式
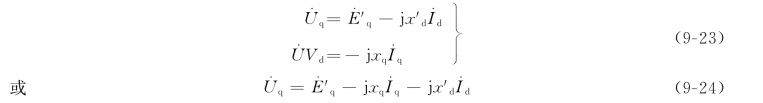
无论是凸极机还是隐极机，一般都有x′d≠xq。为便于工程计算，也常采用等值隐极机法进行处理。具体说又有以下两种不同的方案。
（1）用电势
和电抗Xq作等值电路。这时假想电势
将表示为
或者用绝对值表示时
由于xq＞x′d，故EQ＞E′q。
（2）用电势
和电抗
作等值电路。如果令
便可将方程式（9-24）改写成
电势
常称为暂态电抗后的电势。这个电势没有什么物理意义，纯粹是虚构的计算用电势，它的相位落后于暂态电势
在不要求精确计算的场合，常认为E′q守恒即是E′守恒，并且用E′的相位代替转子q轴的方向。这是一种不太精确的处理方法，但是颇有实用价值。
采用暂态参数时，同步电机的相量图示于图9-10。
以上根据磁链平衡方程式导出了暂态电势和暂态电抗的表达式，并对这些参数的意义作了说明。暂态电抗是同步电机的结构参数，可以根据设计资料计算出来，也可以进行实测，因此是实在的参数。暂态电势属于运行参数，它只能根据给定的运行状态（稳态或暂态）计算出来，但无法进行实测。暂态电势在运行状态发生突变瞬间能够守恒。利用这一特点，可以从突变前瞬间的稳态中算出它的数值，并且直接应用于突变后瞬间的计算中，从而给暂态分析带来极大的方便。但是必须指出，尽管能对暂态电势作出某些物理解释，它仍是虚构的、为方便计算而引用的参数。
【例9-1】就例8-2的同步机及所给运行条件，再给出x′d＝0.3，试计算电势E′q和E′。
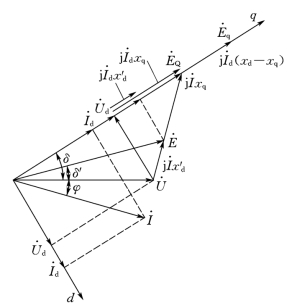
图9-10 同步电机的相量图
解 例8-2中已算出EQ＝1.45和Id＝0.81，因此
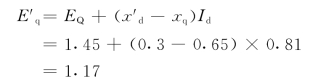
根据相量图9-11，可知
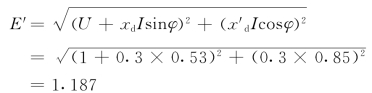
电势
同机端电压
的相位差为
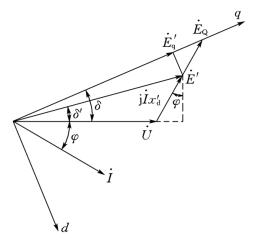
图9-11 例9-1的电势相量图
相关文章
- 详细阅读
-
轴承润滑方式与应用举例详细阅读
按润滑方式大体分为自润滑轴承和外注润滑脂润滑轴承两种。这种轴承能长期保持自润滑性能，在自动扶梯上得到广泛地使用。图9-1-9 自润滑密封轴承使用实例示意图a）滑动轴承 b）小链轮也有的普通型自动扶梯在不重要部位以自润滑滑动轴承代替滚动轴承，以降低生产成本。这种轴承的材料一般采用具有低摩擦因数的材料（如尼龙），有的带有一定的自润滑功能，在使用中也不需要加油。......
2025-09-29
-
电力线路的等值电路理论与应用详细阅读
当x＝0时，和由式和式可得由此可以解出将A1和A2代入式和式便得上式可利用双曲线函数写成当x＝l时，可得到线路首端电压和电流与线路末端电压和电流的关系如下将上述方程同二端口网络的通用方程相比较，若取和输电线就是对称的无源二端口网络，并可用对称的等值电路来表示。由于复数双曲线函数的计算很不方便，需要做一些简化。......
2025-09-29
- 详细阅读
-
智能动感单车的应用价值分析详细阅读
（二）国民的身体健康的监测和提高我国人民的身体素质与其身体的健康是我国是否可以维持久安长治的一个根本。当前所拥有的我国的国民身体素质监测系统在某种水平上来说，已经完成了对于国民身体素质的数值信息的收集与上报，但缺少了对于国民的身体素质的长久高效率的监控与督促，还有指导的后续服务形式。......
2025-09-29
- 详细阅读
-
变压器Π型等值电路的原理与应用详细阅读
为此，可以在变压器等值电路中增添只反映变比的理想变压器。双绕组变压器的这种等值电路示于图2-4中。变压器的Π型等值电路中三个阻抗（导纳）都与变比k有关，Π型的两个并联支路的阻抗（导纳）的符号总是相反的。与双绕组变压器一样，可以做出电气上直接相连的三绕组变压器等值电路，如图2-6所示。图2-6三绕组变压器的等值电路变压器采用Π型等值电路后，电力系统中与变压器相接的各元件就可以直接应用其参数的实际值。......
2025-09-29
-
功率方程的展开与平衡关系分析详细阅读
参照式（4-1），将展开可得功率方程的一般形式为1.功率方程的展开式以下面两端供电网络为例，分析功率方程的展开式。将式的第一、二式相加，第三、四式相加，可得这个系统的有功功率、无功功率平衡关系为两等式右边第三项、第四项为系统的有功功率损耗ΔP、无功功率损耗ΔQ在功率方程中，母线电压的相位角以δ12＝δ1－δ2的形式出现，即决定功率大小的是相对角而不是绝对角，因此在所有电压相量U.i中，应选定一个电压参考相量。......
2025-09-29
相关推荐