无限大功率电源供电电路的三相短路暂态过程

2025-09-29 历史故事版权反馈

【摘要】：图9-1是一个由无限大功率电源供电的简单三相电路，短路前处于正常稳态，由于电路对称，可以用对一相的讨论代替三相。当电路在f点发生突然三相短路，网络被短路点分成两个相互独立的部分，短路点左侧的部分仍与电源连接，右边的部分则被短接为无源网络。因此，三相电路的暂态过程主要针对短路点左侧的有源电路。

图9-1是一个由无限大功率电源供电的简单三相电路，短路前处于正常稳态，由于电路对称，可以用对一相的讨论代替三相。

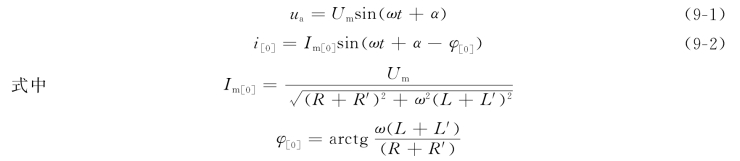
pagenumber_ebook=153,pagenumber_book=146

当电路在f点发生突然三相短路，网络被短路点分成两个相互独立的部分，短路点左侧的部分仍与电源连接，右边的部分则被短接为无源网络。在此无源网络中，短路前的电流为i［0］，该电路的暂态过程即是电流从这个初始值按指数规律衰减到零的过程，在此过程中，电路中储存的能量将全部转换成为电阻所消耗的热能。因此，三相电路的暂态过程主要针对短路点左侧的有源电路。

假设短路在t＝0s时发生，由于电路仍为对称，可以只研究其中的一相，例如a相，其电流的瞬时值应满足如下微分方程

这是一个一阶常系数，线性非齐次的常微分方程，它的特解即为稳态短路电流i∞a，又称交流分量或周期分量ipa为

pagenumber_ebook=154,pagenumber_book=147

式中　Z——短路回路每相阻抗（R＋jωL）的模值；

　　　φ——稳态短路电流和电源电压间的相角

　　　Im——稳态短路电流的幅值。

短路电流的自由分量衰减时间常数Ta为微分方程式（9-3）的特征根的负倒数，即

短路电流的自由分量电流为

又称为直流分量或非周期分量，它是不断减小的直流电流，其减小的速度与电路中L/R值有关。式中C为积分常数，其值即为直流分量的起始值。

短路的全电流为

式中的积分常数C可由初始条件决定。在含有电感的电路中，根据楞次定律，通过电感的电流是不能突变的，即短路前一瞬间的电流值（用下标［0］表示）必须与短路发生后一瞬间的电流值（用下标0表示）相等，即(https://www.chuimin.cn)

所以

将式（9-8）代入式（9-7）中便得

由于三相电路对称，只要用（α－120°）和（α＋120°）代替式（9-9）中的α就可分别得到b相和c相电流表达式。现将三相短路电流表达式综合如下：

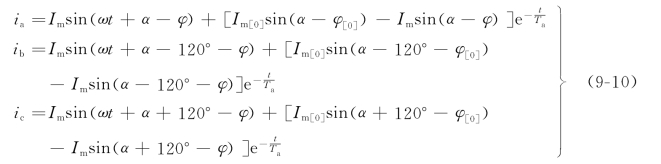
pagenumber_ebook=154,pagenumber_book=147

由上可见，短路至稳态时，三相中的稳态短路电流为三个幅值相等、相角相差120°的交流电流，其幅值大小取决于电源电压幅值和短路回路的总阻抗。从短路发生到短路稳态之间的暂态过程中，每相电流还包含有逐渐衰减的直流电流，它们出现的物理原因是电感中电流在突然短路瞬时的前后不能突变。很明显，三相的直流电流是不相等的。

图9-2示出三相电流变化的情况（在某一初相角α时）。由图可见，短路前三相电流和短路后三相的交流分量均为幅值相等、相角相差120°的三个正弦电流，直流分量电流使t＝0时短路电流值与短路前瞬间的电流值相等。由于有了直流分量，短路电流曲线便不与时间轴对称，而直流分量曲线本身就是短路电流曲线的对称轴。因此，当已知一短路电流曲线时，可以应用这个性质把直流分量从短路电流曲线中分离出来，即将短路电流曲线的两根包络线间的垂直线等分，如图9-2中ic所示。

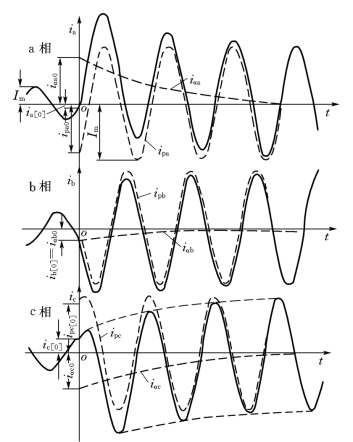
pagenumber_ebook=155,pagenumber_book=148

图9-2　三相短路电流波形图

由图9-2还可以看出，直流分量起始值越大，短路电流瞬时值越大。在电源电压幅值和短路回路阻抗恒定的情况下，由式（9-10）可知，直流分量的起始值与电源电压的初始相角α（相当于在α时刻发生短路）、短路前回路中的电流值有关。在图9-3（a）中画出了t＝0时a相的电源电压、短路前的电流和短路电流交流分量的相量图。显然，在时间轴上的投影分别为ia［0］和ipa0，它们的差值即为iαa0。如果改变α使相量差与时间轴平行，则a相直流分量起始值的绝对值最大；如果改变α使相量差与时间轴垂直，则a相直流电流为零，这时a相电流由短路前的稳态电流直接变为短路后的稳态电流，而不经过暂态过程。