一般采用F级绝缘、IP54外壳保护等级。各品牌对公共交通型自动扶梯的动力配置不尽相同，但一般以80%左右的制动载荷作为额定载荷计算电动机功率，通常比普通自动扶梯高20%以上。减速箱 普通自动扶梯多采用造价较低的单级蜗轮蜗杆减速箱。常采用的有全齿轮减速箱、一级齿轮一级蜗轮的减速箱。减速箱的工作寿命设计应不小于140000h。梯级链条的安全系数应不小于5。一般要求在制动载荷条件下，销轴比压不大于25N/mm2。......
2025-09-29
坐标变换与d、q、0系统
【摘要】：在原始方程中，定子各电磁变量是按三个相绕组也就是对于空间静止不动的三相坐标系统列写的，而转子各绕组的电磁变量则是对于随转子一起旋转的d、q两相坐标系统列写的。设发电机转子转速为ω，三相电流的瞬时值为试计算经派克变换后的id、iq、i0。则有由本例题可见，用a、b、c坐标系统和用d、q、0坐标系统表示的电流是交、直流互换的，这是一个重要的概念。
在原始方程中，定子各电磁变量是按三个相绕组也就是对于空间静止不动的三相坐标系统列写的，而转子各绕组的电磁变量则是对于随转子一起旋转的d、q两相坐标系统列写的。磁链方程式中出现变系数的原因主要是：
（1）转子的旋转使定、转子绕组间产生相对运动，致使定、转子绕组间的互感系数发生相应的周期性变化。
（2）转子在磁路上只是分别对于d轴和q轴对称而不是随意对称的，转子的旋转也导致定子各绕组的自感和互感的周期性变化。
图8-6 定子电流通用相量
在电机学中为了分析凸极电机中电枢磁势对旋转磁场的作用，一般采用双反应理论把电枢磁势分解为直轴分量和交轴分量。电机在转子的直轴方向和交轴方向磁路的磁阻都是完全确定的，这就避免了在同步电机的稳态分析中出现变参数的问题。
同步电机稳态对称运行时，电枢磁势幅值不变，转速恒定，对于转子相对静止。它可以用一个以同步转速旋转的矢量F.来表示。如果定子电流用一个同步旋转的通用相量I.m表示（它对于定子各相绕组轴线的投影即是各相电流的瞬时值），那么相量I.m与矢量F.在任何时刻都同相位，而且在数值上成比例，如图8-6所示。
依照电枢磁势的分解方法，也可以把电流相量分解为直轴分量id和交轴分量iq。令γ表示电流通用相量同a相绕组轴线的夹角，则有
定子三相电流的瞬时值则为
利用三角恒等式
即可从式（8-8）和式（8-9）得到
通过这种变换，将三相电流ia、ib、ic变换成了等效的两相电流id和iq。可以设想，这两个电流是定子的两个等效绕组dd和qq中的电流。这组等效的定子绕组dd和qq不像实际的a、b、c三相绕组那样在空间静止不动，而是随着转子一起旋转。等效绕组中的电流产生的磁势对转子相对静止，它所遇到的磁路磁阻恒定不变，相应的电感系数也就变为常数了。
当定子绕组内存在幅值恒定的三相对称电流时，由式（8-10）确定的id和iq都是常数。这就是说，等效的dd、qq绕组的电流是直流电流。
如果定子绕组中存在三相不对称的电流，只要是一个平衡的三相系统，即满足
仍然可以用一个通用相量来代表三相电流，不过这时通用相量的幅值和转速都不是恒定的，因而它在d轴和q轴上的投影也是幅值变化的。
当定子三相电流构成不平衡系统时，三相电流是三个独立的变量，仅用两个新变量（d轴分量和q轴分量）不足以代表原来的三个变量。为此，需要增选第三个新变量i0其值为(https://www.chuimin.cn)
式（8-11）与常见的对称分量法中零序电流的表达式相似。所不同的是，这里用的是电流的瞬时值，对称分量法中用的则是正弦电流的相量。我们称i0为定子电流的零轴分量。
式（8-10）和式（8-11）构成了一个从a、b、c坐标系统到d、q、0坐标系统的变换，可用矩阵合写成
或简记为
式中
为变换矩阵，容易验证，矩阵P非奇，因此存在逆阵P－1，即
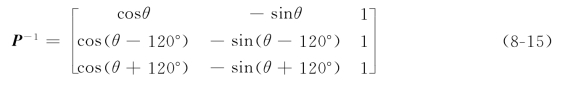
利用逆变换可得
或展开写成
由此可见，当三相电流不平衡时，每相电流中都含有相同的零轴分量i0。由于定子三相绕组完全对称，在空间互相位移120°电角度，三相零轴电流在气隙中的合成磁势为零，故不产生与转子绕组相交链的磁通。它只产生与定子绕组交链的磁通，其值与转子的位置无关。
上述变换一般称为派克（Park）变换，不仅对定子电流，而且对定子绕组的电压和磁链都可以施行这种变换，变换关系式与电流的相同。
【例8-1】设发电机转子转速为ω，三相电流的瞬时值为
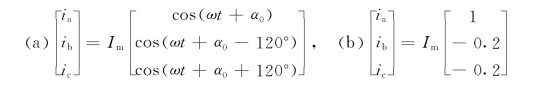
试计算经派克变换后的id、iq、i0。
解 d轴和a轴之间的夹角θ＝ωt＋θ0，θ0为t＝0时的夹角。则有
由本例题可见，用a、b、c坐标系统和用d、q、0坐标系统表示的电流是交、直流互换的，这是一个重要的概念。
相关文章
- 详细阅读
-
弹道测量系统的应用与发展详细阅读
从弹道修正火箭弹的基本工作原理可以看出, 弹道测量技术是进行弹道修正控制的基础, 为实现有效的弹道修正必须解决弹道测量的问题。采用该技术进行弹道修正火箭弹弹道参数测量时需要高附加值的地面设备, 且在整个过程中需要地面雷达持续的照射, 不利于武器系统的战场生存, 采用雷达进行弹道探测正在被淘汰。......
2025-09-29
-
弹道解算系统的应用与优势详细阅读
弹道解算技术是以弹道测量系统测量的弹道参数为初始量, 根据制导律要求解算出弹道偏差控制执行机构作用消除弹道偏差的过程, 是弹道修正弹研制过程中的另一关键技术。为了提高弹道预测解算的速度, 许多学者对弹道方程进行了线性化处......
2025-09-29
-
电器控制系统设计任务与内容简析详细阅读
电器控制系统设计的基本任务是：根据系统的控制要求，设计和编制出设备制造及使用维修过程中所必需的图样、资料，包括电气原理图、电气系统的组件划分与元器件布置图、安装接线图、电气箱图、控制面板及电器元件安装底板、非标准紧固件加工图等，编制外购成件目录、单台材料消耗清单、设备说明书等资料。......
2025-09-29
-
弹道测量技术：GPS测量系统详细阅读
GPS 整个卫星导航系统包括空间部分、地面支撑系统、用户设备三部分。图4-4弹载接收机组成图弹载接收机GPS 测量系统的特点是可对炮弹或火箭弹进行实时定位, 向地面发送定位信息所需的线路带宽较窄, 被测目标数量不受限制。弹载设备接收GPS 卫星L 波段信号, 经变频放大后, 通过遥测信道转发到地面,在地面完成对GPS 信号的测量和数据处理。地面设备包括GPS 接收设备和数据处理分系统。......
2025-09-29
-
弹道测量系统的应用与优势详细阅读
弹道测量系统的作用是采用不同的测量技术, 测量弹丸实际飞行过程中的位置及姿态信息、目标的位置或两者之间的相对运动信息, 为弹道解算提供数据。该探测方式下, 采用雷达设备对飞行的弹丸进行跟踪, 测量其速度、位置信息, 可获得高精度弹道信息, 但该方式不利于陆军战场的武器系统的战场生存。智能榴弹的末制导仍在研究过程中, 目前尚无研制完成的报道。......
2025-09-29
-
互联系统频率的调节方法详细阅读
大型电力系统的供电地区幅员宽广，电源和负荷的分布情况比较复杂，频率调整难免引起网络中潮流的重新分布。图6-7互联系统的功率交换图6-7表示系统A和B通过联络线组成互联系统。因此，对于系统A有对于系统B有互联系统应有相同的频率，故，ΔfA＝ΔfB＝Δf。当A、B两系统都进行二次调整，而且两系统的功率缺额又恰同其单位调节功率成比例，即满足条件时，联络线上的交换功率增量ΔPAB便等于零。这时，系统频率质量无法保证。......
2025-09-29
-
自动人行道安全保护系统设计与实现详细阅读
安全保护系统要保证自动人行道出现意外状况时，安全装置可有效地动作，制停自动人行道。各安全保护装置的确定，一般需根据安全电路的设计与评估原理，保证在不同的故障出现时，自动人行道均能有效地制停，保证乘客的安全。该安全保护装置一般安装在主驱动轴或踏板链位置附近，使用速度传感器或编码器检测踏板链的运行速度，当链条实际运行速度超出设定值时，监控装置会给控制系统发出信号使其切断电源，使自动人行道制停。......
2025-09-29
相关推荐