电感系数对定子绕组的影响

2023-06-15 历史故事版权反馈

【摘要】：1．定子各相绕组的自感系数以a相为例来讨论定子绕组自感系数的变化。2．定子各相绕组间的互感系数和自感系数的情况类似，凸极机的定子绕组互感也是随着转子转动呈周期性的变化，其周期也是π。以Mab为例讨论定子绕组间互感系数的变化。由于a、b两绕组在空间相差120°，a相绕组的正磁通交链到b相绕组总是负磁通，即定子绕组间的互感系数恒为负值。

1．定子各相绕组的自感系数

以a相为例来讨论定子绕组自感系数的变化。在图8-3（a）中画出了转子在四个不同位置时，a相绕组磁通所走的磁路。当θ为0°和180°时自感最大；当θ为90°和270°时自感最小。由此可知，a相自感的变化规律如图8-3（b）所示。Laa是θ角的周期函数，其变化周期为π，它还是θ角的偶函数，即转子轴在±θ的位置时，Laa的大小相等。

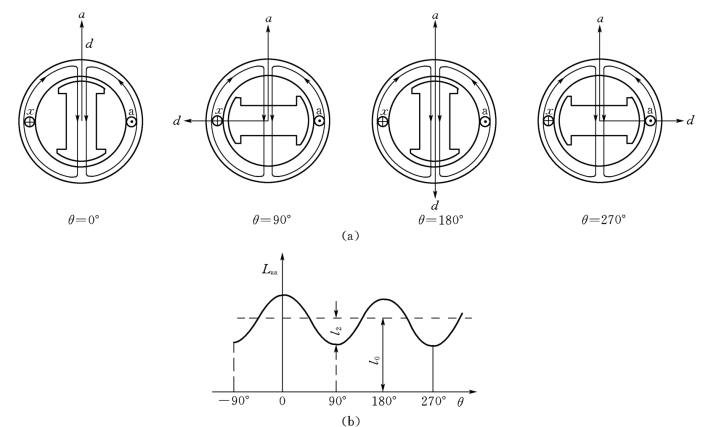
pagenumber_ebook=139,pagenumber_book=132

图8-3　定子绕组的自感

（a）不同位置的磁路图；（b）自感变化规律

周期性偶函数在分解为富氏级数时只含余弦项，而当函数变化周期为π时，只有偶次项，于是

根据正弦性的假设，略去其中4次及4次以上分量则

类似地，可得Lbb和Lcc的变化规律。定子各相绕组自感系数与θ角的函数关系可表示为

pagenumber_ebook=139,pagenumber_book=132

式中　l0——自感平均值；

　　　l2——自感变化部分的幅值。

由于自感总是正的，所以l0恒大于l2。隐极机的l2为零。

2．定子各相绕组间的互感系数

和自感系数的情况类似，凸极机的定子绕组互感也是随着转子转动呈周期性的变化，其周期也是π。以Mab为例讨论定子绕组间互感系数的变化。由于a、b两绕组在空间相差120°，a相绕组的正磁通交链到b相绕组总是负磁通，即定子绕组间的互感系数恒为负值。图8-4（a）示出转子在四个不同位置时a相交链b相的互磁通所走的路径。由图可见，当θ＝－30°和θ＝150°时，Mab的绝对值最大；θ＝60°和θ＝240°时，Mab的绝对值最小，变化周期为π。此外，由图8-4（a）还可见，如在滞后a相轴线30°处设一轴线，则当d轴超前或滞后这轴线相等角度时，a相和b相绕组间互感磁通路径上的磁导相同，Mab也相同，也就是说Mab是角θ＋30°的偶函数。图8-4（b）示出Mab随θ角的变化规律，与上述Laa情况相似，综上分析可列出定子各相绕组互感的表达式

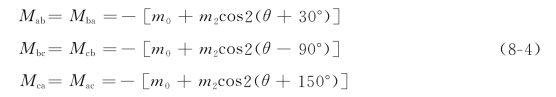
pagenumber_ebook=140,pagenumber_book=133

其中m0总大于m2。另外，根据理论分析和实验结果得知，互感变化部分的幅值与自感变化部分的幅值几乎相等，即m2≈l2。对于隐极机m2为零。

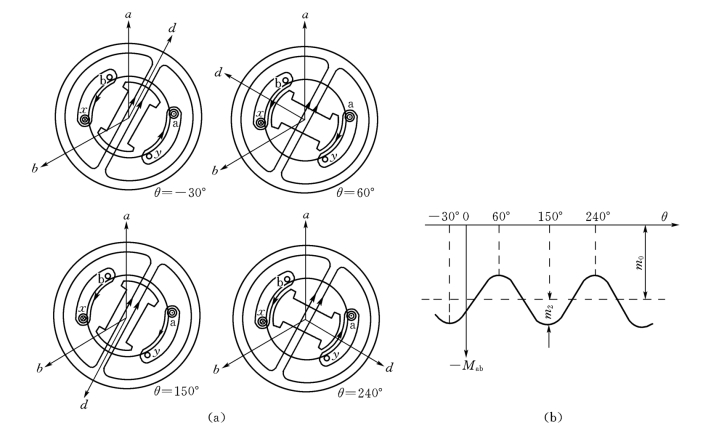
pagenumber_ebook=140,pagenumber_book=133

图8-4　定子绕组间的互感

（a）不同位置的磁路图；（b）互感变化规律

3．转子各绕组的自感系数

转子上各绕组是随着转子一起转的，无论是凸极机还是隐极机，转子绕组的磁路总是不变的，即转子各绕组的自感系数为常数，令它们表示为

4．转子各绕组间的互感系数

同于上述原因，它们也都是常数，而且Q绕组与f、D绕组互相垂直，它们的互感为零，即

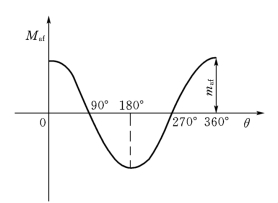
pagenumber_ebook=141,pagenumber_book=134

图8-5　Maf随θ角的变化曲线

5．定子绕组与转子绕组间的互感系数

无论是凸极机还是隐极机，这些互感显然与转子绕组相对于定子绕组的位置有关。以a相绕组与励磁绕组的互感系数Maf为例来讨论。当转子d轴与定子a相轴线重合时，即θ＝0°，两绕组间互感磁通路径的磁导最大，互感系数最大。转子旋转90°，θ＝90°，d轴与a相轴线垂直，而绕组间互感为零。转子再转90°，θ＝180°，d轴负方向与a相轴线正方向重合，互感系数为负的最大。Maf随θ角的变化如图8-5所示，其周期为2π。

定子各相绕组与励磁绕组间的互感系数与θ角的函数关系可表示如下式

pagenumber_ebook=141,pagenumber_book=134

定子绕组和直轴阻尼绕组间的互感系数与定子绕组和励磁绕组间的互感系数可类似表示为

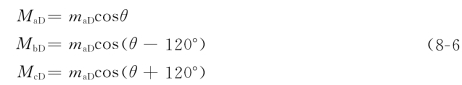
pagenumber_ebook=141,pagenumber_book=134

由于转子q轴超前于d轴90°，以（θ＋90°）替换式（8-6）中的θ，即可得定子绕组和交轴阻尼绕组间互感系数的表示式如下

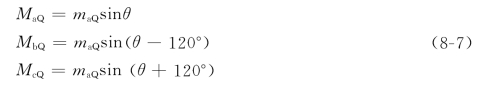
pagenumber_ebook=141,pagenumber_book=134

由以上分析可知，对于凸极机，大多数电感系数为周期性变化的，对于隐极机则小部分电感为周期性变化。无论是凸极机还是隐极机，如果将式（8-2）取导数后代入式（8-1）中，发电机的电势方程则是一组变系数的微分方程。用这种方程来分析发电机的运行状态是很困难的。为了方便起见，一般均用转换变量的方法，或者称为坐标变换的方法来进行分析。这种方法就是把a、b、c三个绕组的电流ia、ib、ic和电压ua、ub、uc以及磁链Ψa、Ψb、Ψc经过线性变换转换成另外三个电流、三个电压和三个磁链，或者说将a、b、c坐标系统上的量转换成另外一个坐标系统上的量。经过上述转换后，将上述方程式（8-1）和式（8-2）变成新变量的方程，这种新方程应便于求解。当然，在求得新的变量后可利用原线性变换关系来求得a、b、c三个绕组的量。目前已有多种坐标转换，这里只介绍其中最常用的一种，它是由美国工程师派克（Park）在1929年首先提出的（其后不久，原苏联学者戈列夫（ΓopeB）也独立地完成了大致相同的工作），一般称为派克变换。

电感系数对定子绕组的影响

相关推荐