当系统频率略有下降时,负荷的有功功率成正比例自动减小。图中直线的斜率为或用标么值表示图6-2负荷的有功功率—频率静态特性曲线KD、KD*称为负荷的频率调节效应系数或简称为负荷的频率调节效应。在实际系统中KD*=1~3,它表示频率变化1%时,负荷有功功率相应变化1%~3%。KD*的数值是调度部门必须掌握的一个数据,因为它是考虑按频率减负荷方案和低频率事故时用一次切除负荷来恢复频率的计算依据。......
2025-09-29
假定系统中只有一个水电厂和一个火电厂。水电厂运行的主要特点是,在指定的较短运行周期(一日、一周或一月)内总发电用水量W∑为给定值。水、火电厂间最优运行的目标是:在整个运行周期内满足用户的电力需求,合理分配水、火电厂的负荷,使总燃料(煤)耗量为最小。
用PT、F(PT)分别表示火电厂的功率和耗量特性;用PH、W(PH)分别表示水电厂功率和耗量特性。为简单起见,暂不考虑网损,且不计水头的变化。在此情况下,水、火电厂间负荷的经济分配问题可表述为:在满足功率和用水量两等式约束条件
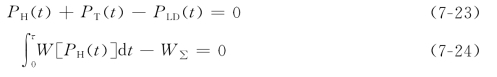
的情况下,使目标函数

为最小。
这是求泛函数极值的问题,一般应用变分法来解决。在一定的简化条件下也可以用拉格朗日乘数法进行处理。
把指定的运行周期τ划分为s个更短的时段
![]()
在任一时段Δtk内,假定负荷功率、水电厂和火电厂的功率不变,并分别记为PLD·k,PH·k和PT·k。这样,上述等式约束条件式(7-23)和式(7-24)将变为
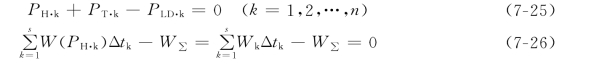
总共有s+1个等式约束条件。目标函数为
![]()
应用拉格朗日乘数法,为式(7-25)设置乘数λk(k=1,2,…,s),为式(7-26)设置乘数γ,构成拉格朗日函数
![]()
在式(7-27)的右端包含有PH·k、PT·k、λk(k=1,2,…,S)和γ共3s+1个变量。将拉格朗日函数分别对这3s+1个变量取偏导数,并令其为零,便得下列3s+1个方程
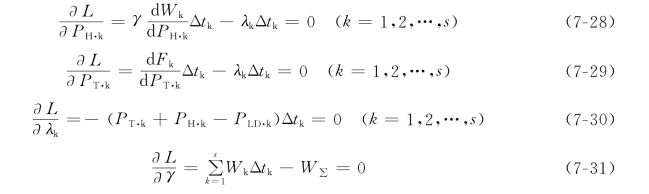
式(7-30)和式(7-31)就是原来的等值约束条件。式(7-28)和式(7-29)可以合写成
![]()
如果时间段取得足够短,则认为任何瞬间都必须满足

式(7-32)表明,在水、火电厂间负荷的经济分配也符合等微增率准则。
下面说明系数γ的物理意义。当火电厂增加功率ΔP时,煤耗增量为
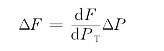
当水电厂增加功率ΔP时,耗水增量为
![]()
将两式相除并计及式(7-32)可得
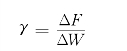
ΔF的单位是t/h,ΔW的单位为m3/h,因此,γ的单位为t(煤)/m3(水)。这就是说,按发出相同数量的电功率进行比较,1m3的水相当于γt煤。因此,γ又称为水煤换算系数。
把水电厂的水耗量乘以γ,相当于把水换成了煤,水电厂就变成了等值的火电厂。然后直接套用火电厂间负荷分配的等微增率准则,就可得到式(7-32)。
另一方面,若系统的负荷不变,让水电厂增发功率ΔP,则忽略网损时,火电厂就可以少发功率ΔP。这意味着用耗水增量ΔW来换取煤耗的节约ΔF。当在指定的运行周期内总耗水量给定,并且整个运行周期内γ值都相同时,煤耗的节约为最大。这也是等微增率准则的一种应用。水耗微增率特性可从耗水量特性求出,它与火电厂的微增率特性曲线相似。
按等微增率准则在水、火电厂间进行负荷分配时,需要适当选择γ的数值。一般情况下,γ值的大小与该水电厂给定的日用水量有关。在丰水期给定的日用水量较多,水电厂可以多带负荷,γ应取较小的值,因而根据式(7-32),水耗微增率就较大。由于水耗微增率特性曲线是上升曲线,较大的dW/dPH对应较大的发电量和用水量。反之,在枯水期给定的日用水量较少,水电厂应少带负荷。此时γ应取较大的值,使水耗微增率较小,从而对应较小的发电量和用水量。γ值的选取应使给定的水量在指定的运行期间正好全部用完。
对于上述简单情况,计算步骤大致为:(https://www.chuimin.cn)
(1)给定初值γ(0),这就相当于把水电厂折算成了等值火电厂。置迭代计数k=0。
(2)计算全部时段的负荷分配。
(3)校验总耗水量W(k)是否同给定值W∑相等,即判断是否满足
![]()
若满足则计算结束,否则做下一步计算。
(4)若W(k)>W∑,则说明γ(k)之值取得过小,应取γ(k+1)>γ(k);若W(k)<W∑,则说明γ(k)之值取得偏大,应取γ(k+1)<γ(k)。然后迭代计数1,返回第2步,继续计算。
【例7-3】一个火电厂和一个水电厂并联运行。火电厂的燃料消耗特性为
![]()
水电厂的耗量特性为
![]()
水电厂的给定日用水量为W∑=1.5×107m3。系统的日负荷变化如下:
0~8h负荷为350MW;8~18h负荷为700MW;18~24h负荷为500MW。火电厂容量为600MW,水电厂容量为450MW。试确定水、火电厂间的功率经济分配。
解 (1)由已知的水、火电厂耗量特性可得协调方程式
![]()
对于每一时段,有功功率平衡方程式为
![]()
由上述两方程可解出
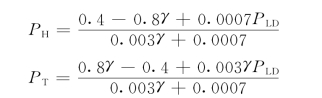
(2)任选γ的初始值,如取γ(0)=0.5,按已知各个时段的负荷功率值PLD1=350MW,PLD2=700MW和PLD3=500MW,即算出水火电厂在各时段应分担的负荷
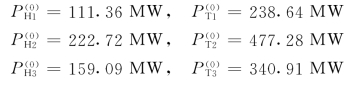
利用所求出的功率值和水电厂的水耗特性计算全日的发电耗水量,即
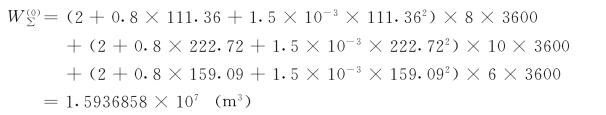
这个数值大于给定的日用水量,故宜增大γ值。
(3)取γ(1)=0.52,重做计算,求得
![]()
相应的日耗水量为
![]()
这个数值比给定用水量小,γ的取值应略为减小。若取γ(2)=0.514,可算出

继续做迭代,将计算结果列于表7-2。
表7-2

作四次迭代计算后,水电厂的日用水量已很接近给定值,计算到此结束。
相关文章

当系统频率略有下降时,负荷的有功功率成正比例自动减小。图中直线的斜率为或用标么值表示图6-2负荷的有功功率—频率静态特性曲线KD、KD*称为负荷的频率调节效应系数或简称为负荷的频率调节效应。在实际系统中KD*=1~3,它表示频率变化1%时,负荷有功功率相应变化1%~3%。KD*的数值是调度部门必须掌握的一个数据,因为它是考虑按频率减负荷方案和低频率事故时用一次切除负荷来恢复频率的计算依据。......
2025-09-29

电力系统运行中,所有发电厂发出的有功功率的总和PG,在任何时刻都是同系统的总负荷PD相平衡的。PD包括用户的有功负荷PLD∑、厂用电有功负荷PS∑以及网络的有功损耗PL,即为保证安全和优质供电,电力系统的有功功率平衡必须在额定运行参数下确立,而且还应具备一定的备用容量。旋转备用容量的作用在于及时抵偿由于随机事件引起的功率缺额。全部的旋转备用容量都承担频率调整任务。......
2025-09-29

1) 屏蔽屏蔽是抑制以场的形式造成干扰的有效方法。通常在程序的关键位置放置连续几个NOP 指令、LJMP 指令, 或者两者的组合, 将混乱或者跑飞的程序重新指向正确的位置, 如未使用的中断向量区、未使用的编程区、程序的转折区等。......
2025-09-29

图纸上的电气图布局是否合理,对能否正确、快速地识图有很大影响。电气图布局的原则是,便于绘制、易于识读、突出重点、均匀对称、清晰美观。在电气图布局时,可按以下步骤进行:1)明确电气图的绘制内容。电气图布局方向有水平布局和垂直布局,如图1-12所示。在水平布局时,应将元器件和设备在水平方向布置;在垂直布局时,应将元器件和设备在垂直方向布置。......
2025-09-29

梯级需要安装于梯级链轴上组成稳定的梯级联合体,在梯级链的牵引下,沿梯路导轨方向运行。因此,梯级与梯级链之间必须要有可靠的连接。但为了在日常维修中能方便地对梯级进行拆卸,梯级与梯级链之间的连接在结构上必须是相当简单的。但在套筒及梯级连接件中均加工有定位孔,并且在梯级连接件侧安装有定位弹簧销。......
2025-09-29

返回导轨与工作导轨不同,施加到导轨上的载荷几乎是固定的,梯级自重载荷Ws均等分布在4个梯级滚轮上,一个梯级距的梯级链重量的载荷Wc均匀分布在梯级主轮上。因返回主轮导轨和副轮导轨是分离设置的,下面以受力较大的主轮返回导轨为例讲解强度校核。要注意的是返回导轨的上曲线段与工作导轨上曲线段类似的法线张力,因此有必要对其进行强度和磨损分析,方法与工作导轨上曲线区段相同。......
2025-09-29

弹道导弹具有较强的修正能力, 弹道导弹的射击方向与发射装置和目标点之间的连线方向重合即可, 导弹飞行中控制系统将其严格控制在发射平面内直至命中目标。基于以上5 方面的原因, 无法将弹道摄动理论直接挪用到弹道修正火箭弹上。......
2025-09-29

从图5 -18 可看出, 微控制器功能主要包括感应装定功能、转数定距功能、自毁功能。图5-19某型引信专用处理器程序流程图在计转数定距模式, 程序首先配置计转数定距功能需要的片上资源测到预定状态, 然后取出装定数据并以此作为起始圈数对弹丸旋转圈数进行减计数,当装定圈数减到零时给出发火指令。......
2025-09-29
相关推荐