首页历史故事多发电厂负荷经济分配方案

多发电厂负荷经济分配方案

2023-06-15 历史故事版权反馈

【摘要】：拉格朗日函数L的无条件极值的必要条件为由于每个发电厂的燃料消耗只是该厂输出功率的函数，因此式又可写成这就是多个火电厂间负荷经济分配的等微增率准则。负荷经济分配中的不等式约束条件也与潮流计算的一样：任一发电厂的有功功率和无功功率都不应超出它的上、下限，即各节点的电压也必须维持在如下的变化范围内在计算发电厂间有功功率负荷经济分配时，这些不等式约束条件可以暂不考虑，待算出结果后再按式进行检验。

假定有n个火电厂，其燃料消耗特性分别为F1（PG1），F2（PG2），…，Fn（PGn），系统的总负荷为PLD，暂不考虑网络中的功率损耗，假定各个发电厂的输出功率不受限制，则系统负荷在n个发电厂间的经济分配问题可以表述为

在满足上式的条件下，使目标函数

pagenumber_ebook=129,pagenumber_book=122

图7-8　负荷在两台机组间的经济分配

为最小。

这是多元函数求条件极值问题。可以应用拉格朗日乘数法来求解。为此，先构造拉格朗日函数

其中λ称为拉格朗日乘数。

拉格朗日函数L的无条件极值的必要条件为

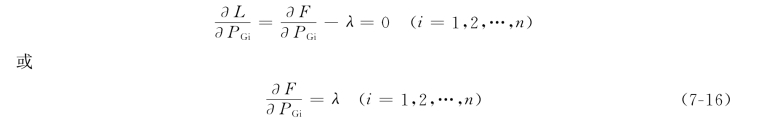
pagenumber_ebook=129,pagenumber_book=122

由于每个发电厂的燃料消耗只是该厂输出功率的函数，因此式（7-16）又可写成

这就是多个火电厂间负荷经济分配的等微增率准则。按这个条件决定的负荷分配是最经济的分配。

以上的讨论都没有涉及到不等式约束条件。负荷经济分配中的不等式约束条件也与潮流计算的一样：任一发电厂的有功功率和无功功率都不应超出它的上、下限，即

pagenumber_ebook=129,pagenumber_book=122

各节点的电压也必须维持在如下的变化范围内

在计算发电厂间有功功率负荷经济分配时，这些不等式约束条件可以暂不考虑，待算出结果后再按式（7-18）进行检验。对于有功功率值越限的发电厂，可按式（7-19）和式（7-20）条件留在有功负荷分配已基本确定以后的潮流计算中再进行处理。

【例7-2】三个火电厂并联运行，各电厂的燃料特性及功率约束条件如下

pagenumber_ebook=130,pagenumber_book=123

当总负荷为700MW和400MW时，试分别确定发电厂间功率的经济分配（不计网损的影响）。

解　（1）按所给耗量特性可得各厂的微增耗量特性为

pagenumber_ebook=130,pagenumber_book=123

令λ1＝λ2＝λ3，可解出

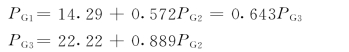
pagenumber_ebook=130,pagenumber_book=123

（2）总负荷为700MW，即PG1＋PG2＋PG3＝700。

将PG1和PG3都用PG2表示，便得

由此可计算出PG2＝270MW，已越出上限值，故应取PG2＝250MW。剩余的负荷功率450MW再由电厂1和电厂3进行经济分配。

将PG1用PG3表示，便得

由此解出PG3＝274MW和PG1＝450－274MW＝176MW，都在限值内。

（3）总负荷为400MW，即PG1＋PG2＋PG3＝400。

将PG1和PG3都用PG2表示，可得

于是，PG2＝147.7MW，PG1＝14.29＋0.572PG2＝14.29＋0.572×147.7MW＝98.77MW。

由于PG1已低于下限，故应取PG1＝100MW，剩余的负荷功率300MW，应在电厂2和电厂3之间重新分配。

将PG3用PG2表示，便得

由此可解出PG2＝147.05MW和PG3＝300－147.05MW＝152.95MW，都在限值内。