Kf是考虑交变电流趋肤效应和邻近效应对电阻的影响而引入的系数，即当导体中通过交变电流时，因趋肤效应和邻近效应而产生的附加损耗。则电阻损耗为式中：γ——材料的密度； m——材料的质量。电阻率ρ是温度θ的函数，其表达式为式中：ρ0、ρ20——0℃、200℃时的电阻率（Ω·m）； α、β——电阻温度系数。......
2023-06-30
线路能量损耗的计算方法
【摘要】：图7-1简单供电网如果线路中输送的功率一直保持为最大负荷功率Smax，在τh内的能量损耗恰等于线路全年的实际电能损耗，则称τ为最大负荷损耗时间。若认为电压接近于恒定，则由上式可见，最大负荷损耗时间τ与用视在功率表示的负荷曲线有关。试求线路及变压器中全年的电能损耗。对于已运行电网的能量损耗计算，此方法的误差太大，不宜采用。
这里简要介绍两种计算能量损耗的方法：最大负荷损耗时间法和等值功率法。
1.最大负荷损耗时间法
假定线路向一个集中负荷供电（见图7-1），在时间T内线路的电能损耗为
如果知道负荷曲线和功率因数，就可以做出电流（或视在功率）的变化曲线，并利用式（7-3）计算在时间T内的电能损耗。但是这种算法很繁。实际上，在计算电能损耗时，负荷曲线本身就是预计的，又不能确知每一时刻的功率因数，特别是在电网的设计阶段，所能得到的数据就更为粗略。因此，在工程实际中常采用一种简化的方法，即最大负荷损耗时间法来计算能量损耗。
图7-1 简单供电网
如果线路中输送的功率一直保持为最大负荷功率Smax，在τh内的能量损耗恰等于线路全年的实际电能损耗，则称τ为最大负荷损耗时间。
若认为电压接近于恒定，则
由上式可见，最大负荷损耗时间τ与用视在功率表示的负荷曲线有关。在一定的功率因数下视在功率与有功功率成正比，而有功功率负荷持续曲线的形状，在某种程度上可由最大负荷的利用小时Tmax反映出来。可以设想，对于给定的功率因数，τ同Tmax之间将存在一定的关系。通过对一些典型负荷曲线的分析，得到的τ和Tmax的关系列于表7-1。
表7-1 最大负荷损耗小时数τ与最大负荷的利用小时数Tmax的 关系
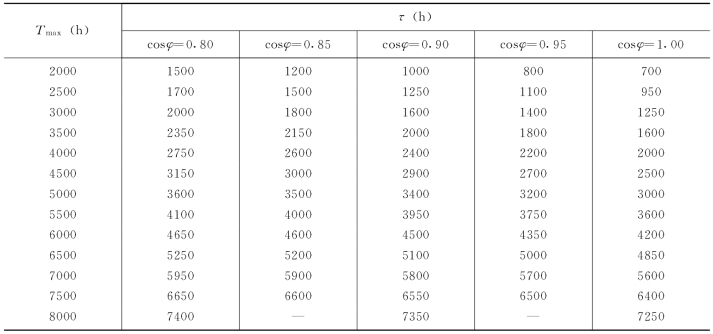
在不知道负荷曲线的情况下，根据最大负荷利用小时数Tmax和功率因数，即从表7-1中找出τ值，用以计算全年的电能损耗。
【例7-1】图7-2所示的网络，变电所低压母线上的最大负荷为40MW，cosφ＝0.8，Tmax＝4500h。试求线路及变压器中全年的电能损耗。线路和变压器的参数如下：
线路（每回）：r0＝0.17Ω/km，x0＝0.409Ω/km，b0＝2.82×10－6S/km
变压器（每台）：ΔP0＝86kW，ΔPS＝200kW，I0%＝2.7，US%＝10.5
解 最大负荷时变压器的绕组功率损耗
图7-2 例7-1的输电系统及其等值电路
变压器的铁芯功率损耗
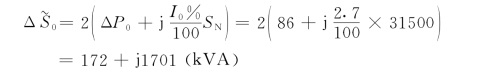
线路末端充电功率
等值电路中用以计算线路损失的功率
线路上的有功功率损失
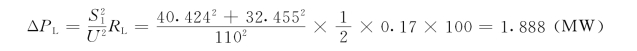
已知Tmax＝4500h和cosφ＝0.8，从表7-1中查得τ＝3150h，假定变压器全年投入运行，则变压器中全年能量损耗
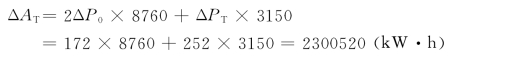
线路中全年能量损耗
输电系统全年的总能量损耗
用最大负荷损耗时间计算电能损耗，准确度不高，ΔPmax的计算，尤其是τ值的确定都是近似的，而且还不可能对由此而引起的误差做出有根据的分析。因此，这种方法只适用于电力网的规划设计中的计算。对于已运行电网的能量损耗计算，此方法的误差太大，不宜采用。
2.等值功率法
仍以图7-1的简单网络为例，在给定的时间T内的能量损耗
式中 Ieq、Peq、Qeq——电流，有功功率、无功功率的等效值。
当电网的电压恒定不变时，Peq与Qeq也有与式（7-7）相似的表达式。由此可见，所谓等效值实际上也是一种均方根。
电流有功功率和无功功率的等效值可以通过各自的平均值表示为
式中 G、K、L——负荷曲线I（t），P（t）、Q（t）的形状系数。
引入平均负荷后，可将电能损耗公式改写为
利用式（7-9）计算电能损耗时，平均功率可由给定运行时间T内的有功电量AP和无功电量AQ求得
形状系数K由负荷曲线的形状决定。对各种典型的持续负荷曲线的分析表明，形状系数的取值范围是
式中 a——最小负荷率。
当a＞0.4时，其最大可能的相对误差不会超过10%。当负荷曲线的最小负荷率a＜0.4时，可将曲线分段，使对每一段而言的最小负荷率大于0.4，这样就能保证总的最大误差在10%以内。
对于无功负荷曲线的形状系数L也可以作为类似的分析。当负荷的功率因数不变时，L与K相等。
用等值功率计算法计算电能损耗，原理易懂，方法简单，所要求的原始数据也不多。对于已运行的电网进行网损的理论分析时，可以直接从电能表取得有功电量和无功电量的数据，即使不知道具体的负荷曲线形状，也能对计算结果的最大可能误差做出估计。这种方法的另一个优点是能够推广应用于任意复杂网络的电能损耗计算。
有关电力系统分析的文章
- 详细阅读
-
电力线路中的电压降低与损耗问题详细阅读
在计算线路电压中，常用到电压降落、电压损耗、电压偏移、电压调整等几个指标，它们的定义如下：电压降落。指线路始末两端电压的向量差它的两个分量ΔU.和δU.分别称为电压降落的纵分量和横分量。电压偏移也常以线路额定电压UN百分数表示，即电压调整。由于输电线路的电容效应，特别是超高压线路，在空载时线路末端电压上升较大。......
2023-06-15
-
电动力计算方法：能量平衡法详细阅读
以安培力公式计算复杂回路中导体所受电动力殊为不便，有时甚至不可能。这时，可以使用基于磁场能量变化的能量平衡法。磁能对磁链的导数dWM/dψ=i/2。......
2023-06-30
-
太阳：巨大的能量源泉详细阅读
根据万有引力定律，在已知地球质量为6.0×1021t的情况下，可推算出太阳的质量为1.989×1027t，即太阳质量是地球质量的33万倍，等于太阳系所有行星质量总和的745倍。利用光谱分析法，已经初步探明了太阳的化学组成。构成太阳的主要成分是氢和氦。根据爱因斯坦相对论，通过热核反应，质量可以转化为能量。已知太阳的质量为1.989×1030kg，因而按照目前的太阳辐射水平，太阳上氢的含量足够维持800亿年。......
2023-06-23
-
太阳的能量及应用潜力详细阅读
太阳99%的能量就是由中心核反应区的热核反应产生的。图2-1太阳的构造太阳的内部主要可以分为三层：核心区、辐射区和对流区。到达陆地表面的太阳辐射能大约17×104亿kW，只占到达地球范围内太阳辐射能的1/10。即使如此，17×104亿kW的能量相当于全球一年内消耗总能量的3.5万倍，由此可见太阳能利用的巨大潜力。......
2023-07-02
-
光纤的传输损耗与损耗谱及侧向应力关系详细阅读
石英紫外吸收损耗和瑞利散射损耗是材料本身固有的，称为石英材料的本征损耗。光纤的传输损耗与工作波长密切相关，光纤的传输损耗与工作波长之间的关系称为光纤的损耗谱。如果光纤受到侧向应力的影响，则其损耗可能会相当大。......
2023-06-27
-
能量管理的有效策略详细阅读
能量管理策略是混合动力车辆控制系统的核心，也是混合动力车辆领域研究最为广泛和深入的内容。基于规则的能量管理策略通常依靠设计者的工程经验制定。基于优化的能量管理策略主要包含全局优化能量管理和实时优化能量管理两种。此后，文献［39-43］也提出了针对混合动力车辆的基于DP的能量管理策略。......
2023-06-24
-
铁磁材料的损耗及降低方法详细阅读
非载流铁磁质零部件在交变电磁场作用下产生的损耗，称为铁磁损耗，即铁耗PFe。同时磁通的方向和数值变化使铁磁材料反复磁化，产生磁滞损耗，涡流损耗与磁滞损耗导致包围载流导体的铁磁零件发热。减小铁磁损耗的常用措施有以下两种。采用非磁性间隙，若在磁通的路径中出现非磁性间隙，则磁阻加大，铁磁零件内磁通减小，因此损耗减小。......
2023-06-30
相关推荐