当电位梯度超过允许值时,可采用下列措施进行均压:采用方孔接地网。实例表明,方孔接地网是提高变电所接地网均压效果的有效措施。它是近年来我国发电厂、变电所接地网设计中所采用的一项新技术。综上所述,为保证接地网的安全运行,宜采用其接地电阻值和网格电压作为安全判据。为使地网电位分布均匀,避免发生由接地网不良引起的事故,设计接地网时应采用方孔接地网或不等间距接地技术,并严格保证施工质量。......
2023-06-27
如何进行电力系统频率的调整？
【摘要】：要确定电力系统的负荷变化引起的频率波动，需要同时考虑负荷及发电机组两者的调节效应，为简单起见先只考虑一台机组和一个负荷的情况。这就是说在频率为f1时达到了发电机组有功输出与系统的有功需求之间的平衡。正因为这样，依靠调速器进行的一次调整只能限制周期较短、幅度较小的负荷变动引起的频率偏移。负荷变动周期更长、幅度更大的调频任务自然地落到了二次调整方面。
要确定电力系统的负荷变化引起的频率波动，需要同时考虑负荷及发电机组两者的调节效应，为简单起见先只考虑一台机组和一个负荷的情况。负荷和发电机组的静态特性如图6-4所示。在原始运行状态下，负荷的功频特性为PD（f），它同发电机组静态特性的交点A确定了系统的频率为f1，发电机组的功率（也就是负荷功率）为P1。这就是说在频率为f1时达到了发电机组有功输出与系统的有功需求之间的平衡。
假定系统的负荷增加了ΔPD0，其特性曲线变为P′D（f）。发电机组仍是原来的特性。那么新的稳态运行点将由P′D（f）和发电机组的静态特性的交点B决定，与此相应的系统频率为f2。由图6-5可见，由于频率变化了Δf，且
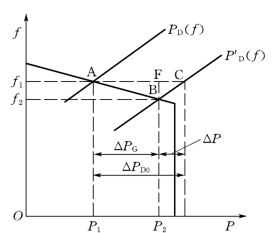
图6-5 电力系统功率—频率静态特性
发电机组的功率输出的增量
由于负荷的频率调节效应所产生的负荷功率变化为
当频率下降时，ΔPD是负的。故负荷功率的实际增量为
它应同发电机组的功率增量相平衡，即
或
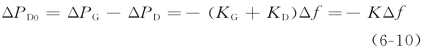
式（6-10）说明系统负荷增加时，在发电机组功频特性和负荷本身的调节效应共同作用下又达到了新的功率平衡。
在式（6-10）中
K称为系统的功率－频率静特性系数，或系统的单位调节功率。它表示在计及发电机组和负荷的调节效应时，引起频率单位变化的负荷变化量。根据K值的大小，可以确定在允许的频率偏移范围内，系统所能承受的负荷变化量。显然，K的数值越大，负荷增减引起的频率变化就越小，频率也就越稳定。
系统中不只一台发电机组时，有些机组可能因已满载，以致调速器受负荷限制器的限制不能再参加调整。这就使系统中总的发电机单位调节功率下降。例如系统中有n台发电机组，n台机组都参加调整时
n台机组中仅有m台参加调整，即第m＋1，m＋2，…，n台机组不参加调整时
显然
如果将KGN和KGM换算为以n台发电机组的总容量为基准的标么值，则这些标么值的倒数就是全系统发电机组的等值调差系统，即
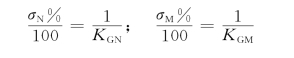
显然
由于上述两方面的原因，使系统中总的发电机单位调节功率从而系统的单位调节功率KS都不可能很大。正因为这样，依靠调速器进行的一次调整只能限制周期较短、幅度较小的负荷变动引起的频率偏移。负荷变动周期更长、幅度更大的调频任务自然地落到了二次调整方面。
【例6-2】设系统中发电机组的容量和它们的调差系数分别为：
水轮机组 100MW/台×5台＝500台MW σ%＝2.5
75MW/台×5台＝375MW σ%＝2.75
汽轮机组 100MW/台×6台＝600MW σ%＝3.5
50MW/台×20台＝1000MW σ%＝4.0
较小容量汽轮机组 合计1000MW σ%＝4.0
系统总负荷为3300MW，负荷的单位调节功率KD＊＝1.5，试计算：（1）全部机组都参加调频；（2）全部机组都不参加调频；（3）仅水轮机组参加调频；（4）仅水轮机组和20台50MW汽轮机组参加调频等四种情况下系统的单位调节功率Ks。计算结果分别以MW/Hz和标么值表示。
解 按
当取KG的基准值KB＝PDN/fN时，KG的标么值为KG*＝
按此二式先计算各类发电机组的KG和KG＊。
5×100MW水轮机组
5×75MW水轮机组
6×100MW汽轮机组
20×50MW汽轮机组
1000MW小容量汽轮机组
系统负荷
而其标么值已知为KD＊＝1.5。
以下求各种不同情况下的KS和KS＊。
（1）所有机组全部参加调频时
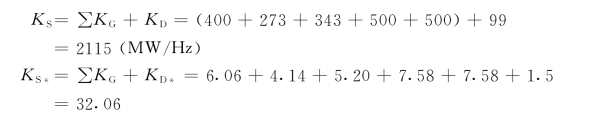
（2）所有机组都不参加调频时
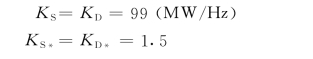
（3）仅水轮机组参加调频时
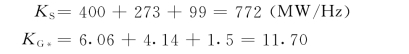
（4）仅水轮机组和20台50MW汽轮机参加调频时
有关电力系统分析的文章
- 详细阅读
-
电力系统中频率的二次调整问题及主调频机组的作详细阅读
若D点固定，则当负荷增加引起转速下降时，由机组调速器自动进行“一次调整”并不能使转速完全恢复。该式也可整理为由上式可见，进行频率的二次调整并不能改变系统的单位调节功率K的数值。在有许多台机组并联运行的电力系统中当负荷变化时，配置了调速器的机组，只要还有可调的容量，都毫无例外地按静态特性参加频率的一次调整。而频率的二次调整一般只是由一台或少数几台发电机组承担，这些机组（厂）称为主调频机组（厂）。......
2023-06-15
-
频率调整：为何必不可少？详细阅读
但是发电机输出的电磁功率是由系统的运行状态决定的，全系统发电机输出的有功功率之和，在任何时刻都是同系统的有功功率负荷相等。第一种变化负荷引起的频率偏移将由发电机组的调速器进行调整。这种调整通常称为频率的一次调整。这一部分负荷将在有功功率平衡的基础上，按照最优化的原则在各发电厂间进行分配。......
2023-06-15
-
电力系统动态频率特性分析详细阅读
电力系统的动态频率特性是指当电力系统由于某种原因，使系统有功功率平衡遭到破坏，系统频率将从额定频率值过渡到频率恢复值所经历的动态过程[11]。目前，当我们研究电力系统频率动态过程以及低频减载方案整定时，为了频率统一变化，分析相对简单，通常采用单机带集中负荷的模型来设计，用多机系统来校验。所以分析简单系统动态频率特性是至关重要的。......
2023-06-29
-
如何判断对数频率的稳定性详细阅读
为了更好地判断其包围点的圈数，在WK平面上定义如下概念。根据正负穿越可将奈氏稳定判据表述如下：对于最小相位系统，P=0，当ω=0→∞，在复平面上WK（jω）正穿越和负穿越次数之差为0时，闭环系统是稳定的，否则闭环系统不稳定；对于非最小相位系统，设系统开环传递函数有P个极点在右半s平面，当ω=0→∞，在复平面上WK（jω）正穿越和负穿越次数之差为P/2时，闭环系统是稳定的，否则闭环系统不稳定。......
2023-06-28
-
如何进行热导率检测？详细阅读
影响涂层热导率的因素很多。温度、显微结构、化学成分、孔隙率等都能显著地改变涂层材料的热导率，属组织敏感参量，目前涂层材料的热导率数值多采用实测的方法获得。由式可知，要想得到热导率λ的值，必须首先知道热扩散率a、比定压热容cp以及密度ρ。λ=acpρ 1.热扩散率的测量方法参照GJB1201.1—1991标准，采用非稳态激光脉冲法进行。......
2023-06-18
-
如何调整导轨副的间隙？详细阅读
还可用多规格的薄垫片来调整导轨的间隙。楔形镶条又称楔铁，楔形镶条的全长厚度斜向变化，长的斜度为1∶100、短的斜度为1∶40，且镶条越长斜度越小；依靠调节螺钉使镶条纵向位移来调整导轨的间隙，调整完毕将其固定；其调整容易且受力均匀，但制造较难。......
2023-06-23
-
如何进行平面旋转？详细阅读
平面的旋转可以解决以下三个作图问题。因此，在平面内作一条投影面平行线进行旋转即可。这要改变平面对V面的倾角，因而应选择铅垂线为旋转轴。图3-63所示为将一般位置平面△ABC旋转成水平面的作图过程：首先把△ABC旋转成正垂面，然后再把正垂面旋转成水平面。......
2023-06-28
相关推荐