首页历史故事系统负荷的有功功率－频率静态特性

系统负荷的有功功率－频率静态特性

2025-09-29 历史故事版权反馈

【摘要】：当系统频率略有下降时，负荷的有功功率成正比例自动减小。图中直线的斜率为或用标么值表示图6-2负荷的有功功率—频率静态特性曲线KD、KD*称为负荷的频率调节效应系数或简称为负荷的频率调节效应。在实际系统中KD*＝1～3，它表示频率变化1%时，负荷有功功率相应变化1%～3%。KD*的数值是调度部门必须掌握的一个数据，因为它是考虑按频率减负荷方案和低频率事故时用一次切除负荷来恢复频率的计算依据。

当频率变化时，系统中的有功功率负荷也将发生变化。系统处于运行稳态时，系统中有功负荷随频率的变化特性称为负荷的静态频率特性。

根据所需的有功功率与频率的关系可将负荷分成以下几种：

（1）与频率变化无关的负荷，如照明、电弧炉、电阻炉和整流负荷等。

（2）与频率的一次方成正比的负荷，负荷的阻力矩等于常数的属于此类，如球磨机、切削机床、往复式水泵、压缩机和卷扬机等。

（3）与频率的二次方成正比的负荷，如变压器中的涡流损耗。

（4）与频率的三次方成正比的负荷，如通风机、静水头阻力不大的循环水泵等。

（5）与频率的更高次方成正比的负荷，如静水头阻力很大的给水泵。

整个系统的负荷功率与频率的关系可以写成

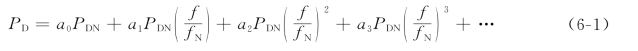
pagenumber_ebook=107,pagenumber_book=100

式中　PD——频率等于f时整个系统的有功负荷；

　　　PDN——频率等于额定值fN时整个系统的有功负荷；

　　　ai——与频率的i次方成正比的负荷占PDN的百分数（i＝0，1，2，…）。

式（6-1）就是电力系统负荷的静态频率特性的数学表达式。若以PDN和fN分别作为功率和频率的基准值，以PDN去除式（6-1）的各项，便得到用标么值表示的功率—频率特性

多项式（6-3）通常只取到频率的三次方为止，因为与频率的更高次方成正比的负荷所占的比重很小，可以忽略。

这种关系可以用曲线来表示，在电力系统运行中，允许频率变化的范围是很小的。在较小的频率变化范围内，这种关系接近一直线。如图6-2所示为电力系统负荷的有功功率—频率静态特性曲线。当系统频率略有下降时，负荷的有功功率成正比例自动减小。图中直线的斜率为(https://www.chuimin.cn)

或用标么值表示

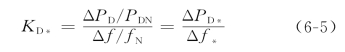
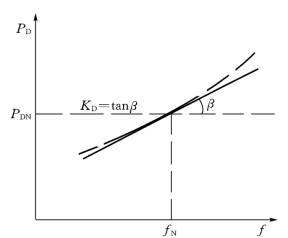
pagenumber_ebook=108,pagenumber_book=101

pagenumber_ebook=108,pagenumber_book=101

图6-2　负荷的有功功率—频率静态特性曲线

KD、KD称为负荷的频率调节效应系数或简称为负荷的频率调节效应。KD的数值取决于全系统各类负荷的比重，不同系统或同一系统不同时节刻KD值都可能不同。

在实际系统中KD＝1～3，它表示频率变化1%时，负荷有功功率相应变化1%～3%。KD的具体数值通常由试验或计算求得。KD的数值是调度部门必须掌握的一个数据，因为它是考虑按频率减负荷方案和低频率事故时用一次切除负荷来恢复频率的计算依据。

【例6-1】某电力系统中，与频率无关的负荷占30%，与频率一次方成正比的负荷占40%，与频率二次方成正比的负荷占10%，与频率三次方成正比的负荷占20%。求系统频率由50Hz降到48Hz和45Hz时，相应的负荷变化百分数。

解　（1）频率降为48Hz时，系统的负荷

pagenumber_ebook=108,pagenumber_book=101

负荷变化为

若用百分值表示便有ΔPD%＝4.7。

（2）频率降为45Hz时，系统的负荷

相应地，ΔPD＝1－0.887＝0.113；ΔPD%＝11.3。