首页历史故事P-Q分解法的计算步骤详解

P-Q分解法的计算步骤详解

2023-06-15 历史故事版权反馈

【摘要】：，n－1）；解修正方程式，求出按修正电压相角；由式求出PQ节点的无功误差及相应的m）；解修正方程式，求出按修正电压值；返回第3步再进行迭代计算，直至满足收敛条件用P—Q分解法对例4-2的电力系统作潮流分布计算。

（1）形成节点导纳矩阵；

（2）给定初值δ（0）、U（0）；

（3）代入式（4-59）和式（4-60）计算节点的有功误差和相应的＝1，2，…，n－1）；

（4）解修正方程式（4-69），求出

（5）按修正电压相角；

（6）由式（4-59）求出PQ节点的无功误差及相应的m）；

（7）解修正方程式（4-70），求出

（8）按修正电压值；

（9）返回第3步再进行迭代计算，直至满足收敛条件

（迭代中的其他问题与牛顿—拉夫逊法相同）

【例4-4】用P—Q分解法对例4-2的电力系统作潮流分布计算。网络参数和给定条件与例4-2的相同。

解　（1）形成有功迭代和无功迭代的简化雅可比矩阵B′和B″，本例直接取用Y阵元素的虚部

pagenumber_ebook=82,pagenumber_book=75

将B′和B″进行三角分解，形成因子表并按上三角存放，对角线位置存放1/dii，非对角线位置存放uij，便得

pagenumber_ebook=83,pagenumber_book=76

（2）给定PQ节点初值和各节点电压相角初值

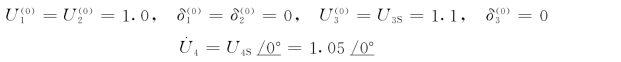
pagenumber_ebook=83,pagenumber_book=76

（3）做第一次有功迭代，按式（4-59）计算节点的有功功率不平衡量

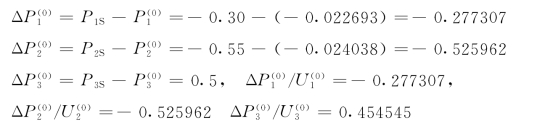
pagenumber_ebook=83,pagenumber_book=76

解修正方程式（4-69）得各节点电压相角修正量为

于是有

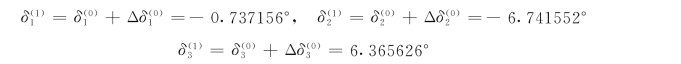
pagenumber_ebook=83,pagenumber_book=76

（4）做第一次无功迭代，按式（4-59）计算节点的无功功率不平衡量，计算时电压相角用最新的修正值。

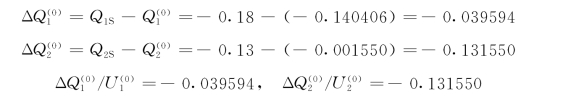
pagenumber_ebook=83,pagenumber_book=76

解修正方程式（4-70），可得各节点电压幅值的修正量为

于是有

到这里为止，第一轮的有功迭代和无功迭代便做完了。接着返回第三步继续计算。迭代过程中节点不平衡功率和电压的变化情况分别列于表4-5和表4-6。

表4-5　节点不平衡功率的变化情况

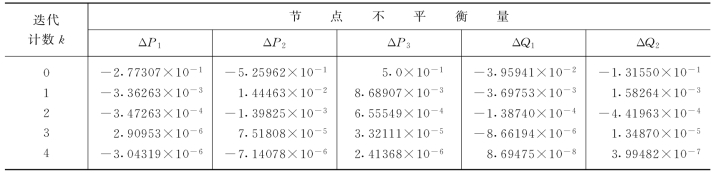
pagenumber_ebook=83,pagenumber_book=76

表4-6　节点电压变化情况

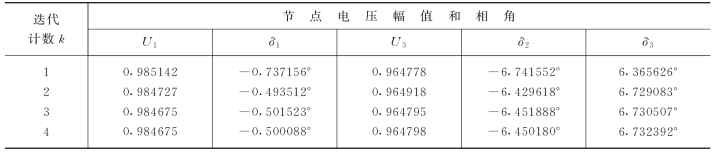
pagenumber_ebook=84,pagenumber_book=77

经过四轮迭代，节点功率不平衡量也下降到10－5以下，迭代到此结束。

与例4-2的计算结果相比较，电压幅值和相角都能够满足计算精度的要求。