迭代过程一直进行到满足收敛判据为止，其中ε1、ε2为预先给定的小正数。牛顿—拉夫逊法的思想是微分学，它将求解非线性方程的问题转化成反复求解一组线性化的修正方程，并对变量进行修正的迭代过程。它同样存在初值选取问题，当初值选取离真解较远时，就失去牛顿—拉夫逊法的成立基础，将对收敛产生影响。......
2023-06-15
牛顿-拉夫逊法在潮流计算中的应用
【摘要】：用牛顿—拉夫逊法进行潮流计算时，节点导纳矩阵的形成、平衡节点和支路功率计算都和运用高斯—塞德尔法时相同，区别仅在于迭代过程。根据式可得式即是用牛顿—拉夫逊法潮流计算时的功率方程。图4-4是牛顿—拉夫逊法潮流计算的流程图。给定值为容许误差ε＝10－5试用牛顿—拉夫逊法计算潮流分布。
用牛顿—拉夫逊法进行潮流计算时，节点导纳矩阵的形成、平衡节点和支路功率计算都和运用高斯—塞德尔法时相同，区别仅在于迭代过程。根据式（4-12）可得
式（4-43）即是用牛顿—拉夫逊法潮流计算时的功率方程。其中
是给定的节点注入功率。
为由节点电压
求得的节点注入功率，二者之差为节点功率的不平衡量。现需要解决的问题是各节点功率的不平衡量都趋近于零时，各节点电压的值应为多少。
由此可见，将式（4-43）与式（4-31）比较可知，式（4-31）中的fi（x1，x2，…，xn）对应式（4-43）中的节点功率不平衡量，而x1，x2，…，xn则对应这里的节点电压。由于牛顿—拉夫逊法解非线性方程组的关键在于求解修正量
则牛顿—拉夫逊法潮流计算的关键是根据功率方程找出其相应的修正方程求解修正量，同时在迭代过程中要根据各节点的不同给定量及各变量的约束条件进行适当处理。
由于节点电压
可表示为两种形式——直角坐标和极坐标形式，下面分别加以叙述。
1.节点电压用直角坐标表示时的牛顿—拉夫逊法潮流计算
采用直角坐标时，节点电压表示为
节点导纳矩阵各元素表示为Yij＝Gij＋jBij。将其代入式（4-43）展开并将实部、虚部分开得
（1）对于PQ节点（i＝1，2，…，m），给定量为节点注入功率，记作Pis，Qis，则节点注入功率的不平衡量为
（2）对于PV节点（i＝m＋1，m＋2，…，n－1），给定量为节点注入有功功率及节点电压的大小，记作Pis，Uis，则电压方程为
因此
即
则式（4-46）中的无功功率误差方程应由电压误差方程代替
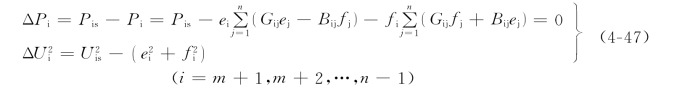
（3）对于平衡节点（i＝n），因为其电压U.n＝en＋jfn给定，故不需迭代求解。
通过以上分析可见，式（4-46）和式（4-47）共2（n－1）个方程，待求变量e1，f1，e2，f2，…，en－1，fn－1共2（n－1）个。将上述2（n－1）个方程按泰勒级数展开，并略去修正量Δei、Δfi的高次方项后得修正方程如下
式中
其中雅可比矩阵的各元素可以对式（4-46）和式（4-47）求偏导数获得。
当i≠j时
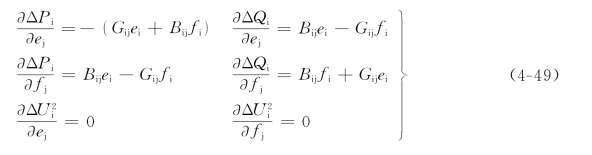
当i＝j时
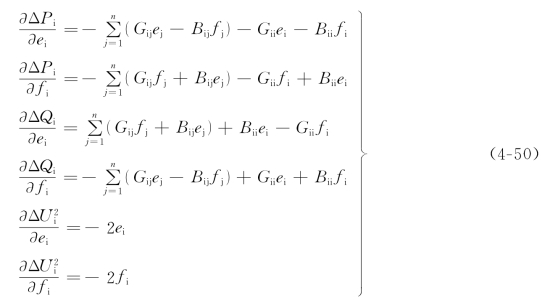
将雅可比矩阵J分块，Jij是2×2阶子阵，误差量ΔW分块为ΔWi，修正量ΔU分块为ΔUi。
对PQ节点
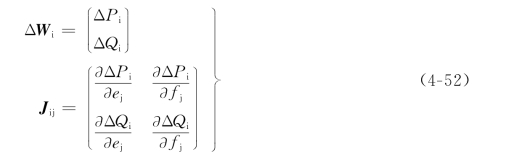
对PV节点
从而式（4-48）可表示为分块矩阵的形式
由式（4-49）、式（4-50）、式（4-52）～式（4-54）可以看出，雅可比矩阵具有以下特点：
（1）雅可比矩阵各元素都是节点电压的函数，它们的数值将在迭代过程中随节点电压的变化而不断变化；
（2）若节点导纳矩阵元素Yij＝Gij＋jBij＝0，则必有Jij＝0。可见，分块形式的雅可比矩阵也是稀疏矩阵，因此修正方程的求解可以应用稀疏矩阵的求解技巧；
（3）雅可比矩阵不具有对称性Jij≠Jji。
图4-4是牛顿—拉夫逊法潮流计算的流程图。
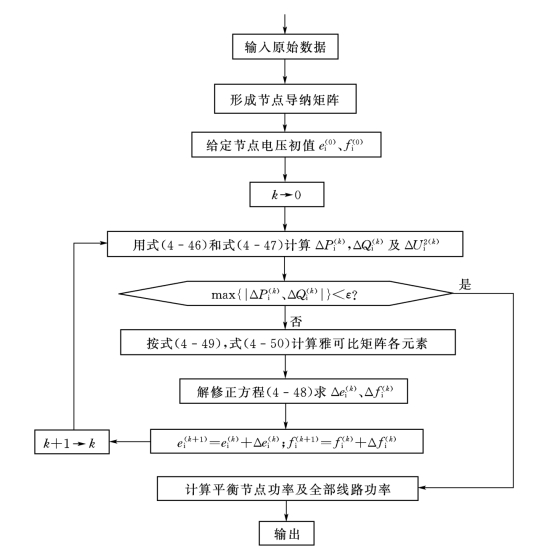
图4-4 牛顿—拉夫逊法潮流计算的流程图
首先，要输入网络的原始数据形成节点导纳矩阵YB，并输入各节点电压的初始值
和
置迭代次数k＝0。然后进入牛顿—拉夫逊法的迭代过程。在进行第k＋1次迭代时，其步骤如下：
（1）按上一次迭代出的节点电压值
利用式（4-46）和式（4-47）计算各类节点的不平衡量
（2）按条件式（4-41）检验收敛，即
ε一般取10－3～10－5即可。如果收敛则迭代结束，利用与高斯—塞德尔法功率计算相同的方法计算功率分布，并输出结果。如不收敛则继续迭代计算。（一般在初值选择合适的情况下，经6～7次迭代即可满足收敛）。
（3）按式（4-49）和式（4-50）计算雅可比矩阵的各元素。
（4）利用式（4-48）解修正量
（5）修正各节点电压
（6）迭代次数加1，进行下一次迭代。
【例4-2】在图4-5所示的电力系统中，网络各元件参数的标么值如下
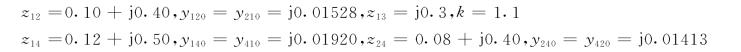
系统中，节点1，2为PQ节点，节点3为PV节点，节点4为平衡节点。给定值为
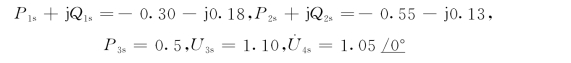
容许误差ε＝10－5试用牛顿—拉夫逊法计算潮流分布。
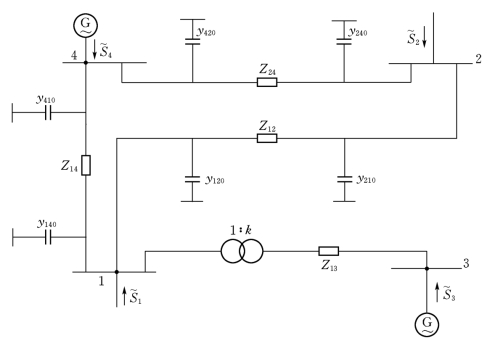
图4-5 例2电力系统结线图
解 （1）按已知网络参数形成节点导纳矩阵如下
（2）给定节点电压初值
（3）按式（4-46）和式（4-47）计算ΔPi、ΔQi和
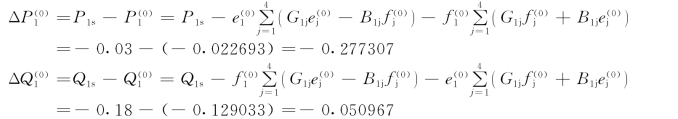
同样的可以算出
根据给定的容许误差ε＝10－5，按式（4-55）校验是否收敛，各节点的不平衡量都未满足收敛条件，于是继续以下计算。
（4）按式（4-49）和式（4-50）计算雅可比矩阵各元素，形成雅可比矩阵，得修正方程式如下
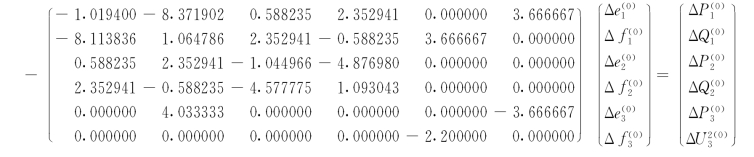
从上述方程中我们看到，每行元素中绝对值最大的都不在对角线上。为了减少计算过程中的舍入误差，可对上述方程进行适当的调整。把第一行和第二行、第三行和第四行、第五行和第六行分别相互对调，便得如下方程
（5）求解修正方程得
（6）按式（4-56）计算节点电压的第一次近似值
这样便结束了一轮迭代。然后返回第三步重复上述计算。做完第三步后即按式（4-55）校验是否收敛，若已收敛，则迭代结束，转入计算平衡节点的功率和线路潮流分布。否则继续做第四、五、六步计算。迭代过程中节点电压和不平衡功率的变化情况分别列于表4-1和表4-2。
表4-1 迭代过程中节点电压变化情况
表4-2 迭代过程中节点不平衡量的变化情况
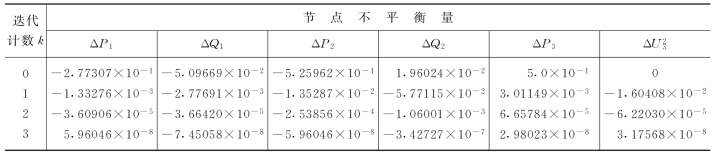
由表中数字可见，经过3次迭代计算即已满足收敛条件。收敛后，节点电压用极坐标表示可得
（7）按式（4-43）计算平衡节点功率，得
线路功率分布的计算结果见例4-3。
2.节点电压用极坐标表示时的牛顿—拉夫逊法潮流计算
节点电压的极坐标形式为
节点导纳矩阵各元素仍为Yij＝Gij＋jBij，将其代入式（4-43）可得
将其实部和虚部分开可得
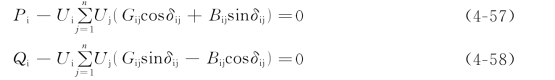
式中 δij＝δi－δj，是节点i、j两节点电压的相角差。在有n个母线的系统中，仍假定1～m号节点为PQ节点；m＋1～n－1号节点为PV节点；节点n为平衡节点。
（1）对PQ节点，Pis和Qis已知，未知量为Ui和δi。节点功率的不平衡量为
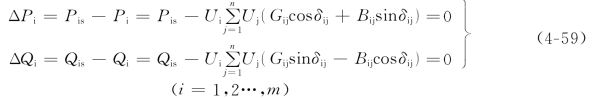
（2）对PV节点，Pis和Uis给定，Qi、δi未知，此时ΔQi方程失去作用，ΔPi方程为
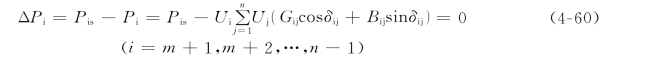
（3）对平衡节点n，电压Un、δn已知，不用迭代计算。
由以上分析可见，式（4-59）和式（4-60）共有（n－1＋m）个方程，未知量为Ui（i＝1，2，…，m）和δi（i＝1，2，…，n－1），共有（m＋n－1）个，与方程数相同，因此方程可解。将上述（n－1＋m）个方程按泰勒级数展开，略去修正量Δδi、ΔUi的二次方及以上的高次方项，可得如下形式的修正方程
式中为了使H、N、K、L的表达式有相似的结构，电压的修正量用ΔUi/Ui形式代替。
雅可比矩阵各元素如下：
将式（4-61）简写成分块矩阵的形式
其中H为（n－1）阶方阵，L为m阶方阵，N为（n－1）×m阶矩阵，K为m×（n－1）阶矩阵。
计算的步骤和流程图与直角坐标形式类似。需指出的是，由于PV节点可能向PQ节点转化，修正方程式的结构不是一成不变的。在PV节点因无功功率越限而向PQ节点转化时，修正方程式中相应的行也随之转化。采用直角坐标时，应以对应于该节点无功功率不平衡量
的关系式取代原来对应于该节点电压不平衡量
的表达式。采用极坐标时，应增加一个对应于该节点无功功率不平衡量
的关系式，当
【例4-3】节点电压用极坐标表示，对例4-2的电力系统作牛顿法潮流计算。网络参数和给定条件同例4-2。
解 节点导纳矩阵与例4-2的相同。
（1）给定节点电压初值
（2）利用式（4-59）和式（4-60）计算节点功率的不平衡量，得
（3）用式（4-62）计算雅可比矩阵各元素，可得
（4）求解修正方程式（4-63）得节点电压的修正量为
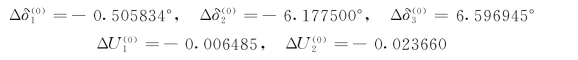
对节点电压进行修正
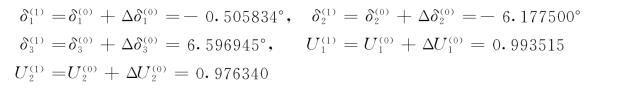
然后返回第二步作下一轮的迭代计算。取ε＝10－5，经过三次迭代，即满足收敛条件。迭代过程中节点功率不平衡量和电压的变化情况列于表4-3和表4-4。
表4-3 节点功率不平衡量的变化情况
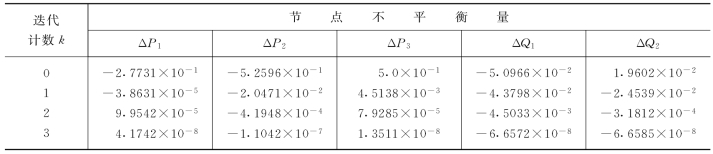
表4-4 节点电压的变化情况
节点电压的计算结果同例4-2的结果是吻合的。迭代的次数相同，也是三次。
（5）按式（4-43）计算平衡节点的功率
按式（4-28）计算全部线路功率，结果如下
有关电力系统分析的文章
- 详细阅读
-
对称分量法在不对称短路计算中的应用详细阅读
现以图11-3所示简单电力系统为例来说明应用对称分量法计算不对称短路的一般原理。应用对称分量法将这组不对称电势源分解成正序、负序和零序三组对称分量，如图11-4所示。它说明了各种不对称短路时各序电流和同一序电压间的相互联系，表示了不对称短路的共性。根据不对称短路的类型可以得到三个说明短路性质的补充条件，它们表示了各种不对称短路的特性，通常称为故障条件或边界条件。......
2023-06-15
-
离散求和法在水文分析计算和水资源评价中的应用详细阅读
图7.4频率曲线离散化示意图7.3.2.1计算方法设计断面以上有单一水库的情况。离散后，X与Y都只能取有限个状态值。Z的相应状态对应的概率区间为ΔPZ，ij。......
2023-08-23
-
连续型潮流计算的方法及应用详细阅读
首先介绍纯交流系统连续型潮流计算方法的原理和步骤[1～3]。图5.1所示为连续型潮流计算法的示意图，该算法主要有4个步骤：参数化、预测、校正及步长控制。......
2023-06-29
-
高斯-塞德尔法潮流计算方法详解详细阅读
应用高斯—塞德尔法进行潮流计算的步骤如下：根据网络结构和参数形成节点导纳矩阵YB；迭代计算各节点电压对PQ节点的处理（i＝1，2，…，n－1）是已知的，因此PV节点的电压初值取为并且在每次迭代完均要修正，具体方法见PV节点。这一迭代过程一直进行到满足收敛条件为止。因为PV节点已知的是Pi、Ui，所以迭代初值应设为然后应用式进行计算，并且作如下修正：a.修正节点电压。......
2023-06-15
-
臭氧氧化法在废水处理中的应用详细阅读
臭氧氧化法在废水处理中主要是使污染物氧化分解，用于降低BOD、COD，脱色、除臭、除味，杀菌、杀藻，除铁、锰、氰、酚等，现举例如下。废水经生物处理后进行臭氧氧化法脱色处理。印染废水的色度，特别是水溶性染料，用一般方法难于脱色，采用臭氧氧化法可得到较高的脱色率，设备虽复杂，但废水处理后没有一次有害物质产生。......
2023-06-19
-
云计算技术在计算机应用基础教程中的应用详细阅读
由于云计算需要对海量的分布式数据进行处理、分析，因此，数据管理技术必须能够高效地管理大量的数据。全球各大云计算方案/服务提供商们都在积极开展相关技术的研发工作。......
2023-11-23
-
计算机在控制中的应用方式介绍详细阅读
根据计算机在控制中的应用方式，可以把计算机控制系统划分为4类：操作指导控制系统、直接数字控制系统、监督计算机控制系统和分级计算机控制系统。监督计算机控制系统构成示意如图5－10所示。当SCC计算机发生故障时，可由模拟调节器独立执行控制任务。SCC计算机完成工段、车间等高一级的最优化分析和计算，然后给出最优设定值，送给DDC计算机执行控制。分级计算机控制系统生产过程中既存在控制问题，也存在大量的管理问题。......
2023-06-23
相关推荐