牛顿拉夫逊法的基本原理及应用

2023-06-15 历史故事版权反馈

【摘要】：迭代过程一直进行到满足收敛判据为止，其中ε1、ε2为预先给定的小正数。牛顿—拉夫逊法的思想是微分学，它将求解非线性方程的问题转化成反复求解一组线性化的修正方程，并对变量进行修正的迭代过程。它同样存在初值选取问题，当初值选取离真解较远时，就失去牛顿—拉夫逊法的成立基础，将对收敛产生影响。

设有非线性方程组如下

其近似解为设近似解与精确解分别相差

将上式中每一式都按泰勒级数展开，以第i式为例可得

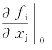其中Φi是包含Δxj（j＝1，2，…，n）的高次方与fi的高阶偏导数乘积的函数。如近似解与精确解相差不大，则Δxj的高次方可以略去，从而Φi可略去。另 pagenumber_ebook=70,pagenumber_book=63 代表函数fi对自变量xj的偏导数在点的值（j＝1，2，…，n）。由此可得

将上式写成矩阵形式

简写为

这是一个关于修正量的线性方程组，式中f为误差列向量；J称为函数fi的雅可比矩阵；Δx为由Δxj组成的修正列向量。因此可解得修正量Δxj（j＝1，2，…，n）。

对初值进行修正

此时并不是方程组的真解，而是向真解xj逼近了一步。可反复进行迭代、修正。其迭代用的修正方程为

其中k为迭代次数，解出修正量对各变量再进行修正

设是由n个多元函数组成的n维误差列相量，则式（4-37）和式（4-38）可缩写为

J（k）为第k次迭代的雅可比矩阵。

迭代过程一直进行到满足收敛判据

为止，其中ε1、ε2为预先给定的小正数。此过程即是求解误差量fx（（k））趋近于零时的x相量。

牛顿—拉夫逊法的思想是微分学，它将求解非线性方程的问题转化成反复求解一组线性化的修正方程，并对变量进行修正的迭代过程。在迭代过程中，误差量fx（（k））和雅可比矩阵J（k），每迭代一次都需重新计算一次。它同样存在初值选取问题，当初值选取离真解较远时，就失去牛顿—拉夫逊法的成立基础，将对收敛产生影响。

牛顿拉夫逊法的基本原理及应用

相关推荐