首页历史故事功率方程的展开与平衡关系分析

功率方程的展开与平衡关系分析

2025-09-29 历史故事版权反馈

【摘要】：参照式（4-1），将展开可得功率方程的一般形式为1.功率方程的展开式以下面两端供电网络为例，分析功率方程的展开式。将式的第一、二式相加，第三、四式相加，可得这个系统的有功功率、无功功率平衡关系为两等式右边第三项、第四项为系统的有功功率损耗ΔP、无功功率损耗ΔQ在功率方程中，母线电压的相位角以δ12＝δ1－δ2的形式出现，即决定功率大小的是相对角而不是绝对角，因此在所有电压相量U.i中，应选定一个电压参考相量。

前面已知节点电压方程为IB＝YBUB。在建立了节点导纳矩阵YB后，如UB或IB已知，则方程可解。由第三章可知，在工程计算中IB是未知的，UB中的元素大多数也未知，因此无法直接应用公式（4-1）进行求解。电力系统分析计算中常以节点注入功率SB代替电流IB（SB为节点注入功率的列相量）。根据复功率的定义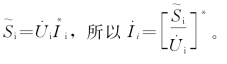 pagenumber_ebook=63,pagenumber_book=56 对应有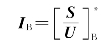^[1]，所以节点电压方程为从而将各节点的注入功率引入了节点电压方程。参照式（4-1），将展开可得功率方程的一般形式为

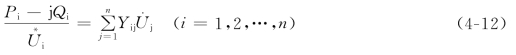
pagenumber_ebook=63,pagenumber_book=56

1.功率方程的展开式

以下面两端供电网络为例，分析功率方程的展开式。如图4-2所示两端供电网络，节点1、2的注入功率为

pagenumber_ebook=63,pagenumber_book=56

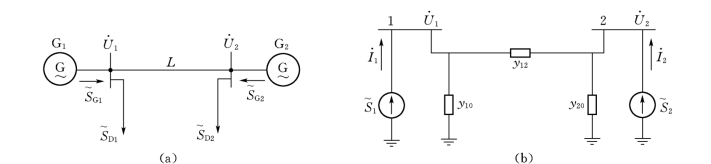
pagenumber_ebook=64,pagenumber_book=57

图4-2　简单系统及其等值网络

（a）简单系统；（b）等值网络

从而可知节点1、2的注入电流为

pagenumber_ebook=64,pagenumber_book=57

网络的节点导纳矩阵元素

从而网络的节点电压方程为

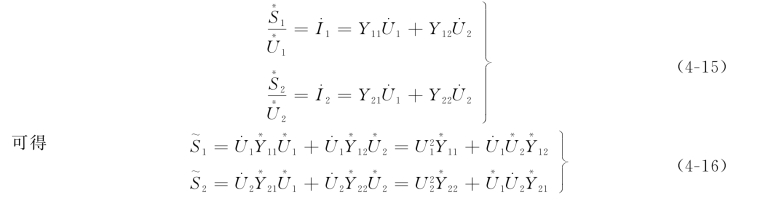
pagenumber_ebook=64,pagenumber_book=57

如设（均为极坐标形式），并将它们代入式（4-16）展开，将有功功率、无功功率分别列出，可得(https://www.chuimin.cn)

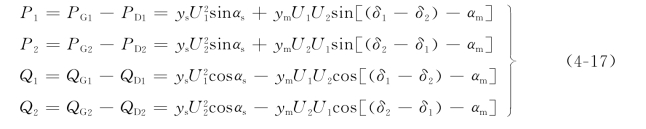
pagenumber_ebook=64,pagenumber_book=57

这就是图4-2（a）简单系统的功率方程。

2.功率方程的特点

（1）由式（4-17）可见，功率方程是反应节点注入功率和节点电压之间关系的数学模型，是关于U和δ的非线性方程组，一般无法用解析法求解，应立足于迭代求解。

（2）将式（4-17）的第一、二式相加，第三、四式相加，可得这个系统的有功功率、无功功率平衡关系为

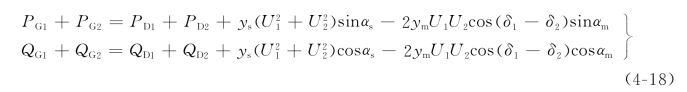
pagenumber_ebook=65,pagenumber_book=58

两等式右边第三项、第四项为系统的有功功率损耗ΔP、无功功率损耗ΔQ

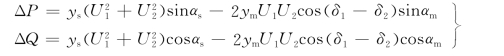
pagenumber_ebook=65,pagenumber_book=58

（3）在功率方程中，母线电压的相位角以δ12＝δ1－δ2的形式出现，即决定功率大小的是相对角而不是绝对角，因此在所有电压相量U.i中，应选定一个电压参考相量。

（4）四个方程中，除去网络参数ys、ym、αs、αm外共十二个变量，它们分别是：

负荷消耗的有功、无功功率——PD1、PD2、QD1、QD2；

电源发出的有功、无功功率——PG1、PG2、QG1、QG2；

母线或节点电压的大小和相位角——U1、U2、δ1、δ2。

因此，除非已知或给定其中的八个变量，否则无法求解，即为n母线系统将会列出2n个方程，但变量有6n个。必须根据运行条件，给定其中6n－2n＝4n个变量才可解方程。