本文拟从马克思对自己思想发展的回忆和论述的最直接材料出发，来阐明其唯物史观形成的起点和《手稿》在这个形成过程中的关键地位。......
2024-01-10
节点导纳矩阵的形成与修改
【摘要】：用节电导纳矩阵描述的节点电压方程是依靠节点导纳矩阵来建立节点电流与节点电压之间关系的，因此须先确定节点导纳矩阵。在复杂电力网中，这种情况较多，从而使矩阵中出现大量的零元素，节点导纳矩阵成为稀疏矩阵。因此，节点导纳矩阵是一个对称、稀疏且具有对角线优势的方阵。
用节电导纳矩阵描述的节点电压方程是依靠节点导纳矩阵来建立节点电流与节点电压之间关系的，因此须先确定节点导纳矩阵。
1.节点导纳矩阵的形成
节点导纳矩阵如式（4-2）。其中对角元素Yii（i＝1，2，…，n）称为节点i的自导纳；非对角元素Yij（i，j＝1，2，…，n；i≠j）称为互导纳。
（1）自导纳Yii。将式（4-1）展开得
若在节点i加电压
其他节点都接地，即
（k＝1，2，…，n，k≠i），则
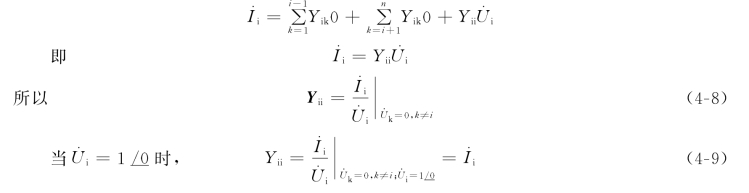
所以自导纳Yii的物理意义是：在节点i施加单位电压，其他节点都接地时，经节点i注入网络的电流。实际计算中，由电路原理课程已知，节点i的自导纳在数值上就等于与该节点直接相连的所有支路导纳的总和。
（2）互导纳Yij。若在节点j加电压
其他节点都接地，即
k≠j），由式（4-7）可知
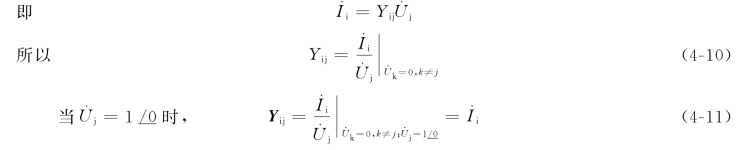
因此，互导纳Yij的物理意义是：在节点j施加单位电压，其他节点都接地时，经节点i注入网络的电流。实际计算中，节点i、j之间的互导纳Yij在数值上就等于连接节点i与j的支路导纳yij的负值。取负号的原因是节点注入网络的电流为正，而当i接地且
时，
的方向为流出网络（即注入大地）。
依互导纳的物理意义可知Yij＝－yij，即Yij＝Yji；特别地，当节点i、j之间无直接支路相连时，Yij＝Yji＝0。在复杂电力网中，这种情况较多，从而使矩阵中出现大量的零元素，节点导纳矩阵成为稀疏矩阵。一般来说
即对角元素的绝对值大于非对角元素的绝对值，使节点导纳矩阵成为具有对角线优势的矩阵。因此，节点导纳矩阵是一个对称、稀疏且具有对角线优势的方阵。这将给以后的分析计算带来很大的方便，它有利于节省内存、提高计算速度以及改善收敛等。
2.节点导纳矩阵的修改
在电力系统中，接线方式或运行状态等均会发生变化，从而使网络接线改变。比如一台变压器支路的投入或切除，均会使与之相连的节点的自导纳或互导纳发生变化，而网络中其他部分的结构并没改变，因此不必重新形成节点导纳矩阵，而只需对原有的矩阵作必要的修改就可以了。现就几种典型的接线变化说明具体的修改方法。
（1）从原有网络的节点i引出一条导纳为Yij的支路，j为新增点的节点，如图4-1（a）所示。由于新增加了一个节点，所以节点导纳矩阵增加一阶，矩阵作如下修改：
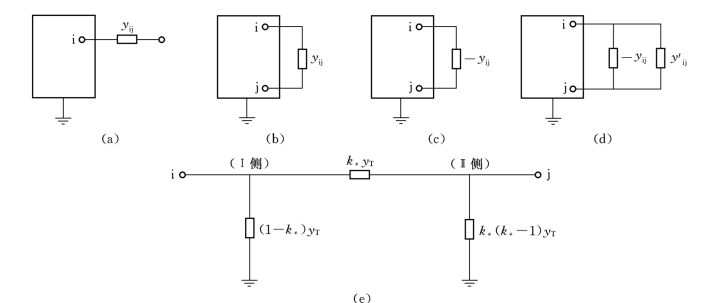
图4-1 电力网络接线的改变
（a）增加支路和节点；（b）增加支路；（c）切除支路；（d）改变支路参数；（e）改变变压器变比
1）原有节点i的自导纳Yii的增量ΔYii＝yij；
2）新增节点j的自导纳Yjj＝yij；
3）新增的非对角元Yij＝Yji＝－yij；其他新增的非对角元均为零。
（2）在原有网络的节点i与j之间增加一条导纳为yij的支路，如图4-1（b）所示。则与i、j有关的元素应作如下修改：
1）节点i、j的自导纳增量ΔYii＝ΔYjj＝yij；
2）节点i与j之间的互导纳增量ΔYij＝ΔYji＝－yij。
（3）在网络的原有节点i、j之间切除一条导纳为yij的支路，如图4-1（c）所示，其相当于在i、j之间增加一条导纳为－yij的支路，因此与i、j有关的元素应作如下修改：
1）节点i、j的自导纳增量ΔYii＝ΔYjj＝－yij；
2）节点i与j之间的互导纳增量ΔYij＝ΔYji＝yij。
（4）原有网络节点i、j之间的导纳由yij改变为y′ij，相当于在节点i、j之间切除一条导纳为yij的支路，再增加一条导纳为y′ij的支路，如图4-1（d）所示。则与i、j有关的元素应作如下修改：
1）节点i、j的自导纳增量ΔYii＝ΔYjj＝y′ij－yij；
2）节点i与j之间的互导纳增量ΔYij＝ΔYji＝yij－y′ij。
（5）原有网络节点i、j之间变压器的变比由k*变为k′*，即相当于切除一台变比为k*的变压器，再投入一台变比为k′*的变压器，k*＝（UⅠ/UⅡ）/（UⅠB/UⅡB），如图4-1（e）变压器Π型等值电路，图中yT为与变压器原边基准电压对应的变压器导纳标么值，则与i、j有关的元素应作如下修改：
1）节点i的自导纳增量ΔYii＝0；节点j的自导纳增量
2）节点i与j之间的互导纳增量ΔYij＝ΔYji＝（k*－k′*）yT。
有关电力系统分析的文章
- 详细阅读
-
矩阵初等变换、初等矩阵与等价矩阵解析详细阅读
【主要内容】1.矩阵的初等变换矩阵的下列三种变换称为矩阵的初等行（列）变换：（1）互换矩阵的两行（两列）.（2）用一个非零常数c乘矩阵的某行（某列），即用c乘某行（某列）的每个元素.（3）矩阵某行（某列）的k倍加到另一行（另一列），即某行（某列）的每个元素的k倍，加到另一行（另一列）的对应元素.矩阵的初等行变换与初等列变换，总称矩阵的初等变换.2.初等矩阵单位矩阵经过一次初等变换所得到的矩阵，称为......
2023-10-27
-
修改建议：改为修改短文的技巧与要点详细阅读
题目要求阅读下面短文，根据你的理解和感受，试着修改润色这篇习作。写作提示1.仔细阅读文章，发现其长处与不足，不足之处就是需要修改的地方。(金诗雨)教师评语小作者从“言”和“意”两个方面对原文进行了修改润色。......
2023-07-05
- 详细阅读
-
线性代数9讲-实对称矩阵与正交矩阵详细阅读
（1）若A为实对称矩阵，则①特征值均为实数，特征向量均为实向量.②不同特征值对应的特征向量正交.（即λ1≠λ2ξ1⊥ξ2（ξ1，ξ2）＝0，建方程）③可用正交矩阵相似对角化.（即存在正交矩阵P，使P－1AP＝PTAP＝Λ）见例8.12至例8.15.（2）若A为正交矩阵，则ATA＝EA－1＝ATA由规范正交基组成AT是正交矩阵A－1是正交矩阵A*是正交矩阵－A是正交矩阵.（3）若A，B为同阶正交矩阵......
2023-11-21
-
矩阵运算与分块矩阵简明指南详细阅读
，n）排成的m行n列的矩形表称为m×n矩阵，aij称为A的第i行第j列的元素（i=1，2，…，As都是方阵），则，|A|=|A1||A2|…，n.于是将式代入式得|A+B|=2n-1，即21-n|A+B|=|A|+|B|.例5.3.3 设n阶矩阵A，B，C满足AB=BC=CA=En，求A2+B2+C2.精解 由AB=BC=CA=En得A2=AEnA=AA==E2n=En，B2=BEnB=BB==E2n=En，C2=CEnC=CC==E2n=En，所以，A2+B2+C2=En+En+En=3En.例5.3.4 设n阶矩阵A，B满足ATA=AAT=En，BTB=BBT=En，且|A|=-|B|，证明：|A+B|=0.精解 由题设知，|A+B|=|EnA+BEn|=|BBTA+BATA|=|B||BT+AT||A|=-|A|2|（A+B）T|=-|A|2|A+B|，即|A+B|=0.由此推出|A+B|=0.......
2023-10-27
-
程序输入与修改的方法优化建议：如何输入和修改详细阅读
7）重复以上步骤5）、6），完成全部程序的输入。2）利用第8章所述的CNC参数设定操作，将图7.3-1所示的CNC设定参数页面上的“顺序号”设定为“1”，生效程序段号自动插入功能。图7.3-2 程序段号的自动生成3.字的编辑加工程序中的程序字可通过插入、替换、删除等操作进行编辑。......
2023-06-25
-
节点数量、节点自由度限制和节点连通度需求对算详细阅读
图6-4给出了3种仿真场景下算法得到的最重拓扑，图，，表示3种仿真场景中运行DMST算法得到的近似最优的最小生成树，图，，表示对应的CG算法的结果。在仿真中，仅考虑RC中的可行解来与CG算法比较。图6-7给出了两种算法在3种仿真场景中的运算结果。......
2023-07-02
相关推荐